"2016학년도 대학수학능력시험 수학 B형 29번"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| 82번째 줄: | 82번째 줄: | ||
==내적의 최대값 찾기== | ==내적의 최대값 찾기== | ||
| + | 매스매티카의 명령어 NMaximize를 이용하면, $0\leq t\leq 2\pi,0\leq u\leq 2\pi,0\leq v\leq\pi$일 때, 3변수 함수 $\overrightarrow{AP(t)}\cdot\overrightarrow{AQ(u,v)}$의 최대값이 얼마인지를 찾을 수 있는데, 이는 3.1861406616345071649626528670547323295550661144957 | ||
| + | 이다. | ||
| + | 이는 위에서 실행한 실험의 결과에 부합한다. 따라서 이제 $\overrightarrow{AP}\cdot\overrightarrow{AQ}$의 최대값에 대한 확신을 가질 수 있다. | ||
| + | |||
| + | |||
| + | ==PSLQ 알고리즘의 적용== | ||
| + | 이제 위에서 얻은 값을 $\alpha=3.1861406616345071649626528670547323295550661144957$라 두자. | ||
| + | |||
| + | 문제에서는 $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 최댓값이 $a+b\sqrt{33}, a,b\in \mathbb{Q}$꼴이라고 하였으므로, 만약에 $a+b\sqrt{33}=\alpha$의 관계가 성립한다면, | ||
| + | 적당한 정수 $p,q,r$가 존재하여 $p+q \sqrt{33}+r \alpha=0$이 성립해야 한다. | ||
| + | |||
| + | 이러한 상황에서 유용한 실험수학의 알고리즘이 바로 [[PSLQ 알고리즘]]이다. 이는 주어진 여러개의 실수 사이에 정수 계수를 이용한 선형 관계가 존재하는지를 찾는데 이용된다. PSLQ 알고리즘을 적용하면, $(p,q,r)=(7,1,-4)$를 얻는다. 즉 $7+\sqrt{33}-4 \alpha=0$가 성립할 개연성이 높다는 것이다. | ||
| + | |||
| + | 따라서 $(a,b)=(7,1)/4$이고, 문제의 답은 50이 된다. | ||
| + | |||
| + | 참고로, 이렇게 내적의 값을 최대로 만드는 $P$와 $Q$의 위치는 다음과 같다 | ||
| + | $$ | ||
| + | \begin{aligned} | ||
| + | P & =\left(\frac{7}{4}-\frac{7}{4 \sqrt{33}},\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{66}},\frac{5 \sqrt{3}}{4}-\frac{5}{4 \sqrt{11}}\right) \\ | ||
| + | Q & =\left(-\frac{1}{4}-\frac{7}{4 \sqrt{33}},-\sqrt{\frac{17}{33}+\frac{1}{\sqrt{33}}},\frac{\sqrt{3}}{4}-\frac{5}{4 \sqrt{11}}\right) | ||
| + | \end{aligned} | ||
| + | $$ | ||
[[파일:2016학년도 대학수학능력시험 수학 B형 29번3.gif]] | [[파일:2016학년도 대학수학능력시험 수학 B형 29번3.gif]] | ||
| + | |||
| + | |||
| + | |||
| + | ==매스매티카 파일 및 계산 리소스== | ||
| + | * https://drive.google.com/file/d/0B8XXo8Tve1cxWlJ3R2tpbDNJOEU/view | ||
2015년 11월 13일 (금) 21:13 판
개요
- 2016학년도 대학수학능력시험 수학 B형 29번 문제에 대하여, 실험수학 (experimental mathematics) 적 접근을 시도함
- 경험과학으로서의 수학을 소개하는 에세이
- 문제풀이의 4단계 전략
- 매개화를 이용하여 문제를 실험이 가능한 형태로 만들기
- 임의 추출을 이용한 실험을 수행하여 근사값 찾기
- 이를 이용하여 더 정확한 근사값을 찾아냄
- PSLQ 알고리즘을 적용하여 정확한 답을 찾기
문제의 이해
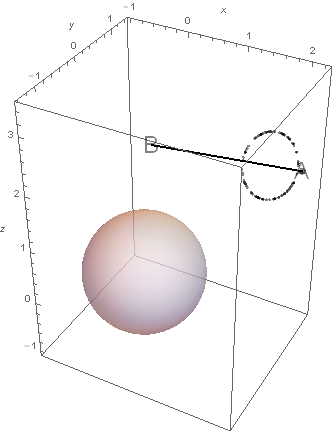
주어진 문제는 다음과 같다
좌표공간의 두 점 $A(2,\sqrt{2},\sqrt{3})$ , $B(1,-\sqrt{2},2 \sqrt{3})$ 에 대하여 점 $P$ 는 다음 조건을 만족시킨다.
(가) $|\overrightarrow{AB}|=1$
(나) $\overrightarrow{AP}$와 $\overrightarrow{AB}$가 이루는 각의 크기는 $\frac{\pi}{6}$이다.
중심이 원점이고 반지름의 길이가 1인 구 위의 점 $Q$에 대하여 $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 최댓값이 $a+b\sqrt{33}$이다. $16(a^2+b^2)$의 값을 구하시오. (단, $a,b$는 유리수이다.)
문제의 조건을 만족시키는 점 $P$는 위 그림의 원위에, $Q$는 단위구면 위에 놓여 있다. 이러한 조건 위에서 $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 값을 최대로 만드려 한다.
여기서는 $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 최대값을 찾기 위해서, $P$와 $Q$를 임의로 뽑아내가면서, 그 값이 얼마나 커질 수 있는지에 대한 실험을 수행할 것이다.
원과 구면의 매개화
실험을 수행하기 위해서 $P$와 $Q$가 놓인 원과 구면을 매개화하자.
벡터의 내적과 외적에 대한 계산을 성실하게 수행하면 (물론 컴퓨터가 했다), $P$는 다음과 같은 원위에 놓여 있음을 알 수 있다. $$ \mathbf{P}(t):=\left(\sqrt{\frac{3}{22}} \sin (t)+\frac{7 \cos (t)}{4 \sqrt{33}}+\frac{7}{4},-\frac{1}{2} \sqrt{\frac{3}{11}} \sin (t)+\frac{\cos (t)}{\sqrt{66}}+\frac{1}{\sqrt{2}},\frac{1}{44} \left(-2 \sqrt{22} \sin (t)+5 \sqrt{11} \cos (t)+55 \sqrt{3}\right) \right),\quad 0\leq t\leq 2\pi \label{PP} $$
단위구면은 구면좌표계를 이용하여 매개화할 수 있다. $$ \mathbf{Q}(u,v):=\left(\cos u \sin v, \sin u \sin v, \cos v \right),\quad 0\leq u\leq 2\pi,0\leq v\leq\pi \label{QQ} $$
임의 추출을 이용한 실험
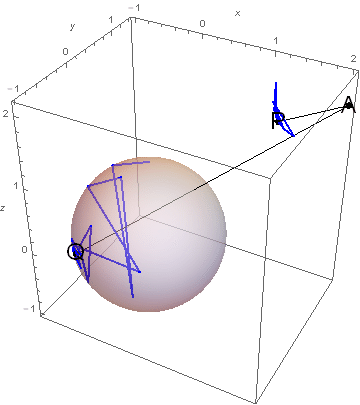
이제 컴퓨터를 이용하여 $0\leq t\leq 2\pi,0\leq u\leq 2\pi,0\leq v\leq\pi$를 만족하는 $(t,u,v)$를 임의로 뽑아낸 뒤, \ref{PP}와 \ref{QQ}를 이용하여, $P=\mathbf{P}(t)$와 $Q=\mathbf{Q}(u,v)$를 구하고, $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 값을 구하자.
이를 백만번 시행하면서 전보다 더 큰 $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 값이 얻어질 때마다 이를 기록하자. 아래는 $n$번째 임의 추출에서 얻은 값 $\overrightarrow{AP}\cdot \overrightarrow{AQ}$과 $(t,u,v)$의 표이다.
$$ \begin{array}{c|c|c} n & \overrightarrow{AP}\cdot \overrightarrow{AQ} & (t,u,v) \\ \hline 1 & 1.90334 & \{3.30047,2.08294,0.964364\} \\ 7 & 2.22899 & \{4.09651,2.8632,0.706553\} \\ 10 & 2.26728 & \{3.43351,4.16351,2.86169\} \\ 12 & 2.56336 & \{3.46444,3.90584,0.325815\} \\ 37 & 2.69629 & \{2.94468,3.36154,0.925869\} \\ 44 & 2.75229 & \{2.92377,5.14198,1.36891\} \\ 55 & 2.77746 & \{3.65922,3.5053,1.8994\} \\ 120 & 2.79647 & \{2.57083,4.29973,1.00076\} \\ 134 & 2.99473 & \{2.90661,4.08459,2.09397\} \\ 432 & 3.15013 & \{3.28658,4.25869,1.42484\} \\ 680 & 3.16119 & \{3.19468,3.89187,1.44537\} \\ 6695 & 3.17031 & \{3.08166,4.22474,1.6721\} \\ 9331 & 3.17362 & \{3.2183,3.98487,1.57295\} \\ 25934 & 3.17667 & \{3.19106,3.98259,1.54103\} \\ 67319 & 3.17772 & \{3.10662,4.02173,1.48524\} \\ 82935 & 3.18138 & \{3.06238,4.17261,1.51169\} \\ 160703 & 3.18452 & \{3.11131,4.16613,1.48792\} \\ 266823 & 3.18483 & \{3.16744,4.1446,1.53316\} \\ 353596 & 3.18553 & \{3.14674,4.10179,1.4851\} \\ 556290 & 3.18614 & \{3.14195,4.12252,1.51449\} \\ \end{array} $$
표에 해당하는 $P$와 $Q$의 위치가 어떻게 변하는지를 아래의 그림에서 관찰할 수 있다.
이 실험이 말해주는 것은 분명하다. $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 값을 최대로 만드는 쌍 $(P,Q)$는 유일하게 존재하며, $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 값은 3.18 언저리이다.
내적의 최대값 찾기
매스매티카의 명령어 NMaximize를 이용하면, $0\leq t\leq 2\pi,0\leq u\leq 2\pi,0\leq v\leq\pi$일 때, 3변수 함수 $\overrightarrow{AP(t)}\cdot\overrightarrow{AQ(u,v)}$의 최대값이 얼마인지를 찾을 수 있는데, 이는 3.1861406616345071649626528670547323295550661144957 이다.
이는 위에서 실행한 실험의 결과에 부합한다. 따라서 이제 $\overrightarrow{AP}\cdot\overrightarrow{AQ}$의 최대값에 대한 확신을 가질 수 있다.
PSLQ 알고리즘의 적용
이제 위에서 얻은 값을 $\alpha=3.1861406616345071649626528670547323295550661144957$라 두자.
문제에서는 $\overrightarrow{AP}\cdot \overrightarrow{AQ}$의 최댓값이 $a+b\sqrt{33}, a,b\in \mathbb{Q}$꼴이라고 하였으므로, 만약에 $a+b\sqrt{33}=\alpha$의 관계가 성립한다면, 적당한 정수 $p,q,r$가 존재하여 $p+q \sqrt{33}+r \alpha=0$이 성립해야 한다.
이러한 상황에서 유용한 실험수학의 알고리즘이 바로 PSLQ 알고리즘이다. 이는 주어진 여러개의 실수 사이에 정수 계수를 이용한 선형 관계가 존재하는지를 찾는데 이용된다. PSLQ 알고리즘을 적용하면, $(p,q,r)=(7,1,-4)$를 얻는다. 즉 $7+\sqrt{33}-4 \alpha=0$가 성립할 개연성이 높다는 것이다.
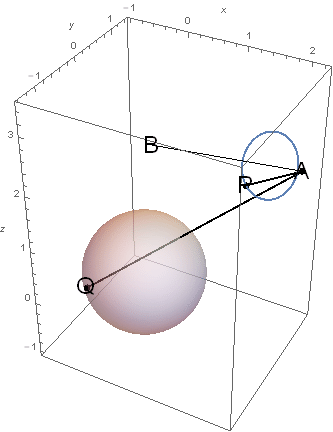
따라서 $(a,b)=(7,1)/4$이고, 문제의 답은 50이 된다.
참고로, 이렇게 내적의 값을 최대로 만드는 $P$와 $Q$의 위치는 다음과 같다 $$ \begin{aligned} P & =\left(\frac{7}{4}-\frac{7}{4 \sqrt{33}},\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{66}},\frac{5 \sqrt{3}}{4}-\frac{5}{4 \sqrt{11}}\right) \\ Q & =\left(-\frac{1}{4}-\frac{7}{4 \sqrt{33}},-\sqrt{\frac{17}{33}+\frac{1}{\sqrt{33}}},\frac{\sqrt{3}}{4}-\frac{5}{4 \sqrt{11}}\right) \end{aligned} $$