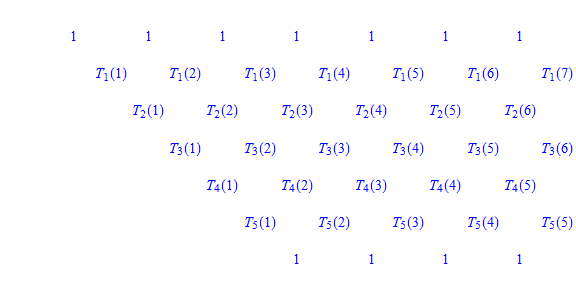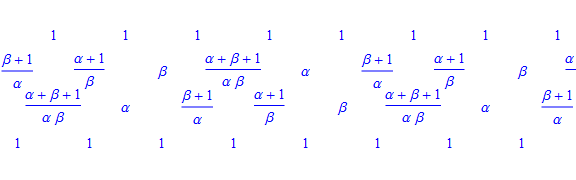"콕세터 프리즈"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
 
(같은 사용자의 중간 판 13개는 보이지 않습니다)
1번째 줄: 1번째 줄:
 
==개요==
 
==개요==
−
* 자연수 $r$, $I=\{1\,\cdots, r\}$
+
* <math>r</math> : 자연수  
−
* 변수 $\left(Q^{(a)}_{m}\right)$, $m\in \mathbb{Z}_{\geq 0}$, $a\in I$에 대하여, 다음과 같은 점화식을 생각하자
+
* <math>I=\{1\,\cdots, r\}</math>
 +
* 복소수 <math>T_{m}(u)</math>, <math>u\in \mathbb{Z}_{\geq 0}</math>, <math>m\in I</math>에 대하여, 다음과 같은 점화식을 생각하자
 
\begin{equation}
 
\begin{equation}
 
\label{cf}
 
\label{cf}
 
\left\{
 
\left\{
 
\begin{array}{lll}
 
\begin{array}{lll}
−
Q^{(0)}_{m} =Q^{(r+1)}_{m} =1 & m\in \mathbb{Z}_{\geq 0} \\
+
T_{0}(u) =T_{r+1}(u) =1 & u\in \mathbb{Z}_{\geq 0} \\
−
Q^{(a)}_{m}Q^{(a)}_{m+1}=1+Q^{(a-1)}_{m+1}Q^{(a+1)}_{m} & a\in I, m\in \mathbb{Z}_{\geq 0}
+
T_{m}(u)T_{m}(u+1)=1+T_{m-1}(u+1)T_{m+1}(u) & m\in I, u\in \mathbb{Z}_{\geq 0}
 
\end{array}
 
\end{array}
 
\right.
 
\right.
 
\end{equation}
 
\end{equation}
−
* 아래의 그림은 $r=5$인 경우에 해당하며, $\left(Q^{(a)}_{1}\right)_{a\in I}$가 결정되면, 나머지 $Q^{(a)}_{m}$는 점화식 \ref{cf}로부터 얻어진다
+
* 아래의 그림은 <math>r=5</math>인 경우에 해당하며, <math>\left(T_{m}(1)\right)_{m\in I}</math>가 결정되면, 나머지 <math>T_{m}(u)</math>는 점화식 \ref{cf}로부터 얻어진다
 
[[파일:콕세터 프리즈1.png]]
 
[[파일:콕세터 프리즈1.png]]
  
  
−
* 점화식 \ref{cf}은 다음과 같은 배열이 $ad-bc=1$를 만족시키는 것으로 이해할 수 있다
+
* 점화식 \ref{cf}은 다음과 같은 배열이 <math>ad-bc=1</math>를 만족시키는 것으로 이해할 수 있다
 
[[파일:콕세터 프리즈5.png]]
 
[[파일:콕세터 프리즈5.png]]
 
==예==
 
==예==
 +
===<math>r=2</math>===
 +
* [[5항 관계식 (5-term relation)]]
 +
[[파일:콕세터 프리즈4.png]]
 +
===<math>r=3</math>===
 +
[[파일:콕세터 프리즈6.png]]
 +
 +
[[파일:콕세터 프리즈7.png]]
 +
===<math>r=4</math>===
 
[[파일:콕세터 프리즈2.png]]
 
[[파일:콕세터 프리즈2.png]]
 +
 +
===<math>r=6</math>===
 +
[[파일:콕세터 프리즈3.png]]
 +
 +
 +
  
  
−
[[파일:콕세터 프리즈3.png]]
+
==성질==
 +
===주기성===
 +
* 각 <math>m\in I</math>에 대하여, <math>T_{m}(u+(r+3))=T_{m}(u)</math>이 성립한다
 +
 
 +
===정수 수열===
 +
* 모든 <math>T_{m}(u)</math>, <math>u\in \mathbb{Z}_{\geq 0}</math>, <math>m\in I</math>가 정수가 될 필요충분조건은 다음과 같다
 +
:<math>
 +
T_{m}(1)|\left(T_{m-1}(1)+T_{m+1}(1)\right)
 +
</math>
 +
;(정리) 콕세터-콘웨이
 +
모든 양의 정수로 이루어진 콕세터 프리즈는 정(r+3)-각형의 삼각화로부터 얻어진다
 +
'''[H]''' 정리 4 참조
  
  
−
[[파일:콕세터 프리즈4.png]]
+
==관련된 항목들==
 +
* [[정다각형의 삼각형 분할]]
 +
* [[패리 수열(Farey series)]]
  
  
 
==매스매티카 파일 및 계산 리소스==
 
==매스매티카 파일 및 계산 리소스==
 
* https://docs.google.com/file/d/0B8XXo8Tve1cxbjhtOHUwbTB1S2s/edit?usp=drivesdk
 
* https://docs.google.com/file/d/0B8XXo8Tve1cxbjhtOHUwbTB1S2s/edit?usp=drivesdk
 +
 +
 +
==관련도서==
 +
* Coxeter, H. S. M. 1991. Regular Complex Polytopes. Cambridge [England]; New York: Cambridge University Press. http://www.amazon.com/Regular-Complex-Polytopes-H-Coxeter/dp/0521394902
 +
** Chapter 5
 +
 +
 +
==리뷰, 에세이, 강의노트==
 +
* Morier-Genoud, Sophie. ‘Coxeter’s Frieze Patterns at the Crossroads of Algebra, Geometry and Combinatorics’. arXiv:1503.05049 Null, 17 March 2015. http://arxiv.org/abs/1503.05049.
 +
  
  
 
==관련논문==
 
==관련논문==
 +
* Karin Baur, Klemens Fellner, Mark James Parsons, Manuela Tschabold, Growth behaviour of periodic tame friezes, http://arxiv.org/abs/1603.02127v1
 +
* '''[H]'''Henry, Claire-Soizic. 2013. “Coxeter Friezes and Triangulations of Polygons.” American Mathematical Monthly 120 (6): 553–558. doi:10.4169/amer.math.monthly.120.06.553.
 
* Conway, J. H., and H. S. M. Coxeter. 1973. “Triangulated Polygons and Frieze Patterns.” The Mathematical Gazette 57 (400) (June 1): 87–94. doi:10.2307/3615344.
 
* Conway, J. H., and H. S. M. Coxeter. 1973. “Triangulated Polygons and Frieze Patterns.” The Mathematical Gazette 57 (400) (June 1): 87–94. doi:10.2307/3615344.
 
* Conway, J. H., and H. S. M. Coxeter. 1973. “Triangulated Polygons and Frieze Patterns (Continued).” The Mathematical Gazette 57 (401) (October 1): 175–183. doi:10.2307/3615561.
 
* Conway, J. H., and H. S. M. Coxeter. 1973. “Triangulated Polygons and Frieze Patterns (Continued).” The Mathematical Gazette 57 (401) (October 1): 175–183. doi:10.2307/3615561.
 
* Coxeter, H. S. M. 1971. “Frieze Patterns.” Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica 18: 297–310. https://eudml.org/doc/204992
 
* Coxeter, H. S. M. 1971. “Frieze Patterns.” Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica 18: 297–310. https://eudml.org/doc/204992

2020년 11월 14일 (토) 00:39 기준 최신판

개요

  • \(r\) : 자연수
  • \(I=\{1\,\cdots, r\}\)
  • 복소수 \(T_{m}(u)\), \(u\in \mathbb{Z}_{\geq 0}\), \(m\in I\)에 대하여, 다음과 같은 점화식을 생각하자

\begin{equation} \label{cf} \left\{ \begin{array}{lll} T_{0}(u) =T_{r+1}(u) =1 & u\in \mathbb{Z}_{\geq 0} \\ T_{m}(u)T_{m}(u+1)=1+T_{m-1}(u+1)T_{m+1}(u) & m\in I, u\in \mathbb{Z}_{\geq 0} \end{array} \right. \end{equation}

  • 아래의 그림은 \(r=5\)인 경우에 해당하며, \(\left(T_{m}(1)\right)_{m\in I}\)가 결정되면, 나머지 \(T_{m}(u)\)는 점화식 \ref{cf}로부터 얻어진다

콕세터 프리즈1.png


  • 점화식 \ref{cf}은 다음과 같은 배열이 \(ad-bc=1\)를 만족시키는 것으로 이해할 수 있다

콕세터 프리즈5.png

예

\(r=2\)

콕세터 프리즈4.png

\(r=3\)

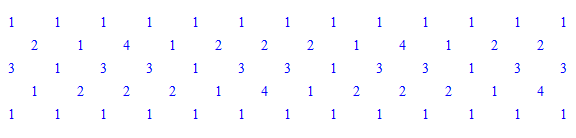
콕세터 프리즈6.png

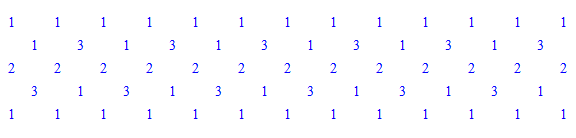
콕세터 프리즈7.png

\(r=4\)

콕세터 프리즈2.png

\(r=6\)

콕세터 프리즈3.png



성질

주기성

  • 각 \(m\in I\)에 대하여, \(T_{m}(u+(r+3))=T_{m}(u)\)이 성립한다

정수 수열

  • 모든 \(T_{m}(u)\), \(u\in \mathbb{Z}_{\geq 0}\), \(m\in I\)가 정수가 될 필요충분조건은 다음과 같다

\[ T_{m}(1)|\left(T_{m-1}(1)+T_{m+1}(1)\right) \]

(정리) 콕세터-콘웨이

모든 양의 정수로 이루어진 콕세터 프리즈는 정(r+3)-각형의 삼각화로부터 얻어진다 [H] 정리 4 참조


관련된 항목들


매스매티카 파일 및 계산 리소스


관련도서


리뷰, 에세이, 강의노트

  • Morier-Genoud, Sophie. ‘Coxeter’s Frieze Patterns at the Crossroads of Algebra, Geometry and Combinatorics’. arXiv:1503.05049 Null, 17 March 2015. http://arxiv.org/abs/1503.05049.


관련논문

  • Karin Baur, Klemens Fellner, Mark James Parsons, Manuela Tschabold, Growth behaviour of periodic tame friezes, http://arxiv.org/abs/1603.02127v1
  • [H]Henry, Claire-Soizic. 2013. “Coxeter Friezes and Triangulations of Polygons.” American Mathematical Monthly 120 (6): 553–558. doi:10.4169/amer.math.monthly.120.06.553.
  • Conway, J. H., and H. S. M. Coxeter. 1973. “Triangulated Polygons and Frieze Patterns.” The Mathematical Gazette 57 (400) (June 1): 87–94. doi:10.2307/3615344.
  • Conway, J. H., and H. S. M. Coxeter. 1973. “Triangulated Polygons and Frieze Patterns (Continued).” The Mathematical Gazette 57 (401) (October 1): 175–183. doi:10.2307/3615561.
  • Coxeter, H. S. M. 1971. “Frieze Patterns.” Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica 18: 297–310. https://eudml.org/doc/204992
원본 주소 "https://wiki.mathnt.net/index.php?title=콕세터_프리즈&oldid=44127"