"Lectures on dilogarithm function"의 두 판 사이의 차이
imported>Pythagoras0 |
Pythagoras0 (토론 | 기여) |
||
| (사용자 2명의 중간 판 17개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==dilogarithm fuction== | ==dilogarithm fuction== | ||
* Define | * Define | ||
| 20번째 줄: | 13번째 줄: | ||
:<math>f(z): = \mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)+\frac{1}{2}\log^2(-z)</math> | :<math>f(z): = \mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)+\frac{1}{2}\log^2(-z)</math> | ||
is constant | is constant | ||
| − | as | + | as <math>f'(z)</math> is |
| − | + | :<math> | |
-\frac{\log (1-z)}{z}+\frac{\log \left(1-\frac{1}{z}\right)}{z}+\frac{\log (-z)}{z}=0 | -\frac{\log (1-z)}{z}+\frac{\log \left(1-\frac{1}{z}\right)}{z}+\frac{\log (-z)}{z}=0 | ||
| − | + | </math> | |
| − | When | + | When <math>z=-1</math>, |
:<math>\mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)+\frac{1}{2}\log^2(-z) = 2\mbox{Li}_ 2(-1)</math> | :<math>\mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)+\frac{1}{2}\log^2(-z) = 2\mbox{Li}_ 2(-1)</math> | ||
| − | When | + | When <math>z=1</math>; |
:<math>2\mbox{Li}_ 2(1)+\frac{1}{2}\log^2(-1) = 2\mbox{Li}_ 2(-1)</math> | :<math>2\mbox{Li}_ 2(1)+\frac{1}{2}\log^2(-1) = 2\mbox{Li}_ 2(-1)</math> | ||
:<math>\frac{\pi^2}{3}-\frac{1}{2}\pi^2 = 2\mbox{Li}_ 2(-1)</math> | :<math>\frac{\pi^2}{3}-\frac{1}{2}\pi^2 = 2\mbox{Li}_ 2(-1)</math> | ||
| 45번째 줄: | 38번째 줄: | ||
;proof | ;proof | ||
Show that | Show that | ||
| − | the partial derivatives of | + | the partial derivatives of <math>F(x,y):=L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)</math> are 0. |
Note | Note | ||
| − | + | :<math> | |
L(h(x))' = -\frac{h'(x) \log (1-h(x))}{2 h(x)}-\frac{h'(x) \log (h(x))}{2 (1-h(x))}. | L(h(x))' = -\frac{h'(x) \log (1-h(x))}{2 h(x)}-\frac{h'(x) \log (h(x))}{2 (1-h(x))}. | ||
| − | + | </math> | |
| − | + | :<math> | |
\begin{aligned} | \begin{aligned} | ||
F_x = & | F_x = & | ||
| − | \frac{1}{2} \left(\frac{\log (x)}{1-x}-\frac{\log (1-x)}{x}\right)+\frac{1}{2} \left(\frac{\log (1-x y)}{x}-\frac{y \log (x y)}{1-x y}\right)+0+\frac{(1-y) | + | \frac{1}{2} \left(\frac{\log (x)}{1-x}-\frac{\log (1-x)}{x}\right)+\frac{1}{2} \left(\frac{\log (1-x y)}{x}-\frac{y \log (x y)}{1-x y}\right)+0 \\ |
| + | & +\frac{(1-y) | ||
\log \left(\frac{1-y}{1-x y}\right)+(1-x) y \log \left(\frac{(1-x) y}{1-x y}\right)}{2 (1-x) (1-x y)}-\frac{(1-x) \log \left(\frac{1-x}{1-x y}\right)+x (1-y) | \log \left(\frac{1-y}{1-x y}\right)+(1-x) y \log \left(\frac{(1-x) y}{1-x y}\right)}{2 (1-x) (1-x y)}-\frac{(1-x) \log \left(\frac{1-x}{1-x y}\right)+x (1-y) | ||
\log \left(\frac{x (1-y)}{1-x y}\right)}{2 (1-x) x (1-x y)} \\ | \log \left(\frac{x (1-y)}{1-x y}\right)}{2 (1-x) x (1-x y)} \\ | ||
& =\frac{1}{2} \log (x)\left(\frac{1}{1-x}+\frac{-y}{1-xy}+\frac{-(1-y)}{(1-x) (1-x y)} \right)+\dots | & =\frac{1}{2} \log (x)\left(\frac{1}{1-x}+\frac{-y}{1-xy}+\frac{-(1-y)}{(1-x) (1-x y)} \right)+\dots | ||
\end{aligned} | \end{aligned} | ||
| − | + | </math> | |
| − | Do the same for | + | Do the same for <math>F_y</math>. |
There is a more systematic way to control the cancellations. | There is a more systematic way to control the cancellations. | ||
| 67번째 줄: | 61번째 줄: | ||
:<math>\frac{d}{dx}L(h(x))=\frac{1}{2}[\log(h(x))\frac{d}{dx}\log (1-h(x))-\log(1-h(x))\frac{d}{dx}\log h(x)]</math> | :<math>\frac{d}{dx}L(h(x))=\frac{1}{2}[\log(h(x))\frac{d}{dx}\log (1-h(x))-\log(1-h(x))\frac{d}{dx}\log h(x)]</math> | ||
| − | For | + | For <math>f,g\in \mathbb{Q}(x,y)</math>, define (symbolically) |
| − | + | :<math> | |
f\wedge g : = \log (f) d (\log (g))-\log (g) d (\log (f)) | f\wedge g : = \log (f) d (\log (g))-\log (g) d (\log (f)) | ||
| − | + | </math> | |
| − | where | + | where <math>df = f_x dx + f_y dy</math>. |
For example, | For example, | ||
| − | + | <math>L'(x)dx =\frac{1}{2} x\wedge (1-x) </math> | |
Then | Then | ||
| 81번째 줄: | 75번째 줄: | ||
So | So | ||
| − | + | :<math> | |
F_x dx+F_y dy = \frac{1}{2}\left(x\wedge (1-x)+(1-x y)\wedge (x y)+y\wedge (1-y)+\frac{1-y}{1-x y}\wedge \left(\frac{y(1-x)}{1-x y}\right)+\frac{1-x}{1-x y}\wedge \left(\frac{x(1-y)}{1-xy}\right) \right)=0 | F_x dx+F_y dy = \frac{1}{2}\left(x\wedge (1-x)+(1-x y)\wedge (x y)+y\wedge (1-y)+\frac{1-y}{1-x y}\wedge \left(\frac{y(1-x)}{1-x y}\right)+\frac{1-x}{1-x y}\wedge \left(\frac{x(1-y)}{1-xy}\right) \right)=0 | ||
| − | + | </math> | |
;remark | ;remark | ||
| 98번째 줄: | 92번째 줄: | ||
;remark | ;remark | ||
Zagier has | Zagier has | ||
| − | + | :<math> | |
\frac{\pi^2}{6}-\log(x)\log(1-x)-\log(y)\log(1-y)+\log (\frac{1-x}{1-xy})\log (\frac{1-y}{1-xy}) | \frac{\pi^2}{6}-\log(x)\log(1-x)-\log(y)\log(1-y)+\log (\frac{1-x}{1-xy})\log (\frac{1-y}{1-xy}) | ||
| − | + | </math> | |
on the RHS, which is not correct | on the RHS, which is not correct | ||
| 122번째 줄: | 116번째 줄: | ||
==Bloch-Wigner dilogarithm== | ==Bloch-Wigner dilogarithm== | ||
| − | * | + | * <math>\operatorname{Li}_2(z)</math> jumps by <math>2\pi i \log|z|</math> as <math>z</math> crosses the cut |
| − | * consider | + | * consider <math>\operatorname{Li}_2(z)+i \log|z|\arg(1-z)</math>, where <math>-\pi <\arg z< \pi</math> |
| − | * when it cross the line | + | * when it cross the line <math>(1,\infty)</math>, it becomes continuous |
;example | ;example | ||
| − | + | :<math> | |
\begin{aligned} | \begin{aligned} | ||
\operatorname{Li}_2(2+0.001i) & = 2.46583 + 2.17759 i \\ | \operatorname{Li}_2(2+0.001i) & = 2.46583 + 2.17759 i \\ | ||
\operatorname{Li}_2(2-0.001i) & = 2.46583 - 2.17759 i | \operatorname{Li}_2(2-0.001i) & = 2.46583 - 2.17759 i | ||
\end{aligned} | \end{aligned} | ||
| − | + | </math> | |
and | and | ||
| − | + | :<math> | |
\begin{aligned} | \begin{aligned} | ||
\log |(2+0.001i)| \arg(1-(2+0.001i)) & = 0. - 2.17689 i \\ | \log |(2+0.001i)| \arg(1-(2+0.001i)) & = 0. - 2.17689 i \\ | ||
\log |(2-0.001i)| \arg(1-(2-0.001i)) & = 0. + 2.17689 i | \log |(2-0.001i)| \arg(1-(2-0.001i)) & = 0. + 2.17689 i | ||
\end{aligned} | \end{aligned} | ||
| − | + | </math> | |
* define | * define | ||
| − | + | :<math>D(z)=\text{Im}(\operatorname{Li}_2(z))+\log|z|\arg(1-z).</math> | |
| − | * real analytic function on | + | * real analytic function on <math>\mathbb{C}</math> except at 0 and 1, where it is continuous but not differentiable. |
| − | * | + | * <math>D(\bar{z})=-D(z)</math>, and vanishes on <math>\mathbb{R}</math>. |
* It satisfies the following functional equations : | * It satisfies the following functional equations : | ||
\begin{equation}\label{functid1} | \begin{equation}\label{functid1} | ||
| 155번째 줄: | 149번째 줄: | ||
==Bloch group== | ==Bloch group== | ||
| − | * Let | + | * Let <math>\mathbb{F}</math> be a field |
* <math>\Lambda^2({\mathbb{F}^{\times}})</math> the set of all formal linear combinations <math>x\wedge y</math>, <math>x,y\in\mathbb{F^{\times}}</math> subject to relations | * <math>\Lambda^2({\mathbb{F}^{\times}})</math> the set of all formal linear combinations <math>x\wedge y</math>, <math>x,y\in\mathbb{F^{\times}}</math> subject to relations | ||
** <math>a\wedge b=-b \wedge a</math> | ** <math>a\wedge b=-b \wedge a</math> | ||
| 167번째 줄: | 161번째 줄: | ||
* The Bloch group is defined to be | * The Bloch group is defined to be | ||
:<math>\mathcal{B}(\mathbb{F})=\mathcal{A}(\mathbb{F})/\mathcal{C}(\mathbb{F})</math> | :<math>\mathcal{B}(\mathbb{F})=\mathcal{A}(\mathbb{F})/\mathcal{C}(\mathbb{F})</math> | ||
| − | * | + | * <math>[x]+[1-x]</math> is in <math>\mathcal{B}(\mathbb{F})</math> |
| − | * Q. is | + | * Q. is <math>[x]+[\frac{1}{x}]</math> in <math>\mathcal{B}(\mathbb{F})</math>? |
;example | ;example | ||
| − | + | <math>F=\mathbb{Q}(\sqrt{-7})</math> | |
| − | + | :<math> | |
2[\frac{1+\sqrt{-7}}{2}]+[\frac{-1+\sqrt{-7}}{4}]\in \mathcal{B}(F) | 2[\frac{1+\sqrt{-7}}{2}]+[\frac{-1+\sqrt{-7}}{4}]\in \mathcal{B}(F) | ||
| − | + | </math> | |
==values of Dedekind zeta at s=2== | ==values of Dedekind zeta at s=2== | ||
===Dedekind zeta=== | ===Dedekind zeta=== | ||
| − | * Let | + | * Let <math>F</math> be a number field with <math>[F:\mathbb{Q}]=r_1+2r_2</math> |
| − | * | + | * <math>\zeta _F(s):= \zeta_F (s) = \sum_{I \subseteq \mathcal{O}_F} \frac{1}{(N_{F/\mathbf{Q}} (I))^{s}}</math> |
* functional equation | * functional equation | ||
:<math>\xi_{F}(s)=\left|d_F\right|{}^{s/2} 2^{r_2 (1-s)} \pi ^{\frac{1}{2} \left(-r_1-2 r_2\right) s}\Gamma \left(\frac{s}{2}\right)^{r_1} \Gamma (s)^{r_2}\zeta _F(s)</math>:<math>\xi_{F}(s) = \xi_{F}(1 - s)</math> | :<math>\xi_{F}(s)=\left|d_F\right|{}^{s/2} 2^{r_2 (1-s)} \pi ^{\frac{1}{2} \left(-r_1-2 r_2\right) s}\Gamma \left(\frac{s}{2}\right)^{r_1} \Gamma (s)^{r_2}\zeta _F(s)</math>:<math>\xi_{F}(s) = \xi_{F}(1 - s)</math> | ||
| − | * at | + | * at <math>s=-n, n=1,2\cdots</math>, <math>\zeta_F(s)</math> has zero of order <math>r_2</math> or <math>r_1+r_2</math> if <math>n</math> is even or odd, respectively |
| − | + | :<math> | |
2^{(m+1) r_2} \pi^{-\frac{1}{2} m \left(-r_1-2 r_2\right)}\zeta_F(-m) \Gamma (-m)^{r_2}\Gamma(-\frac{m}{2} )^{r_1} \left| d_F\right| {}^{-\frac{m}{2}}\\ | 2^{(m+1) r_2} \pi^{-\frac{1}{2} m \left(-r_1-2 r_2\right)}\zeta_F(-m) \Gamma (-m)^{r_2}\Gamma(-\frac{m}{2} )^{r_1} \left| d_F\right| {}^{-\frac{m}{2}}\\ | ||
=2^{-m r_2} \pi ^{\frac{1}{2} (m+1) \left(-r_1-2 r_2\right)} \zeta _F(m+1)\Gamma(\frac{m+1}{2})^{r_1}\Gamma (m+1)^{r_2} \left| d_F\right| {}^{\frac{m+1}{2}} | =2^{-m r_2} \pi ^{\frac{1}{2} (m+1) \left(-r_1-2 r_2\right)} \zeta _F(m+1)\Gamma(\frac{m+1}{2})^{r_1}\Gamma (m+1)^{r_2} \left| d_F\right| {}^{\frac{m+1}{2}} | ||
| − | + | </math> | |
===Dirichlet class number formula=== | ===Dirichlet class number formula=== | ||
* residue at <math>s=1</math> | * residue at <math>s=1</math> | ||
:<math> \lim_{s\to 1} (s-1)\zeta_F(s)=\frac{2^{r_1}\cdot(2\pi)^{r_2}\cdot h_F\cdot R_F}{w_F \cdot \sqrt{|d_F|}}</math> | :<math> \lim_{s\to 1} (s-1)\zeta_F(s)=\frac{2^{r_1}\cdot(2\pi)^{r_2}\cdot h_F\cdot R_F}{w_F \cdot \sqrt{|d_F|}}</math> | ||
| − | * equivalently, | + | * equivalently, <math>\zeta _F(s)</math> has zero of order <math>r_1+r_2-1</math> at <math>s=0</math> |
:<math> \lim_{s\to 0}\frac{\zeta_F(s)}{s^{r_1+r_2-1}}=-\frac{h_F R_F}{w_F}</math> | :<math> \lim_{s\to 0}\frac{\zeta_F(s)}{s^{r_1+r_2-1}}=-\frac{h_F R_F}{w_F}</math> | ||
===algebraic K-theory=== | ===algebraic K-theory=== | ||
| − | * | + | * <math>F</math> : number field |
| − | * | + | * <math>K_0(F) = \mathbb{Z}</math> |
| − | * | + | * <math>K_1(F) = F^{\times}</math> |
| − | * | + | * <math>K_2(F) = F^{\times}\otimes F^{\times}/\langle x\otimes (1-x) \rangle</math> |
| − | * | + | * <math>K_0(\mathcal{O}_F) = \mathbb{Z}\oplus Cl_F</math> |
| − | * | + | * <math>K_1(\mathcal{O}_F) = (\mathcal{O}_F)^{\times}</math> |
| − | * | + | * <math>K_2(\mathcal{O}_F)</math> : finite group |
===Borel's regulator=== | ===Borel's regulator=== | ||
* Borel constructed a map | * Borel constructed a map | ||
| − | + | :<math> | |
K_{2i-1}(F) \to \mathbb{R}^{d_{i}},\, i\geq 2 | K_{2i-1}(F) \to \mathbb{R}^{d_{i}},\, i\geq 2 | ||
| − | + | </math> | |
| − | where | + | where <math>d_i = r_2</math>, or <math>r_1+r_2</math> depending on the parity of <math>i</math> |
* this can be used to show | * this can be used to show | ||
| − | ** | + | ** <math>\operatorname{rank} K_3 =d_2 = r_2</math> |
| − | ** | + | ** <math>\operatorname{rank} K_5=d_3 = r_1+r_2</math> |
| − | ** | + | ** <math>\operatorname{rank} K_7=d_4 = r_2</math> |
| − | * the covolume of the image under this regulator is a non-zero multiple of | + | * the covolume of the image of <math>K_m,\, m=2i-1</math> under this regulator is a non-zero multiple of |
| − | + | :<math>\frac{|d_{F}|^{1/2}}{\pi^{md_{i+1}}} \zeta_{F}(m)</math> | |
| + | * for <math>K_3</math>, <math>\frac{|d_{F}|^{1/2}}{\pi^{m(r_1+r_2)}} \zeta_{F}(2)</math> | ||
* this is a generalization of Dirichlet's class number formula | * this is a generalization of Dirichlet's class number formula | ||
| − | * the rational number given by the ratio is related to other | + | * the rational number given by the ratio is related to other <math>K</math>-groups (Lichtenbaum conjecture) |
===Zagier, Bloch, Suslin=== | ===Zagier, Bloch, Suslin=== | ||
| − | * The Bloch-Wigner dilogarithm | + | * The Bloch-Wigner dilogarithm <math>D(z)</math> can be used to define a map from <math>\mathcal{B}(\mathbb{C})</math> to <math>\mathbb{R}</math>. |
| − | * For | + | * For <math>\xi=\sum_{i} n_i[x_i] \in \mathcal{B}(\mathbb{C})</math>, let <math>D(\xi)=\sum_{i} n_i D(x_i)</math>. |
| − | * by the 5-term relation satisfied by | + | * by the 5-term relation satisfied by <math>D</math>, it is well-defined |
| − | * For an embedding | + | * For an embedding <math>\sigma : F\hookrightarrow \mathbb{C}</math> and <math>\xi \in \mathcal{B}(F)</math>, we may consider <math>D\left(\sigma(\xi)\right)</math>. |
| − | * If | + | * If <math>D\left(\sigma(\xi)\right)=0</math> for all such embeddings <math>\sigma</math>, then <math>\xi \in \mathcal{B}(F)</math> is a torsion element in <math>\mathcal{B}(F)</math>. |
| − | * | + | * Bloch and Suslin connects <math>K_3</math> with the Bloch group |
| + | * <math>D</math> is compatible with Borel's regulator | ||
:<math> | :<math> | ||
\frac{|d_{F}|^{1/2}}{\pi^{2(r_1 + r_2)}} \zeta_{F}(2) | \frac{|d_{F}|^{1/2}}{\pi^{2(r_1 + r_2)}} \zeta_{F}(2) | ||
\sim_{\mathbb{Q^{\times}}} \det\left(D(\sigma_i(\xi_j))\right)_{1\leq i,j\leq r_2} | \sim_{\mathbb{Q^{\times}}} \det\left(D(\sigma_i(\xi_j))\right)_{1\leq i,j\leq r_2} | ||
</math> | </math> | ||
| − | where <math>\xi_i,(i=1,\cdots, r_2)</math> is | + | where <math>\xi_i,(i=1,\cdots, r_2)</math> is <math>\mathbb{Q}</math>-basis of <math>\mathcal{B}(F)\otimes \mathbb{Q}</math> and <math>a\sim_{\mathbb{Q^{\times}}} b</math> means <math>a/b\in\mathbb{Q}</math> |
;example | ;example | ||
| − | + | <math>F=\mathbb{Q}(\sqrt{-7})</math> | |
| − | + | :<math> | |
\zeta_F(2) = \frac{4 \pi ^2}{21 \sqrt{7}} \left(D\left(\frac{-1+\sqrt{-7}}{4} \right)+2 D\left(\frac{1+ \sqrt{-7}}{2} \right)\right) =1.8948414489688\dots | \zeta_F(2) = \frac{4 \pi ^2}{21 \sqrt{7}} \left(D\left(\frac{-1+\sqrt{-7}}{4} \right)+2 D\left(\frac{1+ \sqrt{-7}}{2} \right)\right) =1.8948414489688\dots | ||
| − | + | </math> | |
| − | + | <math>F=\mathbb{Q}(\sqrt{-23})</math> | |
| − | + | :<math> | |
| − | \zeta_F(2) = \frac{4 \pi ^2}{69 \sqrt{23}}\left(21D\left(\frac{1}{2} \left(1+\sqrt{-23}\right)\right)+7D\left(2+\sqrt{-23}\right)+D\left(\frac{1}{2} \left(3+\sqrt{-23}\right)\right)+D\left(3+\sqrt{-23}\right)-3D\left(\frac{1}{2} \left(5+\sqrt{-23}\right)\right)\right) = 2.3081992895457\dots | + | \begin{aligned} |
| − | + | \zeta_F(2) & = \frac{4 \pi ^2}{69 \sqrt{23}}\left(21D\left(\frac{1}{2} \left(1+\sqrt{-23}\right)\right)+7D\left(2+\sqrt{-23}\right)+D\left(\frac{1}{2} \left(3+\sqrt{-23}\right)\right)+D\left(3+\sqrt{-23}\right)-3D\left(\frac{1}{2} \left(5+\sqrt{-23}\right)\right)\right) \\ | |
| + | & = 2.3081992895457\dots | ||
| + | \end{aligned} | ||
| + | </math> | ||
==hyperbolic 3-manifold== | ==hyperbolic 3-manifold== | ||
| − | * | + | * <math>\mathbb{H}^3</math> : upper-half space; <math>SL_2(\mathbb{C})</math> acts as an isometry group |
| − | * hyperbolic 3-manifold : quotient of | + | * hyperbolic 3-manifold : quotient of <math>\mathbb{H}^3</math> by discrete isometry group |
| − | * ideal tetrahedron is a tetrahedron whose vertices are in | + | * ideal tetrahedron is a tetrahedron whose vertices are in <math>\mathbb{C}\cup \{\infty\}</math> |
| − | * let | + | * let <math>\tilde{D}(z_0,z_1,z_2,z_3) : = D\left(\frac{\left(z_0-z_2\right) \left(z_1-z_3\right)}{\left(z_1-z_2\right) \left(z_0-z_3\right)}\right)</math> |
;fact | ;fact | ||
| − | Let | + | Let <math>\Delta</math> an ideal tetrahedron with vertices <math>z_0,z_1,z_2,z_3</math>. Then its volume is given by <math>\tilde{D}(z_0,z_1,z_2,z_3)</math>. |
;fact | ;fact | ||
| − | # A complete oriented hyperbolic 3-manifold with finite volume can be triangulated into ideal tetrahedra | + | # A complete oriented hyperbolic 3-manifold with finite volume can be triangulated into ideal tetrahedra <math>\Delta_1,\dots, \Delta_{\nu}</math>. |
| − | # If we assume that the vertices of each tetrahedon are at | + | # If we assume that the vertices of each tetrahedon are at <math>\infty, 0,1</math> and <math>z_{i}</math>, then |
| − | + | :<math> | |
[z_1]+\dots + [z_{\nu}]\in \mathcal{B}_{\mathbb{C}} | [z_1]+\dots + [z_{\nu}]\in \mathcal{B}_{\mathbb{C}} | ||
| − | + | </math> | |
| − | and the volume is given by | + | and the volume is given by <math>\sum D(z_i)</math>. |
===five-term relation reinterpreted=== | ===five-term relation reinterpreted=== | ||
* Pachner move : sum of two tetrahedra = sum of three tetrahedra | * Pachner move : sum of two tetrahedra = sum of three tetrahedra | ||
* it implies | * it implies | ||
| − | + | :<math> | |
D\left(\frac{\left(z_0-z_2\right) \left(z_1-z_3\right)}{\left(z_1-z_2\right) \left(z_0-z_3\right)}\right)-D\left(\frac{\left(z_0-z_2\right) | D\left(\frac{\left(z_0-z_2\right) \left(z_1-z_3\right)}{\left(z_1-z_2\right) \left(z_0-z_3\right)}\right)-D\left(\frac{\left(z_0-z_2\right) | ||
\left(z_1-z_4\right)}{\left(z_1-z_2\right) \left(z_0-z_4\right)}\right)+D\left(\frac{\left(z_0-z_3\right) \left(z_1-z_4\right)}{\left(z_1-z_3\right) | \left(z_1-z_4\right)}{\left(z_1-z_2\right) \left(z_0-z_4\right)}\right)+D\left(\frac{\left(z_0-z_3\right) \left(z_1-z_4\right)}{\left(z_1-z_3\right) | ||
\left(z_0-z_4\right)}\right)-D\left(\frac{\left(z_0-z_3\right) \left(z_2-z_4\right)}{\left(z_2-z_3\right) | \left(z_0-z_4\right)}\right)-D\left(\frac{\left(z_0-z_3\right) \left(z_2-z_4\right)}{\left(z_2-z_3\right) | ||
\left(z_0-z_4\right)}\right)+D\left(\frac{\left(z_1-z_3\right) \left(z_2-z_4\right)}{\left(z_2-z_3\right) \left(z_1-z_4\right)}\right)=0 | \left(z_0-z_4\right)}\right)+D\left(\frac{\left(z_1-z_3\right) \left(z_2-z_4\right)}{\left(z_2-z_3\right) \left(z_1-z_4\right)}\right)=0 | ||
| − | + | </math> | |
| − | * if we set | + | * if we set <math>z_0=\infty,z_1= 0,z_2= 1,z_3= x,z_4 = x y</math>, we get |
| − | + | :<math> | |
D(x)-D(x y)+D(y)+D\left(\frac{1-x y}{y(1-x)}\right)-D\left(\frac{1-x y}{1-x}\right) = 0 | D(x)-D(x y)+D(y)+D\left(\frac{1-x y}{y(1-x)}\right)-D\left(\frac{1-x y}{1-x}\right) = 0 | ||
| − | + | </math> | |
;example (volume of regular ideal tetrahedron) | ;example (volume of regular ideal tetrahedron) | ||
| − | * | + | * <math>\Delta_4</math> : ideal tetrahedron with vertices <math>\infty,0,1,e^{2\pi i/3}</math> |
| − | * volume form on | + | * volume form on <math>\mathbb{H}^3</math> : <math>\frac{dx\,dy\,dz}{z^3}</math>. So the volume of <math>\Delta_4</math> is |
| − | + | :<math> | |
\begin{aligned} | \begin{aligned} | ||
\int\int\int_{\Delta_4}\frac{dx\,dy\,dz}{z^3} & = \int\int_{\Delta_3}\int_{h(x,y)}^{\infty}\frac{1}{z^3}\,dz\,dx\,dy \\ | \int\int\int_{\Delta_4}\frac{dx\,dy\,dz}{z^3} & = \int\int_{\Delta_3}\int_{h(x,y)}^{\infty}\frac{1}{z^3}\,dz\,dx\,dy \\ | ||
& = \int\int_{\Delta_3}\frac{1}{2h(x,y)^2}\,dx\,dy \\ | & = \int\int_{\Delta_3}\frac{1}{2h(x,y)^2}\,dx\,dy \\ | ||
\end{aligned} | \end{aligned} | ||
| − | + | </math> | |
* this integral becomes | * this integral becomes | ||
| − | + | :<math> | |
\int\int_{\Delta_3'}\frac{1}{2(\frac{1}{3}-x^2-y^2)}\,dx\,dy = 1.01494\dots | \int\int_{\Delta_3'}\frac{1}{2(\frac{1}{3}-x^2-y^2)}\,dx\,dy = 1.01494\dots | ||
| − | + | </math> | |
| − | where | + | where <math>\Delta_3'</math> is the triangle with vertices <math>0,1,e^{2\pi i/3}</math> translated so that they lie on the circle with center <math>(0,0)</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==메모== | ||
===Bloch-Suslin=== | ===Bloch-Suslin=== | ||
* <math>B(\mathbb{F})\simeq K_3^{\operatorname{ind}}(\mathbb{F})</math> ?? | * <math>B(\mathbb{F})\simeq K_3^{\operatorname{ind}}(\mathbb{F})</math> ?? | ||
* <math>0\to \tilde{\mu_{F}}\to K_3^{\operatorname{ind}}(\mathbb{F}) \to B(\mathbb{F})\to 0</math> where <math>0\to \mathbb{Z}/\mathbb{Z}_2 \to \tilde{\mu_{F}} \to \mu_{F}\to 0</math> where \mu_{F} is the unit group of F | * <math>0\to \tilde{\mu_{F}}\to K_3^{\operatorname{ind}}(\mathbb{F}) \to B(\mathbb{F})\to 0</math> where <math>0\to \mathbb{Z}/\mathbb{Z}_2 \to \tilde{\mu_{F}} \to \mu_{F}\to 0</math> where \mu_{F} is the unit group of F | ||
| − | * | + | * <math>K_3^{\operatorname{ind}}(\mathbb{F})</math> is a quotient of Milnor K3 by something else |
| − | * functional equation of | + | * functional equation of <math>\zeta_K</math> implies |
| − | + | :<math> | |
\pi^{-d_m} \lim_{s\to -m}\frac{\zeta_K(-m)}{(s+m)^{d_m}} \sim_{\mathbb{Q}^{\times}}\pi ^{-(m+1)(r_1+2 r_2)} \zeta _K(m+1)\left| d_K\right| {}^{\frac{1}{2}} | \pi^{-d_m} \lim_{s\to -m}\frac{\zeta_K(-m)}{(s+m)^{d_m}} \sim_{\mathbb{Q}^{\times}}\pi ^{-(m+1)(r_1+2 r_2)} \zeta _K(m+1)\left| d_K\right| {}^{\frac{1}{2}} | ||
| − | + | </math> | |
| − | where | + | where <math>d_1 =d_3=\dots = r_2</math> or <math>d_2=d_4=\dots =r_1+r_2</math> |
==related items== | ==related items== | ||
| 314번째 줄: | 305번째 줄: | ||
* [[Bloch group]] | * [[Bloch group]] | ||
* [[Ideal triangulations of 3-manifolds and the Bloch invariant]] | * [[Ideal triangulations of 3-manifolds and the Bloch invariant]] | ||
| + | * [[Talk on dilogarithm function and five-term relation]] | ||
| + | |||
==links== | ==links== | ||
| 320번째 줄: | 313번째 줄: | ||
* {{수학노트|url=블로흐-비그너_다이로그(Bloch-Wigner_dilogarithm)}} | * {{수학노트|url=블로흐-비그너_다이로그(Bloch-Wigner_dilogarithm)}} | ||
* {{수학노트|url=함수_다이로그_항등식(functional_dilogarithm_identity)}} | * {{수학노트|url=함수_다이로그_항등식(functional_dilogarithm_identity)}} | ||
| + | |||
| + | [[분류:Talks and lecture notes]] | ||
| + | [[분류:migrate]] | ||
2020년 12월 28일 (월) 04:07 기준 최신판
dilogarithm fuction
- Define
\[\operatorname{Li}_ 2(z)= \sum_{n=1}^\infty {z^n \over n^2},\, |z|<1\]
- extend domain
\[\operatorname{Li}_ 2(z) = -\int_0^z{{\log (1-t)}\over t} dt,\, z\in \mathbb C\backslash [1,\infty) \]
functional equations
- reflection properties
\[\mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)= -\frac{\pi^2}{6}-\frac{1}{2}\log^2(-z)\] \[\mbox{Li}_ 2(z)+\mbox{Li}_ 2(1-z)= \frac{\pi^2}{6}-\log(z)\log(1-z)\]
- proof
\[f(z): = \mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)+\frac{1}{2}\log^2(-z)\] is constant as \(f'(z)\) is \[ -\frac{\log (1-z)}{z}+\frac{\log \left(1-\frac{1}{z}\right)}{z}+\frac{\log (-z)}{z}=0 \]
When \(z=-1\),
\[\mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)+\frac{1}{2}\log^2(-z) = 2\mbox{Li}_ 2(-1)\]
When \(z=1\); \[2\mbox{Li}_ 2(1)+\frac{1}{2}\log^2(-1) = 2\mbox{Li}_ 2(-1)\] \[\frac{\pi^2}{3}-\frac{1}{2}\pi^2 = 2\mbox{Li}_ 2(-1)\]
■
- five-term relation
\[\mbox{Li}_ 2(x)+\mbox{Li}_ 2(y)+\mbox{Li}_ 2 \left( \frac{1-x}{1-xy} \right)+\mbox{Li}_ 2(1-xy)+\mbox{Li}_ 2 \left( \frac{1-y}{1-xy} \right)=\text{something elementary}\]
Let us state this in terms of the Rogers dilogarithm (no worry about the branches) \[L(x): =\operatorname{Li}_ 2(x)+\frac{1}{2}\log x\log (1-x)=-\frac{1}{2}\int_{0}^{x}\left(\frac{\log(1-y)}{y}+\frac{\log(y)}{1-y}\right)dy,\, x\in (0,1)\]
- \(0\leq x,y\leq 1\)
\[L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)=\frac{\pi^2}{2}\]
- proof
Show that the partial derivatives of \(F(x,y):=L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)\) are 0. Note \[ L(h(x))' = -\frac{h'(x) \log (1-h(x))}{2 h(x)}-\frac{h'(x) \log (h(x))}{2 (1-h(x))}. \]
\[ \begin{aligned} F_x = & \frac{1}{2} \left(\frac{\log (x)}{1-x}-\frac{\log (1-x)}{x}\right)+\frac{1}{2} \left(\frac{\log (1-x y)}{x}-\frac{y \log (x y)}{1-x y}\right)+0 \\ & +\frac{(1-y) \log \left(\frac{1-y}{1-x y}\right)+(1-x) y \log \left(\frac{(1-x) y}{1-x y}\right)}{2 (1-x) (1-x y)}-\frac{(1-x) \log \left(\frac{1-x}{1-x y}\right)+x (1-y) \log \left(\frac{x (1-y)}{1-x y}\right)}{2 (1-x) x (1-x y)} \\ & =\frac{1}{2} \log (x)\left(\frac{1}{1-x}+\frac{-y}{1-xy}+\frac{-(1-y)}{(1-x) (1-x y)} \right)+\dots \end{aligned} \] Do the same for \(F_y\).
There is a more systematic way to control the cancellations.
Observe \[\frac{d}{dx}L(h(x))=\frac{1}{2}[\log(h(x))\frac{d}{dx}\log (1-h(x))-\log(1-h(x))\frac{d}{dx}\log h(x)]\]
For \(f,g\in \mathbb{Q}(x,y)\), define (symbolically) \[ f\wedge g : = \log (f) d (\log (g))-\log (g) d (\log (f)) \] where \(df = f_x dx + f_y dy\).
For example, \(L'(x)dx =\frac{1}{2} x\wedge (1-x) \)
Then
- \(f\wedge g=-f \wedge g\)
- \((f_1f_2)\wedge g=f_1\wedge g+f_2\wedge g\)
So \[ F_x dx+F_y dy = \frac{1}{2}\left(x\wedge (1-x)+(1-x y)\wedge (x y)+y\wedge (1-y)+\frac{1-y}{1-x y}\wedge \left(\frac{y(1-x)}{1-x y}\right)+\frac{1-x}{1-x y}\wedge \left(\frac{x(1-y)}{1-xy}\right) \right)=0 \]
- remark
- recurrence relation
\[1-x_{i}=x_{i-1}x_{i+1},\, x_0=x,\, x_2=y\]
- 5-periodic solution
\[x_0=x, x_1=1-xy, x_2=y, x_3=\frac{1-y}{1-xy}, x_4=\frac{1-x}{1-xy}\]
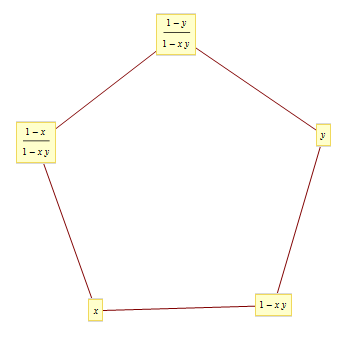
- remark
- we believe(?) all functional equations are coming from the five-term relation
- remark
Zagier has \[ \frac{\pi^2}{6}-\log(x)\log(1-x)-\log(y)\log(1-y)+\log (\frac{1-x}{1-xy})\log (\frac{1-y}{1-xy}) \] on the RHS, which is not correct
special values
\(\mbox{Li}_{2}(0)=0\)
\(\mbox{Li}_{2}(1)=\frac{\pi^2}{6}\)
\(\mbox{Li}_{2}(-1)=-\frac{\pi^2}{12}\)
\(\mbox{Li}_{2}(\frac{1}{2})=\frac{\pi^2}{12}-\frac{1}{2}\log^2(2)\)
\(\mbox{Li}_{2}(\frac{3-\sqrt{5}}{2})=\frac{\pi^2}{15}-\log^2(\frac{1+\sqrt{5}}{2})\)
\(\mbox{Li}_{2}(\frac{-1+\sqrt{5}}{2})=\frac{\pi^2}{10}-\log^2(\frac{1+\sqrt{5}}{2})\)
\(\mbox{Li}_{2}(\frac{1-\sqrt{5}}{2})=-\frac{\pi^2}{15}+\frac{1}{2}\log^2(\frac{1+\sqrt{5}}{2})\)
\(\mbox{Li}_{2}(\frac{-1-\sqrt{5}}{2})=-\frac{\pi^2}{10}+\frac{1}{2}\log^2(\frac{1+\sqrt{5}}{2})\)
Bloch-Wigner dilogarithm
- \(\operatorname{Li}_2(z)\) jumps by \(2\pi i \log|z|\) as \(z\) crosses the cut
- consider \(\operatorname{Li}_2(z)+i \log|z|\arg(1-z)\), where \(-\pi <\arg z< \pi\)
- when it cross the line \((1,\infty)\), it becomes continuous
- example
\[ \begin{aligned} \operatorname{Li}_2(2+0.001i) & = 2.46583 + 2.17759 i \\ \operatorname{Li}_2(2-0.001i) & = 2.46583 - 2.17759 i \end{aligned} \] and \[ \begin{aligned} \log |(2+0.001i)| \arg(1-(2+0.001i)) & = 0. - 2.17689 i \\ \log |(2-0.001i)| \arg(1-(2-0.001i)) & = 0. + 2.17689 i \end{aligned} \]
- define
\[D(z)=\text{Im}(\operatorname{Li}_2(z))+\log|z|\arg(1-z).\]
- real analytic function on \(\mathbb{C}\) except at 0 and 1, where it is continuous but not differentiable.
- \(D(\bar{z})=-D(z)\), and vanishes on \(\mathbb{R}\).
- It satisfies the following functional equations :
\begin{equation}\label{functid1} D(x)+D(1-xy)+D(y)+D(\frac{1-y}{1-xy})+D(\frac{1-x}{1-xy})=0, \end{equation} \begin{equation}\label{functid2} D(x)+D(1-x) =D(x)+D(\frac{1}{x})=0. \end{equation}
Bloch group
- Let \(\mathbb{F}\) be a field
- \(\Lambda^2({\mathbb{F}^{\times}})\) the set of all formal linear combinations \(x\wedge y\), \(x,y\in\mathbb{F^{\times}}\) subject to relations
- \(a\wedge b=-b \wedge a\)
- \((x_1x_2)\wedge y=x_1\wedge y+x_2\wedge y\)
- \(\mathbb{Z}[\mathbb{F}^{\times}\backslash\{1\}]\)
- i.e. abelian group of formal sums \([x_1]+[x_2]+\cdots+[x_n]\), \(x_1,x_2,\cdots,x_n\in \mathbb{F}\backslash\{0,1\}\)
- \(\partial : \mathbb{Z}[\mathbb{F}^{\times}\backslash\{1\}] \to \Lambda^2({\mathbb{F}^{\times}})\)
- \([x]\to x\wedge (1-x)\)
- Let \(\mathcal{A}(\mathbb{F})=\operatorname{ker}\partial\) and \(\mathcal{C}(\mathbb{F})\) subgroup of \(\mathcal{A}(\mathbb{F})=\operatorname{ker}\partial\) generated by
\[[x]+[1-xy]+[y]+[\frac{1-y}{1-xy}]+[\frac{1-x}{1-xy}]\]
- The Bloch group is defined to be
\[\mathcal{B}(\mathbb{F})=\mathcal{A}(\mathbb{F})/\mathcal{C}(\mathbb{F})\]
- \([x]+[1-x]\) is in \(\mathcal{B}(\mathbb{F})\)
- Q. is \([x]+[\frac{1}{x}]\) in \(\mathcal{B}(\mathbb{F})\)?
- example
\(F=\mathbb{Q}(\sqrt{-7})\)
\[ 2[\frac{1+\sqrt{-7}}{2}]+[\frac{-1+\sqrt{-7}}{4}]\in \mathcal{B}(F) \]
values of Dedekind zeta at s=2
Dedekind zeta
- Let \(F\) be a number field with \([F:\mathbb{Q}]=r_1+2r_2\)
- \(\zeta _F(s):= \zeta_F (s) = \sum_{I \subseteq \mathcal{O}_F} \frac{1}{(N_{F/\mathbf{Q}} (I))^{s}}\)
- functional equation
\[\xi_{F}(s)=\left|d_F\right|{}^{s/2} 2^{r_2 (1-s)} \pi ^{\frac{1}{2} \left(-r_1-2 r_2\right) s}\Gamma \left(\frac{s}{2}\right)^{r_1} \Gamma (s)^{r_2}\zeta _F(s)\]\[\xi_{F}(s) = \xi_{F}(1 - s)\]
- at \(s=-n, n=1,2\cdots\), \(\zeta_F(s)\) has zero of order \(r_2\) or \(r_1+r_2\) if \(n\) is even or odd, respectively
\[ 2^{(m+1) r_2} \pi^{-\frac{1}{2} m \left(-r_1-2 r_2\right)}\zeta_F(-m) \Gamma (-m)^{r_2}\Gamma(-\frac{m}{2} )^{r_1} \left| d_F\right| {}^{-\frac{m}{2}}\\ =2^{-m r_2} \pi ^{\frac{1}{2} (m+1) \left(-r_1-2 r_2\right)} \zeta _F(m+1)\Gamma(\frac{m+1}{2})^{r_1}\Gamma (m+1)^{r_2} \left| d_F\right| {}^{\frac{m+1}{2}} \]
Dirichlet class number formula
- residue at \(s=1\)
\[ \lim_{s\to 1} (s-1)\zeta_F(s)=\frac{2^{r_1}\cdot(2\pi)^{r_2}\cdot h_F\cdot R_F}{w_F \cdot \sqrt{|d_F|}}\]
- equivalently, \(\zeta _F(s)\) has zero of order \(r_1+r_2-1\) at \(s=0\)
\[ \lim_{s\to 0}\frac{\zeta_F(s)}{s^{r_1+r_2-1}}=-\frac{h_F R_F}{w_F}\]
algebraic K-theory
- \(F\) : number field
- \(K_0(F) = \mathbb{Z}\)
- \(K_1(F) = F^{\times}\)
- \(K_2(F) = F^{\times}\otimes F^{\times}/\langle x\otimes (1-x) \rangle\)
- \(K_0(\mathcal{O}_F) = \mathbb{Z}\oplus Cl_F\)
- \(K_1(\mathcal{O}_F) = (\mathcal{O}_F)^{\times}\)
- \(K_2(\mathcal{O}_F)\) : finite group
Borel's regulator
- Borel constructed a map
\[ K_{2i-1}(F) \to \mathbb{R}^{d_{i}},\, i\geq 2 \] where \(d_i = r_2\), or \(r_1+r_2\) depending on the parity of \(i\)
- this can be used to show
- \(\operatorname{rank} K_3 =d_2 = r_2\)
- \(\operatorname{rank} K_5=d_3 = r_1+r_2\)
- \(\operatorname{rank} K_7=d_4 = r_2\)
- the covolume of the image of \(K_m,\, m=2i-1\) under this regulator is a non-zero multiple of
\[\frac{|d_{F}|^{1/2}}{\pi^{md_{i+1}}} \zeta_{F}(m)\]
- for \(K_3\), \(\frac{|d_{F}|^{1/2}}{\pi^{m(r_1+r_2)}} \zeta_{F}(2)\)
- this is a generalization of Dirichlet's class number formula
- the rational number given by the ratio is related to other \(K\)-groups (Lichtenbaum conjecture)
Zagier, Bloch, Suslin
- The Bloch-Wigner dilogarithm \(D(z)\) can be used to define a map from \(\mathcal{B}(\mathbb{C})\) to \(\mathbb{R}\).
- For \(\xi=\sum_{i} n_i[x_i] \in \mathcal{B}(\mathbb{C})\), let \(D(\xi)=\sum_{i} n_i D(x_i)\).
- by the 5-term relation satisfied by \(D\), it is well-defined
- For an embedding \(\sigma : F\hookrightarrow \mathbb{C}\) and \(\xi \in \mathcal{B}(F)\), we may consider \(D\left(\sigma(\xi)\right)\).
- If \(D\left(\sigma(\xi)\right)=0\) for all such embeddings \(\sigma\), then \(\xi \in \mathcal{B}(F)\) is a torsion element in \(\mathcal{B}(F)\).
- Bloch and Suslin connects \(K_3\) with the Bloch group
- \(D\) is compatible with Borel's regulator
\[ \frac{|d_{F}|^{1/2}}{\pi^{2(r_1 + r_2)}} \zeta_{F}(2) \sim_{\mathbb{Q^{\times}}} \det\left(D(\sigma_i(\xi_j))\right)_{1\leq i,j\leq r_2} \] where \(\xi_i,(i=1,\cdots, r_2)\) is \(\mathbb{Q}\)-basis of \(\mathcal{B}(F)\otimes \mathbb{Q}\) and \(a\sim_{\mathbb{Q^{\times}}} b\) means \(a/b\in\mathbb{Q}\)
- example
\(F=\mathbb{Q}(\sqrt{-7})\)
\[ \zeta_F(2) = \frac{4 \pi ^2}{21 \sqrt{7}} \left(D\left(\frac{-1+\sqrt{-7}}{4} \right)+2 D\left(\frac{1+ \sqrt{-7}}{2} \right)\right) =1.8948414489688\dots \]
\(F=\mathbb{Q}(\sqrt{-23})\)
\[ \begin{aligned} \zeta_F(2) & = \frac{4 \pi ^2}{69 \sqrt{23}}\left(21D\left(\frac{1}{2} \left(1+\sqrt{-23}\right)\right)+7D\left(2+\sqrt{-23}\right)+D\left(\frac{1}{2} \left(3+\sqrt{-23}\right)\right)+D\left(3+\sqrt{-23}\right)-3D\left(\frac{1}{2} \left(5+\sqrt{-23}\right)\right)\right) \\ & = 2.3081992895457\dots \end{aligned} \]
hyperbolic 3-manifold
- \(\mathbb{H}^3\) : upper-half space; \(SL_2(\mathbb{C})\) acts as an isometry group
- hyperbolic 3-manifold : quotient of \(\mathbb{H}^3\) by discrete isometry group
- ideal tetrahedron is a tetrahedron whose vertices are in \(\mathbb{C}\cup \{\infty\}\)
- let \(\tilde{D}(z_0,z_1,z_2,z_3) : = D\left(\frac{\left(z_0-z_2\right) \left(z_1-z_3\right)}{\left(z_1-z_2\right) \left(z_0-z_3\right)}\right)\)
- fact
Let \(\Delta\) an ideal tetrahedron with vertices \(z_0,z_1,z_2,z_3\). Then its volume is given by \(\tilde{D}(z_0,z_1,z_2,z_3)\).
- fact
- A complete oriented hyperbolic 3-manifold with finite volume can be triangulated into ideal tetrahedra \(\Delta_1,\dots, \Delta_{\nu}\).
- If we assume that the vertices of each tetrahedon are at \(\infty, 0,1\) and \(z_{i}\), then
\[ [z_1]+\dots + [z_{\nu}]\in \mathcal{B}_{\mathbb{C}} \] and the volume is given by \(\sum D(z_i)\).
five-term relation reinterpreted
- Pachner move : sum of two tetrahedra = sum of three tetrahedra
- it implies
\[ D\left(\frac{\left(z_0-z_2\right) \left(z_1-z_3\right)}{\left(z_1-z_2\right) \left(z_0-z_3\right)}\right)-D\left(\frac{\left(z_0-z_2\right) \left(z_1-z_4\right)}{\left(z_1-z_2\right) \left(z_0-z_4\right)}\right)+D\left(\frac{\left(z_0-z_3\right) \left(z_1-z_4\right)}{\left(z_1-z_3\right) \left(z_0-z_4\right)}\right)-D\left(\frac{\left(z_0-z_3\right) \left(z_2-z_4\right)}{\left(z_2-z_3\right) \left(z_0-z_4\right)}\right)+D\left(\frac{\left(z_1-z_3\right) \left(z_2-z_4\right)}{\left(z_2-z_3\right) \left(z_1-z_4\right)}\right)=0 \]
- if we set \(z_0=\infty,z_1= 0,z_2= 1,z_3= x,z_4 = x y\), we get
\[ D(x)-D(x y)+D(y)+D\left(\frac{1-x y}{y(1-x)}\right)-D\left(\frac{1-x y}{1-x}\right) = 0 \]
- example (volume of regular ideal tetrahedron)
- \(\Delta_4\) : ideal tetrahedron with vertices \(\infty,0,1,e^{2\pi i/3}\)
- volume form on \(\mathbb{H}^3\) \[\frac{dx\,dy\,dz}{z^3}\]. So the volume of \(\Delta_4\) is
\[ \begin{aligned} \int\int\int_{\Delta_4}\frac{dx\,dy\,dz}{z^3} & = \int\int_{\Delta_3}\int_{h(x,y)}^{\infty}\frac{1}{z^3}\,dz\,dx\,dy \\ & = \int\int_{\Delta_3}\frac{1}{2h(x,y)^2}\,dx\,dy \\ \end{aligned} \]
- this integral becomes
\[ \int\int_{\Delta_3'}\frac{1}{2(\frac{1}{3}-x^2-y^2)}\,dx\,dy = 1.01494\dots \] where \(\Delta_3'\) is the triangle with vertices \(0,1,e^{2\pi i/3}\) translated so that they lie on the circle with center \((0,0)\)
메모
Bloch-Suslin
- \(B(\mathbb{F})\simeq K_3^{\operatorname{ind}}(\mathbb{F})\) ??
- \(0\to \tilde{\mu_{F}}\to K_3^{\operatorname{ind}}(\mathbb{F}) \to B(\mathbb{F})\to 0\) where \(0\to \mathbb{Z}/\mathbb{Z}_2 \to \tilde{\mu_{F}} \to \mu_{F}\to 0\) where \mu_{F} is the unit group of F
- \(K_3^{\operatorname{ind}}(\mathbb{F})\) is a quotient of Milnor K3 by something else
- functional equation of \(\zeta_K\) implies
\[ \pi^{-d_m} \lim_{s\to -m}\frac{\zeta_K(-m)}{(s+m)^{d_m}} \sim_{\mathbb{Q}^{\times}}\pi ^{-(m+1)(r_1+2 r_2)} \zeta _K(m+1)\left| d_K\right| {}^{\frac{1}{2}} \] where \(d_1 =d_3=\dots = r_2\) or \(d_2=d_4=\dots =r_1+r_2\)
- K-theory of number fields and Borel's regulator
- Bloch group
- Ideal triangulations of 3-manifolds and the Bloch invariant
- Talk on dilogarithm function and five-term relation