"콕세터 군 H4"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
(새 문서: ==개요== * 다음과 같이 정의되는 콕세터 군 $H_4$ $$ \left\langle r_1,r_2,r_3,r_4 \mid r_i^2=(r_1r_2)^5=(r_2r_3)^3=(r_3r_4)^3=(r_1r_3)^2=(r_1r_4)^2=(r_2r_4)^2=1\right\ran...)
 
 
(같은 사용자의 중간 판 2개는 보이지 않습니다)
1번째 줄: 1번째 줄:
 
==개요==
 
==개요==
−
* 다음과 같이 정의되는 콕세터 군 $H_4$
+
* 다음과 같이 정의되는 콕세터 군 <math>H_4</math>
−
$$
+
:<math>
 
\left\langle r_1,r_2,r_3,r_4 \mid r_i^2=(r_1r_2)^5=(r_2r_3)^3=(r_3r_4)^3=(r_1r_3)^2=(r_1r_4)^2=(r_2r_4)^2=1\right\rangle
 
\left\langle r_1,r_2,r_3,r_4 \mid r_i^2=(r_1r_2)^5=(r_2r_3)^3=(r_3r_4)^3=(r_1r_3)^2=(r_1r_4)^2=(r_2r_4)^2=1\right\rangle
−
$$
+
</math>
 
* 불변량
 
* 불변량
−
$$
+
:<math>
 
\begin{array}{c|ccccc}
 
\begin{array}{c|ccccc}
 
   & \text{rank} & \text{degree} & \text{exponent} & \text{order} & \text{Coxeter} \\
 
   & \text{rank} & \text{degree} & \text{exponent} & \text{order} & \text{Coxeter} \\
11번째 줄: 11번째 줄:
 
  H_4 & 4 & 2,12,20,30 & 1,11,19,29 & 14400 & 30
 
  H_4 & 4 & 2,12,20,30 & 1,11,19,29 & 14400 & 30
 
\end{array}
 
\end{array}
−
$$
+
</math>
  
  
 
==푸앵카레 다항식==
 
==푸앵카레 다항식==
−
* $W=H_4$의 푸앵카레 다항식은 다음과 같다
+
* <math>W=H_4</math>의 푸앵카레 다항식은 다음과 같다
−
$$
+
:<math>
 
\begin{aligned}
 
\begin{aligned}
 
P_{W}(q)&=\sum_{w\in W}q^{\ell(w)} \\
 
P_{W}(q)&=\sum_{w\in W}q^{\ell(w)} \\
26번째 줄: 26번째 줄:
 
&+121 q^{50}+100 q^{51}+81 q^{52}+64 q^{53}+49 q^{54}+36 q^{55}+25 q^{56}+16 q^{57}+9 q^{58}+4 q^{59}+q^{60}
 
&+121 q^{50}+100 q^{51}+81 q^{52}+64 q^{53}+49 q^{54}+36 q^{55}+25 q^{56}+16 q^{57}+9 q^{58}+4 q^{59}+q^{60}
 
\end{aligned}
 
\end{aligned}
−
$$
+
</math>
  
  
 
==콕세터 원소==
 
==콕세터 원소==
 
* 콕세터 원소의 특성다항식은 다음과 같다
 
* 콕세터 원소의 특성다항식은 다음과 같다
−
$$
+
:<math>
 
\left(-\phi +\phi ^2\right)+(1-\phi ) x+(1-\phi ) x^2+(1-\phi ) x^3+x^4
 
\left(-\phi +\phi ^2\right)+(1-\phi ) x+(1-\phi ) x^2+(1-\phi ) x^3+x^4
−
$$
+
</math>
−
여기서 $\varphi=\frac{1+\sqrt{5}}{2}$
+
여기서 <math>\varphi=\frac{1+\sqrt{5}}{2}</math>
−
* 콕세터 다항식의 해는 $\zeta, \zeta^{11},\zeta^{19},\zeta^{29}$로 주어지며 여기서 $\zeta=e^{2\pi i/30}$
+
* 콕세터 다항식의 해는 <math>\zeta, \zeta^{11},\zeta^{19},\zeta^{29}</math>로 주어지며 여기서 <math>\zeta=e^{2\pi i/30}</math>
  
  
41번째 줄: 41번째 줄:
 
* 120개의 원소로 구성
 
* 120개의 원소로 구성
 
* 다음과 같은 네 벡터가 simple system을 이룬다
 
* 다음과 같은 네 벡터가 simple system을 이룬다
−
$$
+
:<math>
 
\begin{align}
 
\begin{align}
 
r(1)=\{\alpha ,-1/2,\beta ,0\}\\
 
r(1)=\{\alpha ,-1/2,\beta ,0\}\\
48번째 줄: 48번째 줄:
 
r(4)=\{-1/2,-\alpha ,0,\beta \}
 
r(4)=\{-1/2,-\alpha ,0,\beta \}
 
\end{align}
 
\end{align}
−
$$
+
</math>
−
여기서 $\alpha=\cos \pi/5, \beta=\cos 2\pi/5$
+
여기서 <math>\alpha=\cos \pi/5, \beta=\cos 2\pi/5</math>
  
  
59번째 줄: 59번째 줄:
 
==테이블==
 
==테이블==
 
* 원소
 
* 원소
−
$$
+
:<math>
 
\begin{array}{ccc}
 
\begin{array}{ccc}
 
   & w & \ell(w) \\
 
   & w & \ell(w) \\
120번째 줄: 120번째 줄:
 
\vdots & \vdots & \vdots
 
\vdots & \vdots & \vdots
 
\end{array}
 
\end{array}
−
$$
+
</math>
  
  
136번째 줄: 136번째 줄:
 
* http://en.wikipedia.org/wiki/Binary_icosahedral_group
 
* http://en.wikipedia.org/wiki/Binary_icosahedral_group
 
[[분류:리군과 리대수]]
 
[[분류:리군과 리대수]]
 +
 +
==메타데이터==
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q4913898 Q4913898]
 +
===Spacy 패턴 목록===
 +
* [{'LOWER': 'binary'}, {'LOWER': 'icosahedral'}, {'LEMMA': 'group'}]

2021년 2월 17일 (수) 02:21 기준 최신판

개요

  • 다음과 같이 정의되는 콕세터 군 \(H_4\)

\[ \left\langle r_1,r_2,r_3,r_4 \mid r_i^2=(r_1r_2)^5=(r_2r_3)^3=(r_3r_4)^3=(r_1r_3)^2=(r_1r_4)^2=(r_2r_4)^2=1\right\rangle \]

  • 불변량

\[ \begin{array}{c|ccccc} & \text{rank} & \text{degree} & \text{exponent} & \text{order} & \text{Coxeter} \\ \hline H_4 & 4 & 2,12,20,30 & 1,11,19,29 & 14400 & 30 \end{array} \]


푸앵카레 다항식

  • \(W=H_4\)의 푸앵카레 다항식은 다음과 같다

\[ \begin{aligned} P_{W}(q)&=\sum_{w\in W}q^{\ell(w)} \\ &=1+4 q+9 q^2+16 q^3+25 q^4+36 q^5+49 q^6+64 q^7+81 q^8+100 q^9\\ &+121 q^{10}+144 q^{11}+168 q^{12}+192 q^{13}+216 q^{14}+240 q^{15}+264 q^{16}+288 q^{17}+312 q^{18}+336 q^{19}\\ &+359 q^{20}+380 q^{21}+399 q^{22}+416 q^{23}+431 q^{24}+444 q^{25}+455 q^{26}+464 q^{27}+471 q^{28}+476 q^{29}\\ &+478 q^{30}+476 q^{31}+471 q^{32}+464 q^{33}+455 q^{34}+444 q^{35}+431 q^{36}+416 q^{37}+399 q^{38}+380 q^{39}\\ &+359 q^{40}+336 q^{41}+312 q^{42}+288 q^{43}+264 q^{44}+240 q^{45}+216 q^{46}+192 q^{47}+168 q^{48}+144 q^{49}\\ &+121 q^{50}+100 q^{51}+81 q^{52}+64 q^{53}+49 q^{54}+36 q^{55}+25 q^{56}+16 q^{57}+9 q^{58}+4 q^{59}+q^{60} \end{aligned} \]


콕세터 원소

  • 콕세터 원소의 특성다항식은 다음과 같다

\[ \left(-\phi +\phi ^2\right)+(1-\phi ) x+(1-\phi ) x^2+(1-\phi ) x^3+x^4 \] 여기서 \(\varphi=\frac{1+\sqrt{5}}{2}\)

  • 콕세터 다항식의 해는 \(\zeta, \zeta^{11},\zeta^{19},\zeta^{29}\)로 주어지며 여기서 \(\zeta=e^{2\pi i/30}\)


루트 시스템

  • 120개의 원소로 구성
  • 다음과 같은 네 벡터가 simple system을 이룬다

\[ \begin{align} r(1)=\{\alpha ,-1/2,\beta ,0\}\\ r(2)=\{-\alpha ,1/2,\beta ,0\}\\ r(3)=\{1/2,\beta ,-\alpha ,0\}\\ r(4)=\{-1/2,-\alpha ,0,\beta \} \end{align} \] 여기서 \(\alpha=\cos \pi/5, \beta=\cos 2\pi/5\)


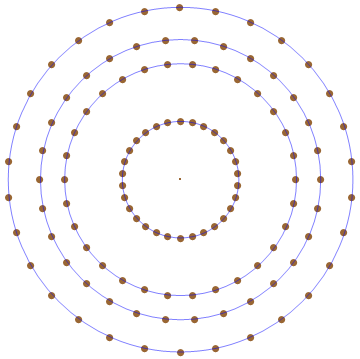
콕세터 평면으로의 사영

콕세터 군 H41.png


테이블

  • 원소

\[ \begin{array}{ccc} & w & \ell(w) \\ \hline 1 & \{\} & 0 \\ 2 & \{1\} & 1 \\ 3 & \{2\} & 1 \\ 4 & \{3\} & 1 \\ 5 & \{4\} & 1 \\ 6 & \{2,1\} & 2 \\ 7 & \{3,1\} & 2 \\ 8 & \{4,1\} & 2 \\ 9 & \{1,2\} & 2 \\ 10 & \{3,2\} & 2 \\ 11 & \{4,2\} & 2 \\ 12 & \{2,3\} & 2 \\ 13 & \{4,3\} & 2 \\ 14 & \{3,4\} & 2 \\ 15 & \{1,2,1\} & 3 \\ 16 & \{3,2,1\} & 3 \\ 17 & \{4,2,1\} & 3 \\ 18 & \{2,3,1\} & 3 \\ 19 & \{4,3,1\} & 3 \\ 20 & \{3,4,1\} & 3 \\ 21 & \{2,1,2\} & 3 \\ 22 & \{3,1,2\} & 3 \\ 23 & \{4,1,2\} & 3 \\ 24 & \{2,3,2\} & 3 \\ 25 & \{4,3,2\} & 3 \\ 26 & \{3,4,2\} & 3 \\ 27 & \{1,2,3\} & 3 \\ 28 & \{4,2,3\} & 3 \\ 29 & \{3,4,3\} & 3 \\ 30 & \{2,3,4\} & 3 \\ 31 & \{2,1,2,1\} & 4 \\ 32 & \{3,1,2,1\} & 4 \\ 33 & \{4,1,2,1\} & 4 \\ 34 & \{2,3,2,1\} & 4 \\ 35 & \{4,3,2,1\} & 4 \\ 36 & \{3,4,2,1\} & 4 \\ 37 & \{1,2,3,1\} & 4 \\ 38 & \{4,2,3,1\} & 4 \\ 39 & \{3,4,3,1\} & 4 \\ 40 & \{2,3,4,1\} & 4 \\ 41 & \{1,2,1,2\} & 4 \\ 42 & \{3,2,1,2\} & 4 \\ 43 & \{4,2,1,2\} & 4 \\ 44 & \{2,3,1,2\} & 4 \\ 45 & \{4,3,1,2\} & 4 \\ 46 & \{3,4,1,2\} & 4 \\ 47 & \{1,2,3,2\} & 4 \\ 48 & \{4,2,3,2\} & 4 \\ 49 & \{3,4,3,2\} & 4 \\ 50 & \{2,3,4,2\} & 4 \\ 51 & \{2,1,2,3\} & 4 \\ 52 & \{4,1,2,3\} & 4 \\ 53 & \{3,4,2,3\} & 4 \\ 54 & \{2,3,4,3\} & 4 \\ 55 & \{1,2,3,4\} & 4 \\ \vdots & \vdots & \vdots \end{array} \]



관련된 항목들


매스매티카 파일 및 계산 리소스


사전 형태의 자료

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'binary'}, {'LOWER': 'icosahedral'}, {'LEMMA': 'group'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=콕세터_군_H4&oldid=51987"