"사각격자의 도미노 타일링 (dimer problem)"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
(피타고라스님이 이 페이지의 dimer1(1).gif 파일을 삭제하였습니다.) |
Pythagoras0 (토론 | 기여) |
||
| (사용자 2명의 중간 판 24개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* 사각격자를 도미노로 덮는 문제 | * 사각격자를 도미노로 덮는 문제 | ||
| − | * planar bipartite graph 의 perfect matching | + | * planar bipartite graph 의 perfect matching 문제로 생각할 수 있다 |
| − | * | + | * 그래프의 적당한 weighted adjacency matrix 와 그 [[파피안(Pfaffian)]] 을 통해 답을 표현할 수 있다 |
| − | * | + | * 통계물리에서는 dimer configuration = covering of a graph by pairs of fermions connected by an edge |
| − | |||
| − | + | ==예== | |
| + | ===2x2 격자=== | ||
| + | * 다음 두 가지 경우가 존재 | ||
| + | [[파일:사각격자의 도미노 타일링 (dimer problem)1.png]] | ||
| + | * 다음 행렬의 [[파피안(Pfaffian)]] 을 구해서 경우의 수를 얻을 수 있다:<math>\left( \begin{array}{cccc} 0 & 1 & 1 & 0 \\ -1 & 0 & 0 & -1 \\ -1 & 0 & 0 & 1 \\ 0 & 1 & -1 & 0 \end{array} \right)</math> | ||
| + | * 행렬 <math>\left( \begin{array}{cccc} 0 & t_{1,2} & t_{1,3} & 0 \\ -t_{1,2} & 0 & 0 & -t_{2,4} \\ -t_{1,3} & 0 & 0 & t_{3,4} \\ 0 & t_{2,4} & -t_{3,4} & 0 \end{array} \right)</math> | ||
| + | 의 파피안은 <math>t_{1,3} t_{2,4}+t_{1,2} t_{3,4}</math> 으로 주어진다. | ||
| + | * 파피안의 각 항은 도미노 타일링에 대응된다. | ||
| − | < | + | ===3x2 격자=== |
| + | * 다음 세 가지 경우가 존재 | ||
| + | [[파일:사각격자의 도미노 타일링 (dimer problem)2.png]] | ||
| + | * 다음 행렬의 파피안은 3이다:<math>\left( \begin{array}{cccccc} 0 & 1 & 1 & 0 & 0 & 0 \\ -1 & 0 & 0 & -1 & 0 & 0 \\ -1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & -1 & 0 & 0 & -1 \\ 0 & 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 & 0 \end{array} \right)</math> | ||
| + | * 행렬 <math>\left( \begin{array}{cccccc} 0 & t_{1,2} & t_{1,3} & 0 & 0 & 0 \\ -t_{1,2} & 0 & 0 & -t_{2,4} & 0 & 0 \\ -t_{1,3} & 0 & 0 & t_{3,4} & t_{3,5} & 0 \\ 0 & t_{2,4} & -t_{3,4} & 0 & 0 & -t_{4,6} \\ 0 & 0 & -t_{3,5} & 0 & 0 & t_{5,6} \\ 0 & 0 & 0 & t_{4,6} & -t_{5,6} & 0 \end{array} \right)</math> 의 파피안은 <math>t_{1,2} t_{3,5} t_{4,6}+t_{1,3} t_{2,4} t_{5,6}+t_{1,2} t_{3,4} t_{5,6}</math> 이다. | ||
| − | |||
| − | + | ===4x4 격자=== | |
| + | * 36개의 타일링 | ||
| + | [[파일:사각격자의 도미노 타일링 (dimer problem)3.png]] | ||
| − | |||
| − | + | ==테이블== | |
| + | * <math>m\times n</math> 격자의 도미노 타일링 | ||
| + | \begin{array}{c|cccccccc} | ||
| + | m \ddots n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ | ||
| + | \hline | ||
| + | 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ | ||
| + | 2 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 \\ | ||
| + | 3 & 0 & 3 & 0 & 11 & 0 & 41 & 0 & 153 \\ | ||
| + | 4 & 1 & 5 & 11 & 36 & 95 & 281 & 781 & 2245 \\ | ||
| + | 5 & 0 & 8 & 0 & 95 & 0 & 1183 & 0 & 14824 \\ | ||
| + | 6 & 1 & 13 & 41 & 281 & 1183 & 6728 & 31529 & 167089 \\ | ||
| + | 7 & 0 & 21 & 0 & 781 & 0 & 31529 & 0 & 1292697 \\ | ||
| + | 8 & 1 & 34 & 153 & 2245 & 14824 & 167089 & 1292697 & 12988816 \\ | ||
| + | \end{array} | ||
| − | + | ==메모== | |
| − | * | + | * http://www.science.uva.nl/onderwijs/thesis/centraal/files/f887198315.pdf |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* [http://www.math.oregonstate.edu/%7Emath_reu/REU_Proceedings/Proceedings1991/Klarreich91.pdf http://www.math.oregonstate.edu/~math_reu/REU_Proceedings/Proceedings1991/Klarreich91.pdf] | * [http://www.math.oregonstate.edu/%7Emath_reu/REU_Proceedings/Proceedings1991/Klarreich91.pdf http://www.math.oregonstate.edu/~math_reu/REU_Proceedings/Proceedings1991/Klarreich91.pdf] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==관련된 항목들== | |
* [[파피안(Pfaffian)]] | * [[파피안(Pfaffian)]] | ||
| − | + | ||
| − | |||
| − | |||
| − | + | ||
| − | + | ==수학용어번역== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ==사전 형태의 자료== | |
| − | |||
| − | |||
* http://ko.wikipedia.org/wiki/ | * http://ko.wikipedia.org/wiki/ | ||
* http://en.wikipedia.org/wiki/Domino_tiling | * http://en.wikipedia.org/wiki/Domino_tiling | ||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ==리뷰논문, 에세이, 강의노트== | |
| − | + | * Borcherds [http://math.berkeley.edu/%7Ereb/courses/261/26.pdf Lecture 26 Pfaffians and dominoes] | |
| − | + | * Propp, James. “Dimers and Dominoes.” arXiv:1405.2615 [math], May 11, 2014. http://arxiv.org/abs/1405.2615. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * http:// | ||
| − | * http:// | ||
| − | |||
| − | |||
| − | + | ==관련논문== | |
| + | * Allegra, Nicolas. “<math>2d</math> Dimer Model, Correlation Functions and Combinatorics.” arXiv:1410.4131 [cond-Mat, Physics:math-Ph], October 15, 2014. http://arxiv.org/abs/1410.4131. | ||
| + | * Florescu, Laura, Daniela Morar, David Perkinson, Nick Salter, and Tianyuan Xu. “Sandpiles and Dominos.” arXiv:1406.0100 [math], May 31, 2014. http://arxiv.org/abs/1406.0100. | ||
| − | + | ||
| + | [[분류:통계물리]] | ||
| + | [[분류:조합수학]] | ||
| − | * | + | ==메타데이터== |
| − | + | ===위키데이터=== | |
| − | * | + | * ID : [https://www.wikidata.org/wiki/Q21042776 Q21042776] |
| + | ===Spacy 패턴 목록=== | ||
| + | * [{'LOWER': 'domino'}, {'LEMMA': 'tiling'}] | ||
2021년 2월 17일 (수) 04:46 기준 최신판
개요
- 사각격자를 도미노로 덮는 문제
- planar bipartite graph 의 perfect matching 문제로 생각할 수 있다
- 그래프의 적당한 weighted adjacency matrix 와 그 파피안(Pfaffian) 을 통해 답을 표현할 수 있다
- 통계물리에서는 dimer configuration = covering of a graph by pairs of fermions connected by an edge
예
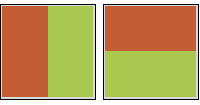
2x2 격자
- 다음 두 가지 경우가 존재
- 다음 행렬의 파피안(Pfaffian) 을 구해서 경우의 수를 얻을 수 있다\[\left( \begin{array}{cccc} 0 & 1 & 1 & 0 \\ -1 & 0 & 0 & -1 \\ -1 & 0 & 0 & 1 \\ 0 & 1 & -1 & 0 \end{array} \right)\]
- 행렬 \(\left( \begin{array}{cccc} 0 & t_{1,2} & t_{1,3} & 0 \\ -t_{1,2} & 0 & 0 & -t_{2,4} \\ -t_{1,3} & 0 & 0 & t_{3,4} \\ 0 & t_{2,4} & -t_{3,4} & 0 \end{array} \right)\)
의 파피안은 \(t_{1,3} t_{2,4}+t_{1,2} t_{3,4}\) 으로 주어진다.
- 파피안의 각 항은 도미노 타일링에 대응된다.
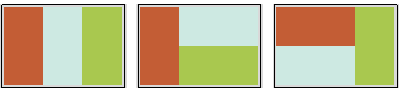
3x2 격자
- 다음 세 가지 경우가 존재
- 다음 행렬의 파피안은 3이다\[\left( \begin{array}{cccccc} 0 & 1 & 1 & 0 & 0 & 0 \\ -1 & 0 & 0 & -1 & 0 & 0 \\ -1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & -1 & 0 & 0 & -1 \\ 0 & 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 & 0 \end{array} \right)\]
- 행렬 \(\left( \begin{array}{cccccc} 0 & t_{1,2} & t_{1,3} & 0 & 0 & 0 \\ -t_{1,2} & 0 & 0 & -t_{2,4} & 0 & 0 \\ -t_{1,3} & 0 & 0 & t_{3,4} & t_{3,5} & 0 \\ 0 & t_{2,4} & -t_{3,4} & 0 & 0 & -t_{4,6} \\ 0 & 0 & -t_{3,5} & 0 & 0 & t_{5,6} \\ 0 & 0 & 0 & t_{4,6} & -t_{5,6} & 0 \end{array} \right)\) 의 파피안은 \(t_{1,2} t_{3,5} t_{4,6}+t_{1,3} t_{2,4} t_{5,6}+t_{1,2} t_{3,4} t_{5,6}\) 이다.
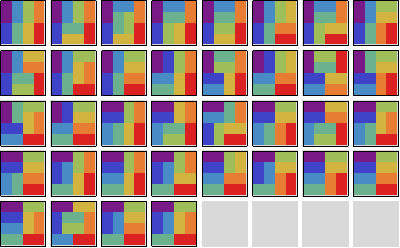
4x4 격자
- 36개의 타일링
테이블
- \(m\times n\) 격자의 도미노 타일링
\begin{array}{c|cccccccc} m \ddots n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 2 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 \\ 3 & 0 & 3 & 0 & 11 & 0 & 41 & 0 & 153 \\ 4 & 1 & 5 & 11 & 36 & 95 & 281 & 781 & 2245 \\ 5 & 0 & 8 & 0 & 95 & 0 & 1183 & 0 & 14824 \\ 6 & 1 & 13 & 41 & 281 & 1183 & 6728 & 31529 & 167089 \\ 7 & 0 & 21 & 0 & 781 & 0 & 31529 & 0 & 1292697 \\ 8 & 1 & 34 & 153 & 2245 & 14824 & 167089 & 1292697 & 12988816 \\ \end{array}
메모
- http://www.science.uva.nl/onderwijs/thesis/centraal/files/f887198315.pdf
- http://www.math.oregonstate.edu/~math_reu/REU_Proceedings/Proceedings1991/Klarreich91.pdf
관련된 항목들
수학용어번역
사전 형태의 자료
리뷰논문, 에세이, 강의노트
- Borcherds Lecture 26 Pfaffians and dominoes
- Propp, James. “Dimers and Dominoes.” arXiv:1405.2615 [math], May 11, 2014. http://arxiv.org/abs/1405.2615.
관련논문
- Allegra, Nicolas. “\(2d\) Dimer Model, Correlation Functions and Combinatorics.” arXiv:1410.4131 [cond-Mat, Physics:math-Ph], October 15, 2014. http://arxiv.org/abs/1410.4131.
- Florescu, Laura, Daniela Morar, David Perkinson, Nick Salter, and Tianyuan Xu. “Sandpiles and Dominos.” arXiv:1406.0100 [math], May 31, 2014. http://arxiv.org/abs/1406.0100.
메타데이터
위키데이터
- ID : Q21042776
Spacy 패턴 목록
- [{'LOWER': 'domino'}, {'LEMMA': 'tiling'}]