"포락선(envelope)과 curve stitching"의 두 판 사이의 차이
(피타고라스님이 이 페이지의 위치를 <a href="/pages/4909329">곡선</a>페이지로 이동하였습니다.) |
Pythagoras0 (토론 | 기여) (→메타데이터) |
||
| (사용자 2명의 중간 판 56개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | + | * "one-parameter family 에 있는 모든 곡선에 적어도 한 점에서 접하는 성질을 갖는" 곡선 | |
| + | * 이를 주어진 곡선의 family에 대한 포락선이라 부른다. | ||
| + | * 이러한 그림을 그리는 기술은 curve stitching 또는 string art 라는 이름으로 불리기도 함 | ||
| − | |||
| − | |||
| − | + | ==포락선(envelope )== | |
| − | + | * 곡선들이 매개변수 t 에 의해 <math>F(x,y,t)=0</math> 로 주어진다고 가정하자. | |
| + | * 이 곡선들에 대한 포락선은 다음 연립방정식에서 t를 소거하여 얻을 수 있다. | ||
| + | :<math>\left\{ \begin{array}{c} F(x,y,t)=0 \\ \frac{\partial F}{\partial t}(x,y,t)=0 \end{array} \right.</math> | ||
| − | + | ||
| − | + | ===증명=== | |
| − | + | 포락선이 <math>\mathbf{r}(t)=(x(t),y(t))</math> 로 매개화되었다고 하자. <math>F(x(t),y(t),t)=0</math>가 성립한다. | |
| − | + | 주어진 <math>t=t_0</math>에 대하여, 포락선의 점은 <math>\mathbf{r}(t_0)=(x(t_0),y(t_0))</math> 로 주어진다. | |
| − | + | 한편, 점 <math>(x(t_0),y(t_0))</math>에서, family의 곡선 <math>F(x,y,t_0)=0</math>에 대하여 <math>\mathbf{n}(t_0)=\langle F_{x}(x(t_0),y(t_0),t_0),F_{y}(x(t_0),y(t_0),t_0) \rangle</math>는 수직인 벡터가 된다. | |
| − | + | 따라서 <math>\mathbf{r}'(t_0)=\langle x'(t_0),y'(t_0)\rangle</math> 에 대하여 <math>\mathbf{n}(t_0)\cdot \mathbf{r}'(t_0)=F_{x}(x(t_0),y(t_0),t_0)x'(t_0)+F_{y}(x(t_0),y(t_0),t_0)y'(t_0)=0</math>이 성립한다. | |
| − | + | ||
| − | + | <math>F(x(t),y(t),t)=0</math> 의 양변을 t로 미분하면, | |
| − | + | <math>F_{x}(x(t_0),y(t_0),t_0)x'(t_0)+F_{y}(x(t_0),y(t_0),t_0)y'(t_0)+F_t(x(t_0),y(t_0),t_0)=0</math> 이므로, <math>F_t(x(t_0),y(t_0),t_0)=0</math>가 성립한다. | |
| − | + | 임의의 <math>t=t_0</math>에 대하여 성립하므로, 포락선의 매개방정식 <math>\mathbf{r}(t)=(x(t),y(t))</math>은 다음 연립방정식을 만족시킨다 | |
| + | :<math>\left\{ \begin{array}{c} F(x(t),y(t),t)=0 \\\frac{\partial F}{\partial t}(x(t),y(t),t)=0 \end{array} \right.</math> | ||
| + | ■ | ||
| − | + | ==예1== | |
| − | + | * 파라메터 t에 대하여 다음과 같은 직선들을 생각하자:<math>\frac{x}{t}+\frac{y}{10-t}=1\quad, t=1,\cdots, 9</math> | |
| − | + | [[파일:9431928-parabola1.gif]] | |
| − | + | * 그림을 보면, 이 직선들에 접하는 곡선이 나타나는 것을 관찰할 수 있다. | |
| + | * 포락선을 구하기 위해 위에서 언급한 결과를 이용하자:<math>F(x,y,t)=t^2 + t(y-x-10) + 10x</math>:<math>\frac{\partial F(x,y,t)}{\partial t}=2t+ y-x-10</math> | ||
| + | * 따라서 envelope은 다음 두 방정식에서 t를 소거함으로써 얻을 수 있다. | ||
| + | :<math>\left\{ \begin{array}{c} t^2 + t(y-x-10) + 10x=0 \\ 2t+ y-x-10=0 \end{array} \right.</math> | ||
| + | * 이로부터 <math>x^2-2 x y-20 x+y^2-20 y+100=0</math> 를 얻는다. | ||
| + | * 이는 [[이차곡선(원뿔곡선)]] 으로 판별식 <math>\Delta=b^2-4ac=4-4=0</math> 인, 포물선이 된다.[[파일:9431928-parabola2.gif]] | ||
| − | + | ||
| − | http://www.sjsu.edu/faculty/watkins/envelopetheo.htm | + | |
| + | |||
| + | ==예2: 어떤 타원들의 envelope== | ||
| + | * 파라메터 <math>0<t<1</math>에 대하여 다음과 같은 타원들이 주어진다고 하자:<math>\frac{x^2}{t^2}+\frac{y^2}{(1-t)^2}=1</math> | ||
| + | * <math>F(x,y,t)=(t-1)^2 (t-x) (t+x)-t^2 y^2</math> | ||
| + | * <math>F_{t}(x,y,t)=-2 \left(2 t^3-3 t^2-t x^2-t y^2+t+x^2\right)</math> | ||
| + | * <math>\left\{ \begin{array}{c} F(x,y,t)=0 \\ \frac{\partial F}{\partial t}(x,y,t)=0 \end{array} \right.</math> 으로부터 다음의 두 관계식을 얻을 수 있다 | ||
| + | :<math>\left\{ \begin{array}{c} y^2=(1-t)^3 \\ x^2=t^3 \end{array} \right.</math> | ||
| + | * t를 소거하면 <math>x^{2/3}+y^{2/3}=1</math> 를 얻는다. | ||
| + | * 이는 [[애스트로이드 (astroid)]] 가 된다 | ||
| + | [[파일:9431928-_envelope_curve_stitching2.gif]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==심장형 곡선== | ||
| + | |||
| + | * [[심장형 곡선(cardioid)]][[파일:10483216-심장형_곡선(cardioid)2.gif]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==메모== | ||
| + | |||
| + | * http://playingwithmathematica.com/2011/04/27/curve-stitching-with-mathematica/ | ||
| + | * http://britton.disted.camosun.bc.ca/string_art/jbstringart.htm | ||
| + | * http://www.wikihow.com/Create-a-Line-Design | ||
| + | * 베지에 곡선 | ||
| + | * http://en.wikipedia.org/wiki/B%C3%A9zier_curve#Quadratic_curves | ||
| + | * 예 | ||
| + | * parabolic line construction | ||
| + | * http://demonstrations.wolfram.com/CircleChordEnvelope/ | ||
| + | * envelope | ||
| + | * [http://en.wikipedia.org/wiki/Envelope_%28mathematics%29 http://en.wikipedia.org/wiki/Envelope_(mathematics)] | ||
| + | * http://jwilson.coe.uga.edu/Texts.Folder/Envel/envelopes.html | ||
| + | * envelope equation | ||
| + | * http://www.sjsu.edu/faculty/watkins/envelopetheo.htm | ||
| + | * Envelopes and String Art (Gregory Quenell) http://faculty.plattsburgh.edu/gregory.quenell/pubpdf/stringart.pdf | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==관련된 항목들== | ||
| + | |||
| + | * [[포물선]] | ||
| + | * [[네프로이드]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==매스매티카 파일 및 계산 리소스== | ||
| + | |||
| + | * https://docs.google.com/leaf?id=0B8XXo8Tve1cxZmVkZjZhYTItYjhlNi00ZDA4LWE4OTItMDQyMjU5Yjk5ZWMz&sort=name&layout=list&num=50 | ||
| + | |||
| + | |||
| + | |||
| + | ==수학용어번역== | ||
| + | |||
| + | |||
| + | * {{학술용어집|url=envelope}} | ||
| + | ** envelope - 포락선 | ||
| + | |||
| + | |||
| + | ==리뷰, 에세이, 강의노트== | ||
| + | * Loe, Brian J., and Nathaniel Beagley. “The Coffee Cup Caustic for Calculus Students.” The College Mathematics Journal 28, no. 4 (September 1, 1997): 277–84. doi:10.2307/2687149. | ||
| + | |||
| + | |||
| + | [[분류:곡선]] | ||
| + | [[분류:미적분학]] | ||
| + | |||
| + | == 노트 == | ||
| + | |||
| + | ===말뭉치=== | ||
| + | # The envelope of a family of curves g(x, y, c) = 0 is a curve P such that at each point of P, say (x,y), there is some member of the family that touches P tangentially.<ref name="ref_6f47d956">[https://www.sjsu.edu/faculty/watkins/envelopetheo.htm The Envelope Theorem and Its Proof]</ref> | ||
| + | # At the point of tangency the envelope curve and the corresponding curve of the family have the same slope.<ref name="ref_6f47d956" /> | ||
| + | # This is a instance of the condition that was found above for the envelope of a family of curves.<ref name="ref_6f47d956" /> | ||
| + | # The envelope of this family of curves is a curve such that at each point it touches tangentially one of the curves of the family (Figure \(1\)).<ref name="ref_d1d2702a">[https://www.math24.net/envelope-family-curves/ Envelope of a Family of Curves]</ref> | ||
| + | # Eliminating the parameter \(C\) from these equations, we can get the equation of the envelope in explicit or implicit form.<ref name="ref_d1d2702a" /> | ||
| + | # Besides the envelope curve, the solution of this system may comprise, for example, singular points of the curves of the family that do not belong to the envelope.<ref name="ref_d1d2702a" /> | ||
| + | # To find the equation of the envelope uniquely, the sufficient conditions are used.<ref name="ref_d1d2702a" /> | ||
| + | # In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope.<ref name="ref_047c8227">[https://en.wikipedia.org/wiki/Envelope_(mathematics) Envelope (mathematics)]</ref> | ||
| + | # Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves.<ref name="ref_047c8227" /> | ||
| + | # This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.<ref name="ref_047c8227" /> | ||
| + | # But these conditions are not sufficient – a given family may fail to have an envelope.<ref name="ref_047c8227" /> | ||
| + | # Example: the envelope of a circle with constant radius the centre of which describes a parabola is a curve parallel to the parabola.<ref name="ref_016241c0">[https://mathcurve.com/courbes2d.gb/enveloppe/enveloppe.shtml Envelope of a family of plane curves]</ref> | ||
| + | # The envelope can also be seen as the singular solution of the differential equation of which the curves ( G t ) are solutions.<ref name="ref_016241c0" /> | ||
| + | # Special case: the envelope of a family of lines is a curve for which this family is the family of the tangents.<ref name="ref_016241c0" /> | ||
| + | # Envelopes of lines can be physically produced thanks to tables of wires.<ref name="ref_016241c0" /> | ||
| + | # For example, two parallel lines are the envelope of the family of circles of the same radius having centres on a straight line.<ref name="ref_922e65b4">[https://www.britannica.com/science/envelope-mathematics Envelope | mathematics]</ref> | ||
| + | # My precalculus class recently returned to graphs of sinusoidal functions with an eye toward understanding them dynamically via envelope curves: Functions that bound the extreme values of the curves.<ref name="ref_403d7e79">[https://casmusings.wordpress.com/2016/05/04/envelope-curves/ Envelope Curves]</ref> | ||
| + | # Near the end is a really cool Desmos link showing an infinite progression of periodic envelopes to a single curve–totally worth the read all by itself.<ref name="ref_403d7e79" /> | ||
| + | # When you graph and its two envelope curves, you can picture the sinusoid “bouncing” between its envelopes.<ref name="ref_403d7e79" /> | ||
| + | # Those envelope functions would be just more busy work if it stopped there, though.<ref name="ref_403d7e79" /> | ||
| + | # The envelope follows the intersection of adjacent curves.<ref name="ref_c395ea06">[https://math.stackexchange.com/questions/2475863/getting-the-envelope-of-a-family-of-curves Getting the envelope of a family of curves.]</ref> | ||
| + | # The curvature theories for envelope curve of a straight line in planar motion and envelope ruled surface of a plane in spatial motion are systematically presented in differential geometry language.<ref name="ref_6ebab08a">[https://asmedigitalcollection.asme.org/mechanismsrobotics/article/7/3/031019/444981/Curvature-Theory-of-Envelope-Curve-in-Two Curvature Theory of Envelope Curve in Two-Dimensional Motion and Envelope Surface in Three-Dimensional Motion]</ref> | ||
| + | # Why cannot the long-run marginal cost curve be an envelope as well?<ref name="ref_ed7833c8">[https://www.owlgen.in/why-the-long-run-average-cost-curve-is-called-an-envelope-curve-why-cannot-the-long-run-marginal-cost-curve-be-an-envelope-as-well/ Why the Long-Run Average Cost Curve is called an Envelope Curve? Why cannot the long-run marginal cost curve be an envelope as well?]</ref> | ||
| + | # The curve long run average cost curve (LRAC) takes the scallop shape, which is why it is called an envelope curve.<ref name="ref_ed7833c8" /> | ||
| + | # As shown in the following figure, the slopes of the short-run average cost curves leads to the attainment of LRAC which is a scallop shaped which is why it is called the envelope curve.<ref name="ref_ed7833c8" /> | ||
| + | # In this paper, an envelope curve-based coverage theory (ECCT) is proposed for the rapid computation of accumulative and continuous coverage boundary during a given period.<ref name="ref_56b9f267">[https://www.sciencedirect.com/science/article/pii/S127096381932067X An envelope curve-based theory for the satellite coverage problems]</ref> | ||
| + | # First of all, the application of envelope curve theory to satellite coverage problem is introduced.<ref name="ref_56b9f267" /> | ||
| + | # Under this application background, inner envelope curves and outer envelope curves are proposed for continuous and accumulative coverage.<ref name="ref_56b9f267" /> | ||
| + | # Compactly it can be said that an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point.<ref name="ref_9c0b160a">[https://brilliant.org/wiki/envelope/ Brilliant Math & Science Wiki]</ref> | ||
| + | # Origin obtains the upper, lower, or both envelopes of the source data by applying a local maximum method combined with a cubic spline interpolation.<ref name="ref_83292947">[https://www.originlab.com/doc/Origin-Help/Envelope Envelope (Pro Only)]</ref> | ||
| + | # Professor Takashi Iwasa at Tottori University in Japan proposed a more straightforward and experimental structure method for estimating an envelope curve of wrinkled-membrane surface distortions.<ref name="ref_faa5091d">[https://advanceseng.com/envelope-curve-wrinkled-membrane-surface-distortions/ Simplified estimation method for envelope curve of wrinkled membrane surface distortions]</ref> | ||
| + | # Professor Iwasa commenced his experimental work by developing a formula for calculating the envelope curves of the membranes whose surfaces have been wrinkled due to the compressive loadings.<ref name="ref_faa5091d" /> | ||
| + | # The envelope of a set of curves is a curve C such that C is tangent to every member of the set.<ref name="ref_fb66901c">[http://xahlee.info/SpecialPlaneCurves_dir/Envelope_dir/envelope.html Envelope]</ref> | ||
| + | # The concept of envelope is easily understood by looking at its graph.<ref name="ref_fb66901c" /> | ||
| + | # When a family of curves are drawn together, their envelope takes shape.<ref name="ref_fb66901c" /> | ||
| + | # Cycloid, formed by the envelope of its tangents, and osculating circles.<ref name="ref_fb66901c" /> | ||
| + | # If you lock all envelope curves globally, they cannot be edited with the mouse.<ref name="ref_c1587d0f">[https://steinberg.help/wavelab_pro/v9.5/en/wavelab/topics/audio_montage/audio_montage_envelopes_curves_all_locking_t.html Locking All Envelope Curves]</ref> | ||
| + | # I couldn’t find an envelope curve for Australian record rainfall so made one as shown below.<ref name="ref_c9863882">[https://tonyladson.wordpress.com/2016/02/08/envelop-curve-for-record-australian-rainfall/ Envelope curve for record Australian Rainfall]</ref> | ||
| + | # The next step is to calculate the envelope curve – a straight line on a log-log plot of rainfall against duration that provides an upper bound of the record rainfall depths.<ref name="ref_c9863882" /> | ||
| + | # Record rainfalls and envelope curves are also available the world (WMO, 2009) and for New Zealand (Griffiths et al., 2014).<ref name="ref_c9863882" /> | ||
| + | # The envelope curve I proposed for Australia (the green line) looks much too steep as it crosses the world curve.<ref name="ref_c9863882" /> | ||
| + | # As you drag, the overall length of the envelope changes—with all following nodes being moved.<ref name="ref_7aac6fe8">[https://support.apple.com/guide/logicpro/use-envelope-nodes-lgsia131993/mac Use Logic Pro Sculpture envelope nodes]</ref> | ||
| + | # When you release the mouse button, the envelope display automatically zooms to show the entire envelope.<ref name="ref_7aac6fe8" /> | ||
| + | # You can, however, move nodes beyond the position of the following node—even beyond the right side of the envelope display—effectively lengthening both the envelope segment and the overall envelope.<ref name="ref_7aac6fe8" /> | ||
| + | # For example, the family of circles of the same radius with centres on a straight line has an envelope consisting of two parallel lines.<ref name="ref_28539a24">[https://encyclopediaofmath.org/wiki/Envelope Encyclopedia of Mathematics]</ref> | ||
| + | # For example, the envelope of spheres with the same radius and centres on a straight line is a cylinder.<ref name="ref_28539a24" /> | ||
| + | # The line of contact of the envelope with one of the surfaces of the family is called a characteristic.<ref name="ref_28539a24" /> | ||
| + | # I’m trying to emulate the response of the analog envelope on my Intellijel Atlantis.<ref name="ref_c7f4dfe4">[https://www.elektronauts.com/t/envelope-curve-options-which-is-closest-to-a-particular-analog-adsr/114749 Envelope curve options: which is closest to a particular analog ADSR?]</ref> | ||
| + | # Of course, I could just use the envelope on the Atlantis, but if I can do the envelope inside the A4, then I can P-lock it, have different presets ready to go, etc.<ref name="ref_c7f4dfe4" /> | ||
| + | # I’m specifically thinking of a Gaussian envelope on a TH1, so not really sophisticated.<ref name="ref_9e986871">[https://root-forum.cern.ch/t/obtaining-an-envelope-curve/25190 Obtaining an envelope curve]</ref> | ||
| + | # One adaptation of the S-curve is known as the envelope S-curve , which takes into consideration successive generations of technologies that provide the same benefits.<ref name="ref_4ecf842e">[https://www.marketingprofs.com/Tutorials/Forecast/envelopecurve.asp MarketingProfs Forecasting Tutorial]</ref> | ||
| + | # The term "envelope" refers to the curve that connects the tangents of the successive individual S-shaped curves.<ref name="ref_4ecf842e" /> | ||
| + | # Try connecting the tangents of these curves to form an "envelope" and base the forecast on the extrapolation of the envelope curve.<ref name="ref_4ecf842e" /> | ||
| + | # The dotted line represents the envelope for these two S-curves which can be used to forecast future generations of microprocessors.<ref name="ref_4ecf842e" /> | ||
| + | # Given similar basin characteristics, a peak lying close to the envelope curve might occur at other basins in the same region.<ref name="ref_daf974fd">[https://ascelibrary.org/doi/abs/10.1061/JYCEAJ.0005916 Envelope Curves for Extreme Flood Events]</ref> | ||
| + | # A method for determination of blood velocity envelopes from image data is reported that uses Doppler-data specific heuristic to achieve high accuracy and robustness.<ref name="ref_1a5e73a6">[https://www.spiedigitallibrary.org/conference-proceedings-of-spie/3979/0000/Determination-of-the-envelope-function-maximum-velocity-curve-in-Doppler/10.1117/12.387664.full Determination of the envelope function (maximum velocity curve) in Doppler ultrasound flow velocity diagrams]</ref> | ||
| + | # Comparisons with manually defined independent standards demonstrated a very good correlation in determined peak velocity values (r equals 0.993) and flow envelope areas (r equals 0.996).<ref name="ref_1a5e73a6" /> | ||
| + | # This paper tests the applicability of classic envelopes curves to the hydrological conditions of Ceará.<ref name="ref_0e94913e">[http://www.scielo.br/scielo.php?script=sci_arttext&pid=S2318-03312017000100403 Regional envelope curves for the state of Ceará: a tool for verification of hydrological dam safety]</ref> | ||
| + | # (1945) formulated another mathematical equation for the calculation of the envelope curves.<ref name="ref_0e94913e" /> | ||
| + | # Several other studies have evaluated the envelope curves as an estimator of maximum floods.<ref name="ref_0e94913e" /> | ||
| + | # (2011) used envelope curves to determine the maximum floods and their probabilities of exceedance in unmonitored basins in the state of Minas Gerais, applying the methodology of Castellarin et al.<ref name="ref_0e94913e" /> | ||
| + | ===소스=== | ||
| + | <references /> | ||
| + | |||
| + | == 메타데이터 == | ||
| + | |||
| + | ===위키데이터=== | ||
| + | * ID : [https://www.wikidata.org/wiki/Q1060372 Q1060372] | ||
| + | ===Spacy 패턴 목록=== | ||
| + | * [{'LEMMA': 'envelope'}] | ||
2021년 2월 21일 (일) 20:35 기준 최신판
개요
- "one-parameter family 에 있는 모든 곡선에 적어도 한 점에서 접하는 성질을 갖는" 곡선
- 이를 주어진 곡선의 family에 대한 포락선이라 부른다.
- 이러한 그림을 그리는 기술은 curve stitching 또는 string art 라는 이름으로 불리기도 함
포락선(envelope )
- 곡선들이 매개변수 t 에 의해 \(F(x,y,t)=0\) 로 주어진다고 가정하자.
- 이 곡선들에 대한 포락선은 다음 연립방정식에서 t를 소거하여 얻을 수 있다.
\[\left\{ \begin{array}{c} F(x,y,t)=0 \\ \frac{\partial F}{\partial t}(x,y,t)=0 \end{array} \right.\]
증명
포락선이 \(\mathbf{r}(t)=(x(t),y(t))\) 로 매개화되었다고 하자. \(F(x(t),y(t),t)=0\)가 성립한다.
주어진 \(t=t_0\)에 대하여, 포락선의 점은 \(\mathbf{r}(t_0)=(x(t_0),y(t_0))\) 로 주어진다.
한편, 점 \((x(t_0),y(t_0))\)에서, family의 곡선 \(F(x,y,t_0)=0\)에 대하여 \(\mathbf{n}(t_0)=\langle F_{x}(x(t_0),y(t_0),t_0),F_{y}(x(t_0),y(t_0),t_0) \rangle\)는 수직인 벡터가 된다.
따라서 \(\mathbf{r}'(t_0)=\langle x'(t_0),y'(t_0)\rangle\) 에 대하여 \(\mathbf{n}(t_0)\cdot \mathbf{r}'(t_0)=F_{x}(x(t_0),y(t_0),t_0)x'(t_0)+F_{y}(x(t_0),y(t_0),t_0)y'(t_0)=0\)이 성립한다.
\(F(x(t),y(t),t)=0\) 의 양변을 t로 미분하면,
\(F_{x}(x(t_0),y(t_0),t_0)x'(t_0)+F_{y}(x(t_0),y(t_0),t_0)y'(t_0)+F_t(x(t_0),y(t_0),t_0)=0\) 이므로, \(F_t(x(t_0),y(t_0),t_0)=0\)가 성립한다.
임의의 \(t=t_0\)에 대하여 성립하므로, 포락선의 매개방정식 \(\mathbf{r}(t)=(x(t),y(t))\)은 다음 연립방정식을 만족시킨다 \[\left\{ \begin{array}{c} F(x(t),y(t),t)=0 \\\frac{\partial F}{\partial t}(x(t),y(t),t)=0 \end{array} \right.\] ■
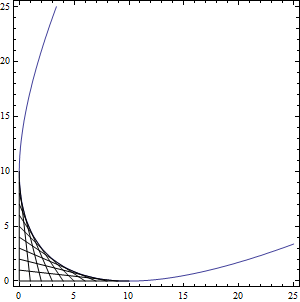
예1
- 파라메터 t에 대하여 다음과 같은 직선들을 생각하자\[\frac{x}{t}+\frac{y}{10-t}=1\quad, t=1,\cdots, 9\]
- 그림을 보면, 이 직선들에 접하는 곡선이 나타나는 것을 관찰할 수 있다.
- 포락선을 구하기 위해 위에서 언급한 결과를 이용하자\[F(x,y,t)=t^2 + t(y-x-10) + 10x\]\[\frac{\partial F(x,y,t)}{\partial t}=2t+ y-x-10\]
- 따라서 envelope은 다음 두 방정식에서 t를 소거함으로써 얻을 수 있다.
\[\left\{ \begin{array}{c} t^2 + t(y-x-10) + 10x=0 \\ 2t+ y-x-10=0 \end{array} \right.\]
- 이로부터 \(x^2-2 x y-20 x+y^2-20 y+100=0\) 를 얻는다.
- 이는 이차곡선(원뿔곡선) 으로 판별식 \(\Delta=b^2-4ac=4-4=0\) 인, 포물선이 된다.
예2: 어떤 타원들의 envelope
- 파라메터 \(0<t<1\)에 대하여 다음과 같은 타원들이 주어진다고 하자\[\frac{x^2}{t^2}+\frac{y^2}{(1-t)^2}=1\]
- \(F(x,y,t)=(t-1)^2 (t-x) (t+x)-t^2 y^2\)
- \(F_{t}(x,y,t)=-2 \left(2 t^3-3 t^2-t x^2-t y^2+t+x^2\right)\)
- \(\left\{ \begin{array}{c} F(x,y,t)=0 \\ \frac{\partial F}{\partial t}(x,y,t)=0 \end{array} \right.\) 으로부터 다음의 두 관계식을 얻을 수 있다
\[\left\{ \begin{array}{c} y^2=(1-t)^3 \\ x^2=t^3 \end{array} \right.\]
- t를 소거하면 \(x^{2/3}+y^{2/3}=1\) 를 얻는다.
- 이는 애스트로이드 (astroid) 가 된다
심장형 곡선
메모
- http://playingwithmathematica.com/2011/04/27/curve-stitching-with-mathematica/
- http://britton.disted.camosun.bc.ca/string_art/jbstringart.htm
- http://www.wikihow.com/Create-a-Line-Design
- 베지에 곡선
- http://en.wikipedia.org/wiki/B%C3%A9zier_curve#Quadratic_curves
- 예
- parabolic line construction
- http://demonstrations.wolfram.com/CircleChordEnvelope/
- envelope
- http://en.wikipedia.org/wiki/Envelope_(mathematics)
- http://jwilson.coe.uga.edu/Texts.Folder/Envel/envelopes.html
- envelope equation
- http://www.sjsu.edu/faculty/watkins/envelopetheo.htm
- Envelopes and String Art (Gregory Quenell) http://faculty.plattsburgh.edu/gregory.quenell/pubpdf/stringart.pdf
관련된 항목들
매스매티카 파일 및 계산 리소스
수학용어번역
- envelope - 대한수학회 수학용어집
- envelope - 포락선
리뷰, 에세이, 강의노트
- Loe, Brian J., and Nathaniel Beagley. “The Coffee Cup Caustic for Calculus Students.” The College Mathematics Journal 28, no. 4 (September 1, 1997): 277–84. doi:10.2307/2687149.
노트
말뭉치
- The envelope of a family of curves g(x, y, c) = 0 is a curve P such that at each point of P, say (x,y), there is some member of the family that touches P tangentially.[1]
- At the point of tangency the envelope curve and the corresponding curve of the family have the same slope.[1]
- This is a instance of the condition that was found above for the envelope of a family of curves.[1]
- The envelope of this family of curves is a curve such that at each point it touches tangentially one of the curves of the family (Figure \(1\)).[2]
- Eliminating the parameter \(C\) from these equations, we can get the equation of the envelope in explicit or implicit form.[2]
- Besides the envelope curve, the solution of this system may comprise, for example, singular points of the curves of the family that do not belong to the envelope.[2]
- To find the equation of the envelope uniquely, the sufficient conditions are used.[2]
- In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope.[3]
- Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves.[3]
- This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.[3]
- But these conditions are not sufficient – a given family may fail to have an envelope.[3]
- Example: the envelope of a circle with constant radius the centre of which describes a parabola is a curve parallel to the parabola.[4]
- The envelope can also be seen as the singular solution of the differential equation of which the curves ( G t ) are solutions.[4]
- Special case: the envelope of a family of lines is a curve for which this family is the family of the tangents.[4]
- Envelopes of lines can be physically produced thanks to tables of wires.[4]
- For example, two parallel lines are the envelope of the family of circles of the same radius having centres on a straight line.[5]
- My precalculus class recently returned to graphs of sinusoidal functions with an eye toward understanding them dynamically via envelope curves: Functions that bound the extreme values of the curves.[6]
- Near the end is a really cool Desmos link showing an infinite progression of periodic envelopes to a single curve–totally worth the read all by itself.[6]
- When you graph and its two envelope curves, you can picture the sinusoid “bouncing” between its envelopes.[6]
- Those envelope functions would be just more busy work if it stopped there, though.[6]
- The envelope follows the intersection of adjacent curves.[7]
- The curvature theories for envelope curve of a straight line in planar motion and envelope ruled surface of a plane in spatial motion are systematically presented in differential geometry language.[8]
- Why cannot the long-run marginal cost curve be an envelope as well?[9]
- The curve long run average cost curve (LRAC) takes the scallop shape, which is why it is called an envelope curve.[9]
- As shown in the following figure, the slopes of the short-run average cost curves leads to the attainment of LRAC which is a scallop shaped which is why it is called the envelope curve.[9]
- In this paper, an envelope curve-based coverage theory (ECCT) is proposed for the rapid computation of accumulative and continuous coverage boundary during a given period.[10]
- First of all, the application of envelope curve theory to satellite coverage problem is introduced.[10]
- Under this application background, inner envelope curves and outer envelope curves are proposed for continuous and accumulative coverage.[10]
- Compactly it can be said that an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point.[11]
- Origin obtains the upper, lower, or both envelopes of the source data by applying a local maximum method combined with a cubic spline interpolation.[12]
- Professor Takashi Iwasa at Tottori University in Japan proposed a more straightforward and experimental structure method for estimating an envelope curve of wrinkled-membrane surface distortions.[13]
- Professor Iwasa commenced his experimental work by developing a formula for calculating the envelope curves of the membranes whose surfaces have been wrinkled due to the compressive loadings.[13]
- The envelope of a set of curves is a curve C such that C is tangent to every member of the set.[14]
- The concept of envelope is easily understood by looking at its graph.[14]
- When a family of curves are drawn together, their envelope takes shape.[14]
- Cycloid, formed by the envelope of its tangents, and osculating circles.[14]
- If you lock all envelope curves globally, they cannot be edited with the mouse.[15]
- I couldn’t find an envelope curve for Australian record rainfall so made one as shown below.[16]
- The next step is to calculate the envelope curve – a straight line on a log-log plot of rainfall against duration that provides an upper bound of the record rainfall depths.[16]
- Record rainfalls and envelope curves are also available the world (WMO, 2009) and for New Zealand (Griffiths et al., 2014).[16]
- The envelope curve I proposed for Australia (the green line) looks much too steep as it crosses the world curve.[16]
- As you drag, the overall length of the envelope changes—with all following nodes being moved.[17]
- When you release the mouse button, the envelope display automatically zooms to show the entire envelope.[17]
- You can, however, move nodes beyond the position of the following node—even beyond the right side of the envelope display—effectively lengthening both the envelope segment and the overall envelope.[17]
- For example, the family of circles of the same radius with centres on a straight line has an envelope consisting of two parallel lines.[18]
- For example, the envelope of spheres with the same radius and centres on a straight line is a cylinder.[18]
- The line of contact of the envelope with one of the surfaces of the family is called a characteristic.[18]
- I’m trying to emulate the response of the analog envelope on my Intellijel Atlantis.[19]
- Of course, I could just use the envelope on the Atlantis, but if I can do the envelope inside the A4, then I can P-lock it, have different presets ready to go, etc.[19]
- I’m specifically thinking of a Gaussian envelope on a TH1, so not really sophisticated.[20]
- One adaptation of the S-curve is known as the envelope S-curve , which takes into consideration successive generations of technologies that provide the same benefits.[21]
- The term "envelope" refers to the curve that connects the tangents of the successive individual S-shaped curves.[21]
- Try connecting the tangents of these curves to form an "envelope" and base the forecast on the extrapolation of the envelope curve.[21]
- The dotted line represents the envelope for these two S-curves which can be used to forecast future generations of microprocessors.[21]
- Given similar basin characteristics, a peak lying close to the envelope curve might occur at other basins in the same region.[22]
- A method for determination of blood velocity envelopes from image data is reported that uses Doppler-data specific heuristic to achieve high accuracy and robustness.[23]
- Comparisons with manually defined independent standards demonstrated a very good correlation in determined peak velocity values (r equals 0.993) and flow envelope areas (r equals 0.996).[23]
- This paper tests the applicability of classic envelopes curves to the hydrological conditions of Ceará.[24]
- (1945) formulated another mathematical equation for the calculation of the envelope curves.[24]
- Several other studies have evaluated the envelope curves as an estimator of maximum floods.[24]
- (2011) used envelope curves to determine the maximum floods and their probabilities of exceedance in unmonitored basins in the state of Minas Gerais, applying the methodology of Castellarin et al.[24]
소스
- ↑ 1.0 1.1 1.2 The Envelope Theorem and Its Proof
- ↑ 2.0 2.1 2.2 2.3 Envelope of a Family of Curves
- ↑ 3.0 3.1 3.2 3.3 Envelope (mathematics)
- ↑ 4.0 4.1 4.2 4.3 Envelope of a family of plane curves
- ↑ Envelope | mathematics
- ↑ 6.0 6.1 6.2 6.3 Envelope Curves
- ↑ Getting the envelope of a family of curves.
- ↑ Curvature Theory of Envelope Curve in Two-Dimensional Motion and Envelope Surface in Three-Dimensional Motion
- ↑ 9.0 9.1 9.2 Why the Long-Run Average Cost Curve is called an Envelope Curve? Why cannot the long-run marginal cost curve be an envelope as well?
- ↑ 10.0 10.1 10.2 An envelope curve-based theory for the satellite coverage problems
- ↑ Brilliant Math & Science Wiki
- ↑ Envelope (Pro Only)
- ↑ 13.0 13.1 Simplified estimation method for envelope curve of wrinkled membrane surface distortions
- ↑ 14.0 14.1 14.2 14.3 Envelope
- ↑ Locking All Envelope Curves
- ↑ 16.0 16.1 16.2 16.3 Envelope curve for record Australian Rainfall
- ↑ 17.0 17.1 17.2 Use Logic Pro Sculpture envelope nodes
- ↑ 18.0 18.1 18.2 Encyclopedia of Mathematics
- ↑ 19.0 19.1 Envelope curve options: which is closest to a particular analog ADSR?
- ↑ Obtaining an envelope curve
- ↑ 21.0 21.1 21.2 21.3 MarketingProfs Forecasting Tutorial
- ↑ Envelope Curves for Extreme Flood Events
- ↑ 23.0 23.1 Determination of the envelope function (maximum velocity curve) in Doppler ultrasound flow velocity diagrams
- ↑ 24.0 24.1 24.2 24.3 Regional envelope curves for the state of Ceará: a tool for verification of hydrological dam safety
메타데이터
위키데이터
- ID : Q1060372
Spacy 패턴 목록
- [{'LEMMA': 'envelope'}]


