"원환면 (torus)"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) 잔글 (찾아 바꾸기 – “<br><math>” 문자열을 “:<math>” 문자열로) |
Pythagoras0 (토론 | 기여) |
||
| (같은 사용자의 중간 판 2개는 보이지 않습니다) | |||
| 11번째 줄: | 11번째 줄: | ||
* 매개화 | * 매개화 | ||
| − | * <math>X(u,v)=\{\cos (u) (a+b \cos (v)),\sin (u) (a+b \cos (v)),b \sin (v)\}</math>:<math>0<u<2\pi</math>, <math>0<v<2\pi</math | + | * <math>X(u,v)=\{\cos (u) (a+b \cos (v)),\sin (u) (a+b \cos (v)),b \sin (v)\}</math>:<math>0<u<2\pi</math>, <math>0<v<2\pi</math> |
| − | * <math>X_u=\{\sin (u) (-(a+b \cos (v))),\cos (u) (a+b \cos (v)),0\}</math>:<math>X_v=\{-b \cos (u) \sin (v),-b \sin (u) \sin (v),b \cos (v)\}</math | + | * <math>X_u=\{\sin (u) (-(a+b \cos (v))),\cos (u) (a+b \cos (v)),0\}</math>:<math>X_v=\{-b \cos (u) \sin (v),-b \sin (u) \sin (v),b \cos (v)\}</math> |
* <math>N=\{b \cos (u) \cos (v) (a+b \cos (v)),b \sin (u) \cos (v) (a+b \cos (v)),b \sin (v) (a+b \cos (v))\}</math> | * <math>N=\{b \cos (u) \cos (v) (a+b \cos (v)),b \sin (u) \cos (v) (a+b \cos (v)),b \sin (v) (a+b \cos (v))\}</math> | ||
| − | * 왼쪽 그림의 붉은 색 작은 원을 y-축에 대하여 회전하여, 오른쪽 원환면을 얻는다 | + | * 왼쪽 그림의 붉은 색 작은 원을 y-축에 대하여 회전하여, 오른쪽 원환면을 얻는다 [[파일:원환면 (torus)1.gif]] -> [[파일:원환면 (torus)2.gif]] |
| 36번째 줄: | 36번째 줄: | ||
==크리스토펠 기호== | ==크리스토펠 기호== | ||
| − | * [[크리스토펠 기호]] 항목 참조:<math>\Gamma^1_{11}=0</math>:<math>\Gamma^1_{12}=-\frac{b \sin (v)}{a+b \cos (v)}</math>:<math>\Gamma^1_{21}=-\frac{b \sin (v)}{a+b \cos (v)}</math>:<math>\Gamma^1_{22}=0</math>:<math>\Gamma^2_{11}=\frac{\sin (v) (a+b \cos (v))}{b}</math>:<math>\Gamma^2_{12}=0</math>:<math>\Gamma^2_{21}=0</math>:<math>\Gamma^2_{22}=0</math | + | * [[크리스토펠 기호]] 항목 참조:<math>\Gamma^1_{11}=0</math>:<math>\Gamma^1_{12}=-\frac{b \sin (v)}{a+b \cos (v)}</math>:<math>\Gamma^1_{21}=-\frac{b \sin (v)}{a+b \cos (v)}</math>:<math>\Gamma^1_{22}=0</math>:<math>\Gamma^2_{11}=\frac{\sin (v) (a+b \cos (v))}{b}</math>:<math>\Gamma^2_{12}=0</math>:<math>\Gamma^2_{21}=0</math>:<math>\Gamma^2_{22}=0</math> |
| 44번째 줄: | 44번째 줄: | ||
==측지선== | ==측지선== | ||
| − | * [[측지선]] 이 만족시키는 미분방정식:<math>\frac{d^2\alpha_k }{dt^2} + \Gamma^{k}_{~i j }\frac{d\alpha_i }{dt}\frac{d\alpha_j }{dt} = 0</math | + | * [[측지선]] 이 만족시키는 미분방정식:<math>\frac{d^2\alpha_k }{dt^2} + \Gamma^{k}_{~i j }\frac{d\alpha_i }{dt}\frac{d\alpha_j }{dt} = 0</math> |
| − | * 풀어쓰면, :<math>\frac{d^2 u}{dt^2} -\frac{2b \sin (v)}{a+b \cos (v)}\frac{du }{dt}\frac{dv }{dt} = 0</math>:<math>\frac{d^2 v}{dt^2} + \frac{\sin (v) (a+b \cos (v))}{b}\frac{du }{dt}\frac{du }{dt} = 0</math | + | * 풀어쓰면, :<math>\frac{d^2 u}{dt^2} -\frac{2b \sin (v)}{a+b \cos (v)}\frac{du }{dt}\frac{dv }{dt} = 0</math>:<math>\frac{d^2 v}{dt^2} + \frac{\sin (v) (a+b \cos (v))}{b}\frac{du }{dt}\frac{du }{dt} = 0</math> |
| 53번째 줄: | 53번째 줄: | ||
==가우스곡률== | ==가우스곡률== | ||
| − | * [[가우스 곡률|가우스곡률]] 항목 참조:<math>K = -\frac{1}{2\sqrt{EG}}\left(\frac{\partial}{\partial u}\frac{G_u}{\sqrt{EG}} + \frac{\partial}{\partial v}\frac{E_v}{\sqrt{EG}}\right)=\frac{\cos (v)}{a b+b^2 \cos (v)}</math | + | * [[가우스 곡률|가우스곡률]] 항목 참조:<math>K = -\frac{1}{2\sqrt{EG}}\left(\frac{\partial}{\partial u}\frac{G_u}{\sqrt{EG}} + \frac{\partial}{\partial v}\frac{E_v}{\sqrt{EG}}\right)=\frac{\cos (v)}{a b+b^2 \cos (v)}</math> |
| 64번째 줄: | 64번째 줄: | ||
* http://www.google.com/search?hl=en&tbs=tl:1&q= | * http://www.google.com/search?hl=en&tbs=tl:1&q= | ||
| − | * [[ | + | * [[수학사 연표]] |
| 89번째 줄: | 89번째 줄: | ||
==매스매티카 파일 및 계산 리소스== | ==매스매티카 파일 및 계산 리소스== | ||
| − | + | * https://drive.google.com/file/d/0B8XXo8Tve1cxMDVmNGMxNzYtMjM5NC00ZWIwLWEwMzYtMGIwOWEwNTUwZDg0/view | |
| − | * https:// | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==리뷰논문, 에세이, 강의노트== | ==리뷰논문, 에세이, 강의노트== | ||
2020년 11월 12일 (목) 21:22 기준 최신판
개요
매개화
- 매개화
- \(X(u,v)=\{\cos (u) (a+b \cos (v)),\sin (u) (a+b \cos (v)),b \sin (v)\}\)\[0<u<2\pi\], \(0<v<2\pi\)
- \(X_u=\{\sin (u) (-(a+b \cos (v))),\cos (u) (a+b \cos (v)),0\}\)\[X_v=\{-b \cos (u) \sin (v),-b \sin (u) \sin (v),b \cos (v)\}\]
- \(N=\{b \cos (u) \cos (v) (a+b \cos (v)),b \sin (u) \cos (v) (a+b \cos (v)),b \sin (v) (a+b \cos (v))\}\)
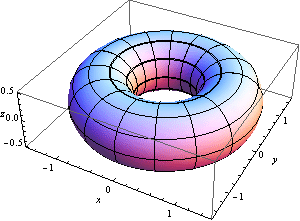
- 왼쪽 그림의 붉은 색 작은 원을 y-축에 대하여 회전하여, 오른쪽 원환면을 얻는다
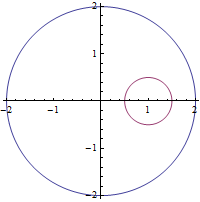 ->
-> 
제1기본형식
- \(E=(a+b \cos (v))^2\)
- \(F=0\)
- \(G=b^2\)
크리스토펠 기호
- 크리스토펠 기호 항목 참조\[\Gamma^1_{11}=0\]\[\Gamma^1_{12}=-\frac{b \sin (v)}{a+b \cos (v)}\]\[\Gamma^1_{21}=-\frac{b \sin (v)}{a+b \cos (v)}\]\[\Gamma^1_{22}=0\]\[\Gamma^2_{11}=\frac{\sin (v) (a+b \cos (v))}{b}\]\[\Gamma^2_{12}=0\]\[\Gamma^2_{21}=0\]\[\Gamma^2_{22}=0\]
측지선
- 측지선 이 만족시키는 미분방정식\[\frac{d^2\alpha_k }{dt^2} + \Gamma^{k}_{~i j }\frac{d\alpha_i }{dt}\frac{d\alpha_j }{dt} = 0\]
- 풀어쓰면, \[\frac{d^2 u}{dt^2} -\frac{2b \sin (v)}{a+b \cos (v)}\frac{du }{dt}\frac{dv }{dt} = 0\]\[\frac{d^2 v}{dt^2} + \frac{\sin (v) (a+b \cos (v))}{b}\frac{du }{dt}\frac{du }{dt} = 0\]
가우스곡률
- 가우스곡률 항목 참조\[K = -\frac{1}{2\sqrt{EG}}\left(\frac{\partial}{\partial u}\frac{G_u}{\sqrt{EG}} + \frac{\partial}{\partial v}\frac{E_v}{\sqrt{EG}}\right)=\frac{\cos (v)}{a b+b^2 \cos (v)}\]
역사
메모
- Math Overflow http://mathoverflow.net/search?q=
관련된 항목들