"Nested radicals"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
 
(같은 사용자의 중간 판 8개는 보이지 않습니다)
1번째 줄: 1번째 줄:
 
==개요==
 
==개요==
  
−
* [[황금비]]:<math>\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}}=\varphi=\frac{1+\sqrt5}{2}=1.61803398874989\cdots</math><br>
+
* [[황금비]]:<math>\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}}=\varphi=\frac{1+\sqrt5}{2}=1.61803398874989\cdots</math>
−
* [[비에타의 공식]]:<math>\frac{2}{\pi}=\frac{\sqrt{2}}{2}\frac{\sqrt{2+\sqrt{2}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}}{2}\cdots</math><br>
+
* [[비에타의 공식]]:<math>\frac{2}{\pi}=\frac{\sqrt{2}}{2}\frac{\sqrt{2+\sqrt{2}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}}{2}\cdots</math>
−
*  nested radical 상수:<math>\sqrt{1+\sqrt{2+\sqrt{3+\sqrt{4+\sqrt{5+\sqrt{6+\cdots}}}}}}=1.75793275661800453270881963821820816125\cdots</math><br>
+
*  nested radical 상수:<math>\sqrt{1+\sqrt{2+\sqrt{3+\sqrt{4+\sqrt{5+\sqrt{6+\cdots}}}}}}=1.75793275661800453270881963821820816125\cdots</math>
−
*  삼각함수의 값:<math>\cos \frac{\pi}{32}=\cos\frac{\pi}{2^5}=  \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2}</math>:<math>\cos \frac{\pi}{64}=\cos\frac{\pi}{2^6}= \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}{2}</math><br>
+
*  삼각함수의 값:<math>\cos \frac{\pi}{32}=\cos\frac{\pi}{2^5}=  \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2}</math>:<math>\cos \frac{\pi}{64}=\cos\frac{\pi}{2^6}= \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}{2}</math>
  
−
 
+
  
−
 
+
  
 
==라마누잔이 제시한 문제==
 
==라마누잔이 제시한 문제==
26번째 줄: 26번째 줄:
  
 
===함수방정식===
 
===함수방정식===
−
* $f(x)=\sqrt{1+x \sqrt{1+(x+1) \sqrt{1+(x+2) \sqrt{\cdots}}}}$
+
* <math>f(x)=\sqrt{1+x \sqrt{1+(x+1) \sqrt{1+(x+2) \sqrt{\cdots}}}}</math>
−
* $[f(x)]^2=1+xf(x+1), f(x)\ge 0$
+
* <math>[f(x)]^2=1+xf(x+1), f(x)\ge 0</math>
−
* $f(x)=x+1$
+
* <math>f(x)=x+1</math>
 
* Functional Equations and and How to Solve Them, Section 3.8 Functional equations and nested radicals
 
* Functional Equations and and How to Solve Them, Section 3.8 Functional equations and nested radicals
  
36번째 줄: 36번째 줄:
 
;증명
 
;증명
  
−
먼저 수렴성을 증명하자. 다음과 같이 정의된 수열 
+
먼저 수렴성을 증명하자. 다음과 같이 정의된 수열
  
 
<math>1,\sqrt{1+2 },\sqrt{1+2 \sqrt{1+3 }},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 }}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 }}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 }}}}}, \cdots</math> 은 위로 유계이다.
 
<math>1,\sqrt{1+2 },\sqrt{1+2 \sqrt{1+3 }},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 }}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 }}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 }}}}}, \cdots</math> 은 위로 유계이다.
  
−
 
+
  
 
<math>\sqrt{1+2 \sqrt{1+3\sqrt{1+\cdots+ (n-1)\sqrt{1+n} }}} \leq \sqrt{1+2 \sqrt{1+3\sqrt{1+\cdots+ (n-1)\sqrt{1+n(n+2)} }}}=3</math>
 
<math>\sqrt{1+2 \sqrt{1+3\sqrt{1+\cdots+ (n-1)\sqrt{1+n} }}} \leq \sqrt{1+2 \sqrt{1+3\sqrt{1+\cdots+ (n-1)\sqrt{1+n(n+2)} }}}=3</math>
  
−
 
+
  
 
<math>n=\sqrt{1+(n-1)(n+1)}</math>을 이용
 
<math>n=\sqrt{1+(n-1)(n+1)}</math>을 이용
50번째 줄: 50번째 줄:
 
<math>\begin{eqnarray*}3 &=& \sqrt{1+2\cdot4}\\ &=& \sqrt{1+2\sqrt{1+3\cdot5}}\\ &=& \sqrt{1+2\sqrt{1+3\sqrt{1+4\cdot6}}}\\ &=& \cdots\end{eqnarray*}</math>
 
<math>\begin{eqnarray*}3 &=& \sqrt{1+2\cdot4}\\ &=& \sqrt{1+2\sqrt{1+3\cdot5}}\\ &=& \sqrt{1+2\sqrt{1+3\sqrt{1+4\cdot6}}}\\ &=& \cdots\end{eqnarray*}</math>
  
−
 
+
  
  
  
 
==메모==
 
==메모==
−
 
+
* http://math.stackexchange.com/questions/435778/finding-the-value-of-sqrt12-sqrt23-sqrt34-sqrt45-sqrt5-dots
 
* [http://www.dgp.toronto.edu/%7Emjmcguff/math/nestedRadicals.pdf http://www.dgp.toronto.edu/~mjmcguff/math/nestedRadicals.pdf]
 
* [http://www.dgp.toronto.edu/%7Emjmcguff/math/nestedRadicals.pdf http://www.dgp.toronto.edu/~mjmcguff/math/nestedRadicals.pdf]
 
* http://fluxionsdividebyzero.com/p1/math/calculus/number/cr/sr_nroots.pdf
 
* http://fluxionsdividebyzero.com/p1/math/calculus/number/cr/sr_nroots.pdf
−
* http://math.stackexchange.com/questions/435778/finding-the-value-of-sqrt12-sqrt23-sqrt34-sqrt45-sqrt5-dots
+
−
 
 
−
 
 
−
 
 
  
 
==관련된 항목들==
 
==관련된 항목들==
67번째 줄: 64번째 줄:
 
* [[연분수와 유리수 근사|연분수]]
 
* [[연분수와 유리수 근사|연분수]]
  
−
 
+
 
==매스매티카 파일 및 계산 리소스==
 
==매스매티카 파일 및 계산 리소스==
 
* https://docs.google.com/file/d/0B8XXo8Tve1cxU1hvM09SaThwN0E/edit
 
* https://docs.google.com/file/d/0B8XXo8Tve1cxU1hvM09SaThwN0E/edit
−
 
+
* http://mathematica.stackexchange.com/questions/100591/how-to-evaluate-the-limit-of-a-function-consists-of-range
 +
* http://oeis.org/A072449
 +
 
  
 
==관련도서==
 
==관련도서==
 +
* https://books.google.com.au/books?id=TT1T8A94xNcC&pg=PA221&redir_esc=y#v=onepage&q&f=false
 
* Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000.
 
* Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000.
 
* Functional Equations and and How to Solve Them
 
* Functional Equations and and How to Solve Them
 
** section 3.8
 
** section 3.8
  
−
 
+
−
 
 
−
 
 
  
 
==관련논문==
 
==관련논문==
 +
* Campbell, Geoffrey B., and Aleksander Zujev. “Variations on Ramanujan’s Nested Radicals.” arXiv:1511.06865 [math], November 21, 2015. http://arxiv.org/abs/1511.06865.
 
* Herschfeld, Aaron. 1935. “On Infinite Radicals.” The American Mathematical Monthly 42 (7) (August 1): 419–429. doi:http://dx.doi.org/10.2307/2301294.
 
* Herschfeld, Aaron. 1935. “On Infinite Radicals.” The American Mathematical Monthly 42 (7) (August 1): 419–429. doi:http://dx.doi.org/10.2307/2301294.
 
* Ramanujan, S. Question No. 298. J. Indian Math. Soc. 1911.
 
* Ramanujan, S. Question No. 298. J. Indian Math. Soc. 1911.
  
−
 
+
  
−
 
+
  
 
==사전형태의 참고자료==
 
==사전형태의 참고자료==
95번째 줄: 94번째 줄:
  
  
−
 
+
  
 
==블로그==
 
==블로그==
  
 
* [http://hshin.info/ New Start, Ens!], 2009-1-16 [http://hshin.info/173 Ramanujan's infinitely nested radicals problem]
 
* [http://hshin.info/ New Start, Ens!], 2009-1-16 [http://hshin.info/173 Ramanujan's infinitely nested radicals problem]
 +
 +
==메타데이터==
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q2670069 Q2670069]
 +
===Spacy 패턴 목록===
 +
* [{'LOWER': 'nested'}, {'LEMMA': 'radical'}]

2021년 2월 17일 (수) 03:49 기준 최신판

개요

  • 황금비\[\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}}=\varphi=\frac{1+\sqrt5}{2}=1.61803398874989\cdots\]
  • 비에타의 공식\[\frac{2}{\pi}=\frac{\sqrt{2}}{2}\frac{\sqrt{2+\sqrt{2}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}}{2}\cdots\]
  • nested radical 상수\[\sqrt{1+\sqrt{2+\sqrt{3+\sqrt{4+\sqrt{5+\sqrt{6+\cdots}}}}}}=1.75793275661800453270881963821820816125\cdots\]
  • 삼각함수의 값\[\cos \frac{\pi}{32}=\cos\frac{\pi}{2^5}= \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2}\]\[\cos \frac{\pi}{64}=\cos\frac{\pi}{2^6}= \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}{2}\]



라마누잔이 제시한 문제

  • 다음 수열의 극한

\[1,\sqrt{1+2 },\sqrt{1+2 \sqrt{1+3 }},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 }}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 }}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 }}}}}, \cdots\]

정리

\(\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+5\sqrt{1+6\cdots}}}}} = 3\)


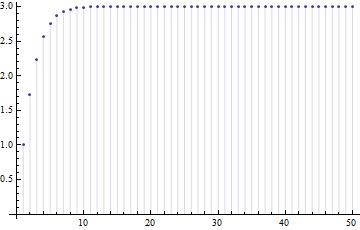
수열의 크기 변화

\(1,\sqrt{1+2 },\sqrt{1+2 \sqrt{1+3 }},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 }}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 }}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 }}}}}, \cdots\)

2529712-nested radicals.jpg


함수방정식

  • \(f(x)=\sqrt{1+x \sqrt{1+(x+1) \sqrt{1+(x+2) \sqrt{\cdots}}}}\)
  • \([f(x)]^2=1+xf(x+1), f(x)\ge 0\)
  • \(f(x)=x+1\)
  • Functional Equations and and How to Solve Them, Section 3.8 Functional equations and nested radicals



증명

먼저 수렴성을 증명하자. 다음과 같이 정의된 수열

\(1,\sqrt{1+2 },\sqrt{1+2 \sqrt{1+3 }},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 }}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 }}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 }}}}}, \cdots\) 은 위로 유계이다.


\(\sqrt{1+2 \sqrt{1+3\sqrt{1+\cdots+ (n-1)\sqrt{1+n} }}} \leq \sqrt{1+2 \sqrt{1+3\sqrt{1+\cdots+ (n-1)\sqrt{1+n(n+2)} }}}=3\)


\(n=\sqrt{1+(n-1)(n+1)}\)을 이용

\(\begin{eqnarray*}3 &=& \sqrt{1+2\cdot4}\\ &=& \sqrt{1+2\sqrt{1+3\cdot5}}\\ &=& \sqrt{1+2\sqrt{1+3\sqrt{1+4\cdot6}}}\\ &=& \cdots\end{eqnarray*}\)



메모


관련된 항목들


매스매티카 파일 및 계산 리소스


관련도서


관련논문

  • Campbell, Geoffrey B., and Aleksander Zujev. “Variations on Ramanujan’s Nested Radicals.” arXiv:1511.06865 [math], November 21, 2015. http://arxiv.org/abs/1511.06865.
  • Herschfeld, Aaron. 1935. “On Infinite Radicals.” The American Mathematical Monthly 42 (7) (August 1): 419–429. doi:http://dx.doi.org/10.2307/2301294.
  • Ramanujan, S. Question No. 298. J. Indian Math. Soc. 1911.



사전형태의 참고자료



블로그

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'nested'}, {'LEMMA': 'radical'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=Nested_radicals&oldid=52140"