"교차비(cross ratio)"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
|||
| (사용자 2명의 중간 판 13개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==교차비== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* 사영기하학의 기본개념 | * 사영기하학의 기본개념 | ||
| − | * 네 | + | * 네 복소수 <math>z_1,z_2,z_3,z_4</math>에 대하여 다음과 같이 정의됨. |
| + | :<math>(z_1,z_2;z_3,z_4) = \frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)}</math> | ||
| + | * <math>z_4=\infty</math> 인 경우 | ||
| + | :<math>(z_1,z_2;z_3,\infty) = \frac{(z_1-z_3)}{(z_2-z_3)}</math> | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ==대칭군과 교차비== | |
| + | * [[대칭군 (symmetric group)]]은 <math>\{1,2,3,4\}</math>에 작용한다 | ||
| + | * 조화비의 isotopy group은 다음과 같이 주어진다 | ||
| + | :<math> | ||
| + | \left\{\left( | ||
| + | \begin{array}{cccc} | ||
| + | 1 & 2 & 3 & 4 \\ | ||
| + | 1 & 2 & 3 & 4 | ||
| + | \end{array} | ||
| + | \right),\left( | ||
| + | \begin{array}{cccc} | ||
| + | 1 & 2 & 3 & 4 \\ | ||
| + | 2 & 1 & 4 & 3 | ||
| + | \end{array} | ||
| + | \right),\left( | ||
| + | \begin{array}{cccc} | ||
| + | 1 & 2 & 3 & 4 \\ | ||
| + | 3 & 4 & 1 & 2 | ||
| + | \end{array} | ||
| + | \right),\left( | ||
| + | \begin{array}{cccc} | ||
| + | 1 & 2 & 3 & 4 \\ | ||
| + | 4 & 3 & 2 & 1 | ||
| + | \end{array} | ||
| + | \right)\right\} | ||
| + | </math> | ||
| + | 즉 <math>(z_1,z_2;z_3,z_4)=(z_2,z_1;z_4,z_3)=(z_3,z_4;z_1,z_2)=(z_4,z_3;z_2,z_1)</math> | ||
| + | * 조화비는 <math>S_4</math>의 작용에 의해 다음과 같이 변화한다 | ||
| + | :<math>(z_1, z_2; z_3, z_4) = \lambda</math> | ||
| + | :<math>(z_1, z_2; z_4, z_3) = {1\over\lambda}</math> | ||
| + | :<math>(z_1, z_3; z_4, z_2) = {1\over{1-\lambda}}</math> | ||
| + | :<math>(z_1, z_3; z_2, z_4) = 1-\lambda</math> | ||
| + | :<math>(z_1, z_4; z_3, z_2) = {\lambda\over{\lambda-1}}</math> | ||
| + | :<math>(z_1, z_4; z_2, z_3) = {{\lambda-1}\over\lambda}</math> | ||
| + | * 즉 대칭군에 의해 다음 값을 가질 수 있다 | ||
| + | :<math> \lambda, {1\over\lambda},{1\over{1-\lambda}}, 1-\lambda, {\lambda\over{\lambda-1}}, {{\lambda-1}\over\lambda}</math> | ||
| − | + | ||
| − | + | ||
| − | * [[ | + | ==사영기하학과 교차비== |
| − | + | * [[뫼비우스 변환]]이 네 점, <math>z_1,z_2,z_3,z_4</math> 를 <math>w_1,w_2,w_3,w_4</math>로 보내는 경우, 교차비는 보존됨. | |
| − | + | :<math>\frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)} = \frac{(w_1-w_3)(w_2-w_4)}{(w_2-w_3)(w_1-w_4)}</math> | |
| + | 즉 <math>ad-bc\neq 0</math>일 때, | ||
| + | :<math> | ||
| + | \frac{\left(z_1-z_3\right) \left(z_2-z_4\right)}{\left(z_2-z_3\right) \left(z_1-z_4\right)}= | ||
| + | \frac{\left(\frac{a z_1+b}{c z_1+d}-\frac{a z_3+b}{c z_3+d}\right) \left(\frac{a z_2+b}{c z_2+d}-\frac{a z_4+b}{c z_4+d}\right)}{\left(\frac{a z_2+b}{c z_2+d}-\frac{a z_3+b}{c z_3+d}\right) \left(\frac{a z_1+b}{c z_1+d}-\frac{a z_4+b}{c z_4+d}\right)} | ||
| + | </math> | ||
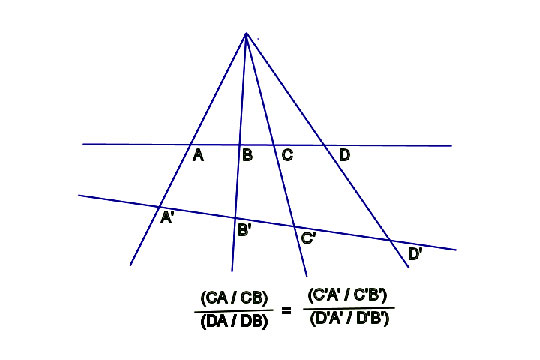
| + | * 교차비는 사영기하학의 불변량이다 | ||
| + | [[파일:3259985-afigure006-riemann65.jpg]] | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ==관련된 항목들== | |
| − | + | * [[뫼비우스 변환군과 기하학]] | |
| + | * [[타원 모듈라 λ-함수]] | ||
| + | * [[다이로그 함수(dilogarithm)]] | ||
| + | * [[원근법과 수학]] | ||
| − | + | ||
| − | + | ||
| − | + | ==매스매티카 파일 및 계산 리소스== | |
| − | * | + | * https://docs.google.com/leaf?id=0B8XXo8Tve1cxY2Y4OWEwNWMtMGU0Zi00NTEwLTlkYjctZWE3NDE0YTA2YmM2&sort=name&layout=list&num=50 |
| − | * | + | * http://mathworld.wolfram.com/CrossRatio.html |
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | + | ==수학용어번역== | |
| + | * {{학술용어집|url=cross}} | ||
| + | ** cross ratio | ||
| + | ** 비조화비, 복비 | ||
| + | |||
| − | + | ==사전 형태의 자료== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* http://ko.wikipedia.org/wiki/ | * http://ko.wikipedia.org/wiki/ | ||
* http://en.wikipedia.org/wiki/cross_ratio | * http://en.wikipedia.org/wiki/cross_ratio | ||
| − | + | [[분류:복소함수론]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | + | ==메타데이터== |
| − | * | + | ===위키데이터=== |
| + | * ID : [https://www.wikidata.org/wiki/Q899539 Q899539] | ||
| + | ===Spacy 패턴 목록=== | ||
| + | * [{'LOWER': 'cross'}, {'LOWER': '-'}, {'LEMMA': 'ratio'}] | ||
2021년 2월 17일 (수) 03:59 기준 최신판
교차비
- 사영기하학의 기본개념
- 네 복소수 \(z_1,z_2,z_3,z_4\)에 대하여 다음과 같이 정의됨.
\[(z_1,z_2;z_3,z_4) = \frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)}\]
- \(z_4=\infty\) 인 경우
\[(z_1,z_2;z_3,\infty) = \frac{(z_1-z_3)}{(z_2-z_3)}\]
대칭군과 교차비
- 대칭군 (symmetric group)은 \(\{1,2,3,4\}\)에 작용한다
- 조화비의 isotopy group은 다음과 같이 주어진다
\[ \left\{\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 2 & 3 & 4 \end{array} \right),\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \end{array} \right),\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 1 & 2 \end{array} \right),\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{array} \right)\right\} \] 즉 \((z_1,z_2;z_3,z_4)=(z_2,z_1;z_4,z_3)=(z_3,z_4;z_1,z_2)=(z_4,z_3;z_2,z_1)\)
- 조화비는 \(S_4\)의 작용에 의해 다음과 같이 변화한다
\[(z_1, z_2; z_3, z_4) = \lambda\] \[(z_1, z_2; z_4, z_3) = {1\over\lambda}\] \[(z_1, z_3; z_4, z_2) = {1\over{1-\lambda}}\] \[(z_1, z_3; z_2, z_4) = 1-\lambda\] \[(z_1, z_4; z_3, z_2) = {\lambda\over{\lambda-1}}\] \[(z_1, z_4; z_2, z_3) = {{\lambda-1}\over\lambda}\]
- 즉 대칭군에 의해 다음 값을 가질 수 있다
\[ \lambda, {1\over\lambda},{1\over{1-\lambda}}, 1-\lambda, {\lambda\over{\lambda-1}}, {{\lambda-1}\over\lambda}\]
사영기하학과 교차비
- 뫼비우스 변환이 네 점, \(z_1,z_2,z_3,z_4\) 를 \(w_1,w_2,w_3,w_4\)로 보내는 경우, 교차비는 보존됨.
\[\frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)} = \frac{(w_1-w_3)(w_2-w_4)}{(w_2-w_3)(w_1-w_4)}\] 즉 \(ad-bc\neq 0\)일 때, \[ \frac{\left(z_1-z_3\right) \left(z_2-z_4\right)}{\left(z_2-z_3\right) \left(z_1-z_4\right)}= \frac{\left(\frac{a z_1+b}{c z_1+d}-\frac{a z_3+b}{c z_3+d}\right) \left(\frac{a z_2+b}{c z_2+d}-\frac{a z_4+b}{c z_4+d}\right)}{\left(\frac{a z_2+b}{c z_2+d}-\frac{a z_3+b}{c z_3+d}\right) \left(\frac{a z_1+b}{c z_1+d}-\frac{a z_4+b}{c z_4+d}\right)} \]
- 교차비는 사영기하학의 불변량이다
관련된 항목들
매스매티카 파일 및 계산 리소스
- https://docs.google.com/leaf?id=0B8XXo8Tve1cxY2Y4OWEwNWMtMGU0Zi00NTEwLTlkYjctZWE3NDE0YTA2YmM2&sort=name&layout=list&num=50
- http://mathworld.wolfram.com/CrossRatio.html
수학용어번역
- cross - 대한수학회 수학용어집
- cross ratio
- 비조화비, 복비
사전 형태의 자료
메타데이터
위키데이터
- ID : Q899539
Spacy 패턴 목록
- [{'LOWER': 'cross'}, {'LOWER': '-'}, {'LEMMA': 'ratio'}]