"렘니스케이트 곡선의 등분 (Lemniscatomy)"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) 잔글 (찾아 바꾸기 – “==관련도서== * 도서내검색<br> ** http://books.google.com/books?q= ** http://book.daum.net/search/contentSearch.do?query=” 문자열을 “” 문자열로) |
Pythagoras0 (토론 | 기여) |
||
| (같은 사용자의 중간 판 10개는 보이지 않습니다) | |||
| 7번째 줄: | 7번째 줄: | ||
==렘니스케이트 사인과 코사인== | ==렘니스케이트 사인과 코사인== | ||
| − | * 렘니스케이트 사인 | + | * 렘니스케이트 사인:<math>x=\int_{0}^{s}\frac{dx}{\sqrt{1-x^4}}</math> |
| − | * 렘니스케이트 코사인 | + | * 렘니스케이트 코사인:<math>x=\int_{c}^{1}\frac{dx}{\sqrt{1-x^4}}</math> |
| − | * 관계식 | + | * 관계식:<math>s (x)^2+c (x)^2+c (x)^2 s (x)^2=1</math> |
| − | * 덧셈공식 | + | * 덧셈공식:<math>s(x+y)=\frac{s(x) c(y)+c(x) s(y)}{1-s(x) c(x) s(y) c(y)}</math> |
| 20번째 줄: | 20번째 줄: | ||
* 렘니스케이트 사인함수 <math>x=\phi(t)</math>는 타원적분 <math>t=\int_{0}^{x}\frac{dx}{\sqrt{1-x^4}}</math> 의 역함수로 정의된다 | * 렘니스케이트 사인함수 <math>x=\phi(t)</math>는 타원적분 <math>t=\int_{0}^{x}\frac{dx}{\sqrt{1-x^4}}</math> 의 역함수로 정의된다 | ||
* <math>m\in\mathbb{Z}[i]</math> 에 대하여, <math>y=\phi(mt)</math> 로 두면, <math>mt=\int_{0}^{y}\frac{dy}{\sqrt{1-y^4}}</math> 을 만족한다 | * <math>m\in\mathbb{Z}[i]</math> 에 대하여, <math>y=\phi(mt)</math> 로 두면, <math>mt=\int_{0}^{y}\frac{dy}{\sqrt{1-y^4}}</math> 을 만족한다 | ||
| − | * <math>x=\phi(t)</math>와 <math>y=\phi(mt)</math>는 | + | * <math>x=\phi(t)</math>와 <math>y=\phi(mt)</math>는:<math>\frac{dy}{\sqrt{1-y^4}}=m\frac{dx}{\sqrt{1-x^4}}</math> 의 관계를 만족한다 |
| − | * 렘니스케이트 사인함수의 덧셈공식 | + | * 렘니스케이트 사인함수의 덧셈공식(파그나노의 공식) |
| − | * <math>\phi(z)</math> 는 다음 [[자코비 타원함수]] 와 같다 | + | :<math>\phi(t+t')=\frac{\phi(t)\sqrt{1-\phi(t')^4}+\phi(t')\sqrt{1-\phi(t)^4}}{1+\phi(t)^2\phi(t')^2}</math> |
| + | * <math>\phi(z)</math> 는 다음 [[자코비 타원함수]] 와 같다:<math>\text{sn}(z|-1)=z-\frac{z^5}{10}+\frac{z^9}{120}-\frac{11 z^{13}}{15600}+\frac{211 z^{17}}{3536000}+O\left(z^{21}\right)</math> | ||
| + | ;정리 | ||
| + | 홀수인 가우스 정수 <math>m=a+bi\in \mathbb{Z}[i]</math>를 생각하자. 적당한 <math>A_i\in \mathbb{Z}[i]</math>가 존재하여 다음을 만족한다 | ||
| + | :<math> | ||
| + | \phi(m\alpha)=i^{\epsilon}\phi\frac{\phi^{p-1}+A_1\phi^{p-5}+\cdots+A_{(p-1)/4}}{1+A_1\phi^{4}+\cdots+A_{(p-1)/4}\phi^{p-1}} \label{aa} | ||
| + | </math> | ||
| + | 여기서 <math>\epsilon\in \{0,1,2,3\}</math>은 <math>m-i^{\epsilon}\in (2)</math>를 만족, <math>\phi=\phi(\alpha)</math>이고, <math>p=a^2+b^2</math>. | ||
| + | |||
| + | ;정리 (아이젠슈타인) | ||
| + | 홀수인 가우스 정수 <math>m=a+bi\in \mathbb{Z}[i]</math>이 소수일 때, \ref{aa}의 <math>A_1,\cdots, A_{(p-1)/4}</math>는 <math>m</math>으로 나누어진다. | ||
| − | |||
| − | == | + | ==렘니스케이트 곡선의 등분== |
* 삼각함수의 [[삼각함수의 배각공식 표|삼각함수의 배각공식]] 에 비유하면 적당하다 | * 삼각함수의 [[삼각함수의 배각공식 표|삼각함수의 배각공식]] 에 비유하면 적당하다 | ||
| 35번째 줄: | 44번째 줄: | ||
| − | + | ===3등분점=== | |
| − | |||
| − | ==3등분점== | ||
| − | * | + | * 타원함수의 변환 |
| + | :<math>\phi(3\alpha)=-\phi\frac{\phi^8+6\phi^4-3}{1+6\phi^4-3\phi^8},\, \phi:=\phi(\alpha)</math> | ||
* 위의 식으로부터 <math>\phi^8+6\phi^4-3=0</math> 의 해를 구하면, 렘니스케이트의 삼등분점을 구할 수 있다 | * 위의 식으로부터 <math>\phi^8+6\phi^4-3=0</math> 의 해를 구하면, 렘니스케이트의 삼등분점을 구할 수 있다 | ||
[[파일:렘니스케이트 곡선과 Lemniscatomy1.gif]] | [[파일:렘니스케이트 곡선과 Lemniscatomy1.gif]] | ||
| − | * 세 점의 좌표는 다음과 같이 주어진다 | + | * 세 점의 좌표는 다음과 같이 주어진다:<math>\left(0,0\right)</math>:<math>\left(\sqrt{\frac{1}{2} \left(1+\sqrt{-3+2 \sqrt{3}}\right)},\sqrt{\frac{1}{2} \left(1-\sqrt{-3+2 \sqrt{3}}\right)}\right)</math>:<math>\left(\sqrt{\frac{1}{2} \left(1+\sqrt{-3+2 \sqrt{3}}\right)},-\sqrt{\frac{1}{2} \left(1-\sqrt{-3+2 \sqrt{3}}\right)}\right)</math> |
| − | ==5등분점== | + | ===5등분점=== |
| + | * 타원함수의 변환 | ||
| + | :<math> | ||
| + | \phi(5\alpha)=\frac{\phi \left(5-62 \phi ^4-105 \phi ^8+300 \phi ^{12}-125 \phi ^{16}+50 \phi ^{20}+\phi ^{24}\right)}{1+50 \phi ^4-125 \phi ^8+300 \phi ^{12}-105 \phi ^{16}-62 \phi ^{20}+5 \phi ^{24}},\, \phi:=\phi(\alpha) | ||
| + | </math> | ||
[[파일:렘니스케이트 곡선과 Lemniscatomy2.gif]] | [[파일:렘니스케이트 곡선과 Lemniscatomy2.gif]] | ||
:<math>\left(\frac{\left(-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}\right)^{1/4} \sqrt{1+\sqrt{-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}}}}{\sqrt{2}},\frac{\left(-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}\right)^{1/4} \sqrt{1-\sqrt{-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}}}}{\sqrt{2}}\right)</math> | :<math>\left(\frac{\left(-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}\right)^{1/4} \sqrt{1+\sqrt{-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}}}}{\sqrt{2}},\frac{\left(-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}\right)^{1/4} \sqrt{1-\sqrt{-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}}}}{\sqrt{2}}\right)</math> | ||
| − | + | ||
| − | + | ||
==역사== | ==역사== | ||
| 59번째 줄: | 71번째 줄: | ||
* 1827 아벨 | * 1827 아벨 | ||
* 1846 아이젠슈타인 | * 1846 아이젠슈타인 | ||
| − | + | * [[수학사 연표]] | |
| − | * [[ | ||
| 68번째 줄: | 79번째 줄: | ||
==메모== | ==메모== | ||
| − | * http://books.google.com/books?id=9xu_fuIhmnYC&pg=PA46&lpg=PA46&dq=lemniscate+sine+cosine&source=bl&ots=sSXXD0v-DD&sig=9DA4Q26OtTQAyNVM_saqcJvQRP4&hl=en&sa=X&ei=K9YFUJTPF4nI2AXhneStBQ&ved=0CE4Q6AEwAA # v=onepage&q=lemniscate % | + | * http://books.google.com/books?id=9xu_fuIhmnYC&pg=PA46&lpg=PA46&dq=lemniscate+sine+cosine&source=bl&ots=sSXXD0v-DD&sig=9DA4Q26OtTQAyNVM_saqcJvQRP4&hl=en&sa=X&ei=K9YFUJTPF4nI2AXhneStBQ&ved=0CE4Q6AEwAA#v=onepage&q=lemniscate%20sine%20cosine&f=false |
| − | * http://books.google.com/books?id=3u4RF8SrRooC&pg=PA459&lpg=PA459&dq=lemniscate+division+cyclotomic&source=bl&ots=JpHeSPRYpp&sig=pFs13_v-R5n62_BideWx-31j7Gw&hl=ko&sa=X&ei=koZGT6rUAbGPigLw4MXbDQ&ved=0CCcQ6AEwAA # v=onepage&q=lemniscate % | + | * http://books.google.com/books?id=3u4RF8SrRooC&pg=PA459&lpg=PA459&dq=lemniscate+division+cyclotomic&source=bl&ots=JpHeSPRYpp&sig=pFs13_v-R5n62_BideWx-31j7Gw&hl=ko&sa=X&ei=koZGT6rUAbGPigLw4MXbDQ&ved=0CCcQ6AEwAA#v=onepage&q=lemniscate%20division%20cyclotomic&f=false |
* Norbert Schappacher, [http://www-irma.u-strasbg.fr/%7Eschappa/NSch/Publications_files/Lemnis.pdf Some Milestones of Lemniscatomy] | * Norbert Schappacher, [http://www-irma.u-strasbg.fr/%7Eschappa/NSch/Publications_files/Lemnis.pdf Some Milestones of Lemniscatomy] | ||
* David A. Cox, "[http://www.cs.amherst.edu/%7Edac/normat.pdf Why Eisenstein proved the Eisenstein Criterion and why Schönemann discovered it first]", American Mathematical Monthly 118 Vol 1 (January 2011) | * David A. Cox, "[http://www.cs.amherst.edu/%7Edac/normat.pdf Why Eisenstein proved the Eisenstein Criterion and why Schönemann discovered it first]", American Mathematical Monthly 118 Vol 1 (January 2011) | ||
| − | |||
| − | |||
| − | |||
| 82번째 줄: | 90번째 줄: | ||
* [[렘니스케이트(lemniscate) 곡선의 길이와 타원적분]] | * [[렘니스케이트(lemniscate) 곡선의 길이와 타원적분]] | ||
* [[자코비 타원함수]] | * [[자코비 타원함수]] | ||
| + | * [[가우스 정수]] | ||
* [[complex multiplication]] | * [[complex multiplication]] | ||
| 89번째 줄: | 98번째 줄: | ||
==수학용어번역== | ==수학용어번역== | ||
| − | * | + | * lemniscatomy |
| − | * | + | * cyclotomy |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
==매스매티카 파일 및 계산 리소스== | ==매스매티카 파일 및 계산 리소스== | ||
* https://docs.google.com/file/d/0B8XXo8Tve1cxc1JxdlNPUjBleEE/edit | * https://docs.google.com/file/d/0B8XXo8Tve1cxc1JxdlNPUjBleEE/edit | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==리뷰논문, 에세이, 강의노트== | ==리뷰논문, 에세이, 강의노트== | ||
| − | + | ||
| − | + | ||
| − | + | ||
==관련논문== | ==관련논문== | ||
* N.H. Abel (1827–28), Recherches sur les fonctions elliptiques, Journal f.d. reine & angew. Math. 2, 101–181, 3, 160–190 [ = OEuvres compl`etes (Sylow, Lie, ed.s), vol. I, pp. 263–388] | * N.H. Abel (1827–28), Recherches sur les fonctions elliptiques, Journal f.d. reine & angew. Math. 2, 101–181, 3, 160–190 [ = OEuvres compl`etes (Sylow, Lie, ed.s), vol. I, pp. 263–388] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | |||
| + | |||
| + | [[분류:타원적분]] | ||
2020년 12월 28일 (월) 02:17 기준 최신판
개요
렘니스케이트 사인과 코사인
- 렘니스케이트 사인\[x=\int_{0}^{s}\frac{dx}{\sqrt{1-x^4}}\]
- 렘니스케이트 코사인\[x=\int_{c}^{1}\frac{dx}{\sqrt{1-x^4}}\]
- 관계식\[s (x)^2+c (x)^2+c (x)^2 s (x)^2=1\]
- 덧셈공식\[s(x+y)=\frac{s(x) c(y)+c(x) s(y)}{1-s(x) c(x) s(y) c(y)}\]
렘니스케이트 타원함수
- 렘니스케이트 사인함수 \(x=\phi(t)\)는 타원적분 \(t=\int_{0}^{x}\frac{dx}{\sqrt{1-x^4}}\) 의 역함수로 정의된다
- \(m\in\mathbb{Z}[i]\) 에 대하여, \(y=\phi(mt)\) 로 두면, \(mt=\int_{0}^{y}\frac{dy}{\sqrt{1-y^4}}\) 을 만족한다
- \(x=\phi(t)\)와 \(y=\phi(mt)\)는\[\frac{dy}{\sqrt{1-y^4}}=m\frac{dx}{\sqrt{1-x^4}}\] 의 관계를 만족한다
- 렘니스케이트 사인함수의 덧셈공식(파그나노의 공식)
\[\phi(t+t')=\frac{\phi(t)\sqrt{1-\phi(t')^4}+\phi(t')\sqrt{1-\phi(t)^4}}{1+\phi(t)^2\phi(t')^2}\]
- \(\phi(z)\) 는 다음 자코비 타원함수 와 같다\[\text{sn}(z|-1)=z-\frac{z^5}{10}+\frac{z^9}{120}-\frac{11 z^{13}}{15600}+\frac{211 z^{17}}{3536000}+O\left(z^{21}\right)\]
- 정리
홀수인 가우스 정수 \(m=a+bi\in \mathbb{Z}[i]\)를 생각하자. 적당한 \(A_i\in \mathbb{Z}[i]\)가 존재하여 다음을 만족한다 \[ \phi(m\alpha)=i^{\epsilon}\phi\frac{\phi^{p-1}+A_1\phi^{p-5}+\cdots+A_{(p-1)/4}}{1+A_1\phi^{4}+\cdots+A_{(p-1)/4}\phi^{p-1}} \label{aa} \] 여기서 \(\epsilon\in \{0,1,2,3\}\)은 \(m-i^{\epsilon}\in (2)\)를 만족, \(\phi=\phi(\alpha)\)이고, \(p=a^2+b^2\).
- 정리 (아이젠슈타인)
홀수인 가우스 정수 \(m=a+bi\in \mathbb{Z}[i]\)이 소수일 때, \ref{aa}의 \(A_1,\cdots, A_{(p-1)/4}\)는 \(m\)으로 나누어진다.
렘니스케이트 곡선의 등분
- 삼각함수의 삼각함수의 배각공식 에 비유하면 적당하다
- 렘니스케이트 타원함수의 덧셈공식으로부터 유도할 수 있다
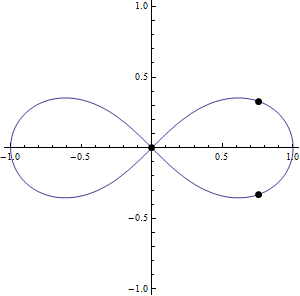
3등분점
- 타원함수의 변환
\[\phi(3\alpha)=-\phi\frac{\phi^8+6\phi^4-3}{1+6\phi^4-3\phi^8},\, \phi:=\phi(\alpha)\]
- 위의 식으로부터 \(\phi^8+6\phi^4-3=0\) 의 해를 구하면, 렘니스케이트의 삼등분점을 구할 수 있다
- 세 점의 좌표는 다음과 같이 주어진다\[\left(0,0\right)\]\[\left(\sqrt{\frac{1}{2} \left(1+\sqrt{-3+2 \sqrt{3}}\right)},\sqrt{\frac{1}{2} \left(1-\sqrt{-3+2 \sqrt{3}}\right)}\right)\]\[\left(\sqrt{\frac{1}{2} \left(1+\sqrt{-3+2 \sqrt{3}}\right)},-\sqrt{\frac{1}{2} \left(1-\sqrt{-3+2 \sqrt{3}}\right)}\right)\]
5등분점
- 타원함수의 변환
\[
\phi(5\alpha)=\frac{\phi \left(5-62 \phi ^4-105 \phi ^8+300 \phi ^{12}-125 \phi ^{16}+50 \phi ^{20}+\phi ^{24}\right)}{1+50 \phi ^4-125 \phi ^8+300 \phi ^{12}-105 \phi ^{16}-62 \phi ^{20}+5 \phi ^{24}},\, \phi:=\phi(\alpha)
\]
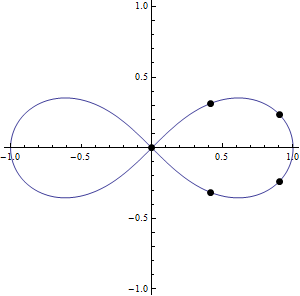
\[\left(\frac{\left(-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}\right)^{1/4} \sqrt{1+\sqrt{-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}}}}{\sqrt{2}},\frac{\left(-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}\right)^{1/4} \sqrt{1-\sqrt{-13+6 \sqrt{5}-2 \sqrt{85-38 \sqrt{5}}}}}{\sqrt{2}}\right)\]
역사
- 1797 가우스
- 1827 아벨
- 1846 아이젠슈타인
- 수학사 연표
메모
- http://books.google.com/books?id=9xu_fuIhmnYC&pg=PA46&lpg=PA46&dq=lemniscate+sine+cosine&source=bl&ots=sSXXD0v-DD&sig=9DA4Q26OtTQAyNVM_saqcJvQRP4&hl=en&sa=X&ei=K9YFUJTPF4nI2AXhneStBQ&ved=0CE4Q6AEwAA#v=onepage&q=lemniscate%20sine%20cosine&f=false
- http://books.google.com/books?id=3u4RF8SrRooC&pg=PA459&lpg=PA459&dq=lemniscate+division+cyclotomic&source=bl&ots=JpHeSPRYpp&sig=pFs13_v-R5n62_BideWx-31j7Gw&hl=ko&sa=X&ei=koZGT6rUAbGPigLw4MXbDQ&ved=0CCcQ6AEwAA#v=onepage&q=lemniscate%20division%20cyclotomic&f=false
- Norbert Schappacher, Some Milestones of Lemniscatomy
- David A. Cox, "Why Eisenstein proved the Eisenstein Criterion and why Schönemann discovered it first", American Mathematical Monthly 118 Vol 1 (January 2011)
관련된 항목들
수학용어번역
- lemniscatomy
- cyclotomy
매스매티카 파일 및 계산 리소스
리뷰논문, 에세이, 강의노트
관련논문
- N.H. Abel (1827–28), Recherches sur les fonctions elliptiques, Journal f.d. reine & angew. Math. 2, 101–181, 3, 160–190 [ = OEuvres compl`etes (Sylow, Lie, ed.s), vol. I, pp. 263–388]