"사다리타기의 수학"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
|||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* 제비뽑기에 사용되는 도구 | * 제비뽑기에 사용되는 도구 | ||
| − | * 수학적으로 각각의 사다리는 [[대칭군 (symmetric group)]] | + | * 수학적으로 각각의 사다리는 [[대칭군 (symmetric group)]] 의 원소와 일대일대응된다 |
| − | + | ||
| − | + | ||
| − | + | ==대칭군과의 관계== | |
* 세 사람이 등장하는 사다리의 경우<br> | * 세 사람이 등장하는 사다리의 경우<br> | ||
| − | * 다음 두 사다리는, 아무 것도 없는 경우와 같다 | + | * 다음 두 사다리는, 아무 것도 없는 경우와 같다 |
| + | [[파일:사다리타기의 수학1.gif]] [[파일:사다리타기의 수학2.gif]] | ||
* 다음 두 사다리는 같은 결과를 준다 | * 다음 두 사다리는 같은 결과를 준다 | ||
| + | [[파일:사다리타기의 수학3.gif]] [[파일:사다리타기의 수학4.gif]] | ||
* 위의 사실들은 [[대칭군 (symmetric group)]] 의 생성원들 사이에 성립하는 다음 관계와 대응된다 (<math>\sigma_i=(i, i+1)</math> 라 하자)<br> | * 위의 사실들은 [[대칭군 (symmetric group)]] 의 생성원들 사이에 성립하는 다음 관계와 대응된다 (<math>\sigma_i=(i, i+1)</math> 라 하자)<br> | ||
** <math>{\sigma_i}^2 = 1</math> | ** <math>{\sigma_i}^2 = 1</math> | ||
| − | ** <math>\sigma_i\sigma_{i+1}\sigma_i = \sigma_{i+1}\sigma_i\sigma_{i+1} | + | ** <math>\sigma_i\sigma_{i+1}\sigma_i = \sigma_{i+1}\sigma_i\sigma_{i+1}</math> (또는 <math>(\sigma_i\sigma_{i+1})^3=1</math> 로 쓸 수 있다) |
| − | |||
| − | + | ||
| − | + | ||
| − | + | ==역사== | |
| − | + | ||
* http://www.google.com/search?hl=en&tbs=tl:1&q= | * http://www.google.com/search?hl=en&tbs=tl:1&q= | ||
* [[수학사연표 (역사)|수학사연표]] | * [[수학사연표 (역사)|수학사연표]] | ||
| − | + | ||
| − | + | ||
| − | + | ==메모== | |
* Ladders, Codes, and Actions | * Ladders, Codes, and Actions | ||
2012년 10월 18일 (목) 12:49 판
개요
- 제비뽑기에 사용되는 도구
- 수학적으로 각각의 사다리는 대칭군 (symmetric group) 의 원소와 일대일대응된다
대칭군과의 관계
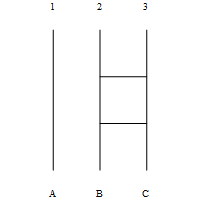
- 세 사람이 등장하는 사다리의 경우
- 다음 두 사다리는, 아무 것도 없는 경우와 같다
- 다음 두 사다리는 같은 결과를 준다
- 위의 사실들은 대칭군 (symmetric group) 의 생성원들 사이에 성립하는 다음 관계와 대응된다 (\(\sigma_i=(i, i+1)\) 라 하자)
- \({\sigma_i}^2 = 1\)
- \(\sigma_i\sigma_{i+1}\sigma_i = \sigma_{i+1}\sigma_i\sigma_{i+1}\) (또는 \((\sigma_i\sigma_{i+1})^3=1\) 로 쓸 수 있다)
역사
메모
- Ladders, Codes, and Actions
- http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=2684
- http://blog.naver.com/PostView.nhn?blogId=artkishan&logNo=140000659705
- http://www2.edc.org/makingmath/studentWork/amidaKuji/AmidaKujiByDavidSenft.pdf
- Math Overflow http://mathoverflow.net/search?q=
관련된 항목들
매스매티카 파일 및 계산 리소스
- https://docs.google.com/leaf?id=0B8XXo8Tve1cxYWIwYzI5MDctZmE1OC00MmQwLWI3MjEtZmIyMzBhN2VlNjBm&sort=name&layout=list&num=50
- http://www.wolframalpha.com/input/?i=
- http://functions.wolfram.com/
- NIST Digital Library of Mathematical Functions
- Abramowitz and Stegun Handbook of mathematical functions
- The On-Line Encyclopedia of Integer Sequences
- Numbers, constants and computation
- 매스매티카 파일 목록
수학용어번역
- 단어사전
- 발음사전 http://www.forvo.com/search/
- 대한수학회 수학 학술 용어집
- 한국통계학회 통계학 용어 온라인 대조표
- 남·북한수학용어비교
- 대한수학회 수학용어한글화 게시판
사전 형태의 자료
- http://en.wikipedia.org/wiki/Ghost_Leg
- The Online Encyclopaedia of Mathematics
- NIST Digital Library of Mathematical Functions
- The World of Mathematical Equations
리뷰논문, 에세이, 강의노트
관련논문