"최단시간강하곡선 문제(Brachistochrone problem)"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| 1번째 줄: | 1번째 줄: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==개요== | ==개요== | ||
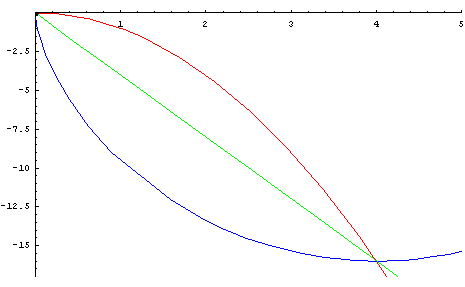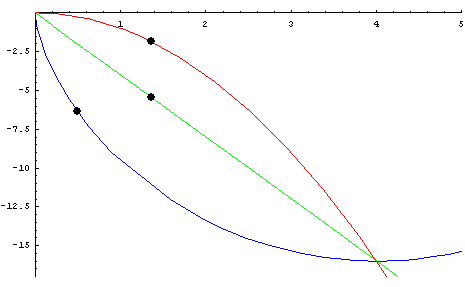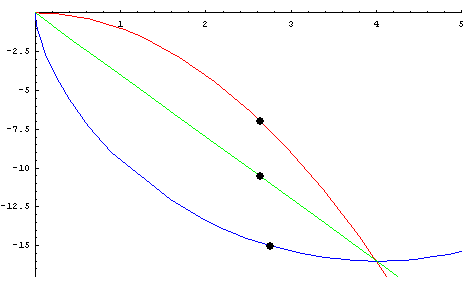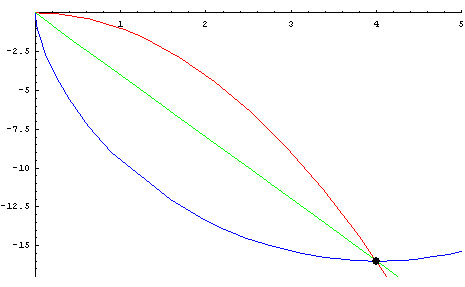
* 중력을 받고 있는 물체가 정지상태에서 출발하여 가장 짧은 시간내에 하강하기 위해서 따라야 하는 곡선 | * 중력을 받고 있는 물체가 정지상태에서 출발하여 가장 짧은 시간내에 하강하기 위해서 따라야 하는 곡선 | ||
| − | * | + | * 1697년에 베르누이에 의하여 답이 출판 |
| − | + | [[파일:4402517-ParabNickF.gif]] | |
| − | |||
| − | [http://books.google.com/books?id=dptKVr-5LJAC&pg=PA223&sig=PVA7Q1U_MyXinobyhOf54BwjShQ&hl=en#v=onepage&q&f=false ] | + | [http://books.google.com/books?id=dptKVr-5LJAC&pg=PA223&sig=PVA7Q1U_MyXinobyhOf54BwjShQ&hl=en#v=onepage&q&f=false Classical Mechanics] |
곡선의 시작점을 <math>(x_0,y_0)=(0,0)</math>, 끝점을 <math>(x_1,y_1)</math>라 두자. | 곡선의 시작점을 <math>(x_0,y_0)=(0,0)</math>, 끝점을 <math>(x_1,y_1)</math>라 두자. | ||
| 27번째 줄: | 18번째 줄: | ||
이제 곡선의 x좌표를 y의 함수로 생각하자. 곡선을 따라 내려올 때 걸리는 시간은 | 이제 곡선의 x좌표를 y의 함수로 생각하자. 곡선을 따라 내려올 때 걸리는 시간은 | ||
| − | + | :<math>T=\int \frac{1}{v} \, ds=\frac{1}{\sqrt{2g}}\int_{0}^{y} \frac{\sqrt{1+x'(y)^2}}{\sqrt{y}} \, dy</math> | |
| − | <math>T=\int \frac{1}{v} \, ds=\frac{1}{\sqrt{2g}}\int_{0}^{y} \frac{\sqrt{1+x'(y)^2}}{\sqrt{y}} \, dy</math> | ||
문제의 정의에 따라 이 적분값을 최소가 되게 하는 곡선을 찾아야 한다. | 문제의 정의에 따라 이 적분값을 최소가 되게 하는 곡선을 찾아야 한다. | ||
<math>F(y,x,x')=\frac{\sqrt{1+(x')^2}}{\sqrt{y}}</math> 에 대하여 [[오일러-라그랑지 방정식]] 을 적용하면, | <math>F(y,x,x')=\frac{\sqrt{1+(x')^2}}{\sqrt{y}}</math> 에 대하여 [[오일러-라그랑지 방정식]] 을 적용하면, | ||
| − | + | :<math>0 =\frac{\partial F}{\partial x} - \frac{d}{dy} \frac{\partial F}{\partial x'}=-\frac{d}{dy}(\frac{x'(y)}{\sqrt{y(1+x'(y)^2)}})</math> | |
| − | <math>0 =\frac{\partial F}{\partial x} - \frac{d}{dy} \frac{\partial F}{\partial x'}=-\frac{d}{dy}(\frac{x'(y)}{\sqrt{y(1+x'(y)^2)}})</math> | ||
적당한 상수 a에 대하여 <math>\frac{x'(y)}{\sqrt{y(1+x'(y)^2)}}=\frac{1}{\sqrt{2a}}</math>라 두자. | 적당한 상수 a에 대하여 <math>\frac{x'(y)}{\sqrt{y(1+x'(y)^2)}}=\frac{1}{\sqrt{2a}}</math>라 두자. | ||
| 41번째 줄: | 30번째 줄: | ||
(미분방정식의 여러 해에 대한 논의는 http://whistleralley.com/brachistochrone/brachistochrone.htm) | (미분방정식의 여러 해에 대한 논의는 http://whistleralley.com/brachistochrone/brachistochrone.htm) | ||
| − | + | : <math>x=\int_{0}^{y}\sqrt{\frac{y}{2a-y}}dy</math> | |
| − | <math>x=\int_{0}^{y}\sqrt{\frac{y}{2a-y}}dy</math> | ||
<math>y=2a\sin^2\frac{\theta}{2}=a(1-\cos\theta)</math>로 치환하면, <math>x=a(\theta-\sin\theta)</math>를 얻는다. | <math>y=2a\sin^2\frac{\theta}{2}=a(1-\cos\theta)</math>로 치환하면, <math>x=a(\theta-\sin\theta)</math>를 얻는다. | ||
| 51번째 줄: | 39번째 줄: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| 70번째 줄: | 45번째 줄: | ||
* http://en.wikipedia.org/wiki/Half-pipe ? | * http://en.wikipedia.org/wiki/Half-pipe ? | ||
* Half-Pipe Skateboarding ? | * Half-Pipe Skateboarding ? | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| 108번째 줄: | 58번째 줄: | ||
==수학용어번역== | ==수학용어번역== | ||
| − | * Brachistochrone curve | + | * Brachistochrone curve |
** brachistos - the shortest, chronos - time | ** brachistos - the shortest, chronos - time | ||
** 최단시간강하 곡선, 최속강하선, 최단강하선 | ** 최단시간강하 곡선, 최속강하선, 최단강하선 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| 139번째 줄: | 81번째 줄: | ||
* [http://www.jstor.org/stable/2974953 Exploring the Brachistochrone Problem]<br> | * [http://www.jstor.org/stable/2974953 Exploring the Brachistochrone Problem]<br> | ||
** LaDawn Haws, Terry Kiser, The American Mathematical Monthly, Vol. 102, No. 4 (Apr., 1995), pp. 328-336 | ** LaDawn Haws, Terry Kiser, The American Mathematical Monthly, Vol. 102, No. 4 (Apr., 1995), pp. 328-336 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| 150번째 줄: | 88번째 줄: | ||
* http://books.google.com/books?id=dptKVr-5LJAC&pg=PA223&sig=PVA7Q1U_MyXinobyhOf54BwjShQ&hl=en#v=onepage&q&f=false | * http://books.google.com/books?id=dptKVr-5LJAC&pg=PA223&sig=PVA7Q1U_MyXinobyhOf54BwjShQ&hl=en#v=onepage&q&f=false | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==링크== | ==링크== | ||
| − | |||
* [http://curvebank.calstatela.edu/brach/brach.htm The Brachistochrone] | * [http://curvebank.calstatela.edu/brach/brach.htm The Brachistochrone] | ||
[[분류:곡선]] | [[분류:곡선]] | ||
2014년 6월 16일 (월) 04:30 판
개요
- 중력을 받고 있는 물체가 정지상태에서 출발하여 가장 짧은 시간내에 하강하기 위해서 따라야 하는 곡선
- 1697년에 베르누이에 의하여 답이 출판
곡선의 시작점을 \((x_0,y_0)=(0,0)\), 끝점을 \((x_1,y_1)\)라 두자.
곡선을 따라 내려올때 걸리는 시간은 다음과 같이 구할 수 있다.
\(t=\int \frac{1}{v} \, ds\)(v는 속력, ds 는 길이요소, t는 시간)
에너지 보존 법칙 \(mgy=\frac{1}{2}mv^2\) 에서\(v=\sqrt{2gy}\).
이제 곡선의 x좌표를 y의 함수로 생각하자. 곡선을 따라 내려올 때 걸리는 시간은 \[T=\int \frac{1}{v} \, ds=\frac{1}{\sqrt{2g}}\int_{0}^{y} \frac{\sqrt{1+x'(y)^2}}{\sqrt{y}} \, dy\]
문제의 정의에 따라 이 적분값을 최소가 되게 하는 곡선을 찾아야 한다.
\(F(y,x,x')=\frac{\sqrt{1+(x')^2}}{\sqrt{y}}\) 에 대하여 오일러-라그랑지 방정식 을 적용하면, \[0 =\frac{\partial F}{\partial x} - \frac{d}{dy} \frac{\partial F}{\partial x'}=-\frac{d}{dy}(\frac{x'(y)}{\sqrt{y(1+x'(y)^2)}})\]
적당한 상수 a에 대하여 \(\frac{x'(y)}{\sqrt{y(1+x'(y)^2)}}=\frac{1}{\sqrt{2a}}\)라 두자.
이를 풀면 미분방정식 \(\frac{dx}{dy}=\sqrt{{\frac{y}{2a-y}}\) 를 얻는다.
(미분방정식의 여러 해에 대한 논의는 http://whistleralley.com/brachistochrone/brachistochrone.htm)
- \(x=\int_{0}^{y}\sqrt{\frac{y}{2a-y}}dy\)
\(y=2a\sin^2\frac{\theta}{2}=a(1-\cos\theta)\)로 치환하면, \(x=a(\theta-\sin\theta)\)를 얻는다.
여기서 상수 a는 주어진 점 \((x_1,y_1)\)를 지날 수 있는 값으로 결정된다.
따라서 사이클로이드를 얻었다.■
재미있는 사실
- http://en.wikipedia.org/wiki/Half-pipe ?
- Half-Pipe Skateboarding ?
관련된 항목들
수학용어번역
- Brachistochrone curve
- brachistos - the shortest, chronos - time
- 최단시간강하 곡선, 최속강하선, 최단강하선
사전 형태의 자료
- http://ko.wikipedia.org/wiki/
- http://en.wikipedia.org/wiki/Brachistochrone_problem
- http://curvebank.calstatela.edu/brach/brach.htm
- http://mathworld.wolfram.com/BrachistochroneProblem.html
관련논문
- The Brachistochrone Problem
- Nils P. Johnson, The College Mathematics Journal, Vol. 35, No. 3 (May, 2004), pp. 192-197
- Exploring the Brachistochrone Problem
- LaDawn Haws, Terry Kiser, The American Mathematical Monthly, Vol. 102, No. 4 (Apr., 1995), pp. 328-336
관련도서