프로듀스 X 101 투표 조작 논란

개요

• 프로듀스 101 X 투표 조작 논란이 있다.
• 조작 주장의 근거는 득표수와 관련된 우연으로 보기 힘든 여러 현상들이다.
• 여러 번의 투표 결과를 득표수 그대로 더하지 않고, 적당히 가중치를 주어 합산하는 과정이 있었다면, 위에서 발견된 현상들은 대체로 설명이 가능하다.
• 가령 네 번의 투표가 있었고, 각 투표가 예를 들어 모두 25%만큼 기여하도록 해야 한다면, 득표결과에 적당한 수를 곱하고 반올림하는 과정을 거쳤을 수도 있다.
  • 이 과정이 문제를 일으킬 가능성에 대해서는 프로듀스 X 101 투표 조작 논란 : 7494.442라는 수 항목을 참조
• 7월 24일 엠넷이 내놓은 "득표수로 순위를 집계한 뒤 득표율로 계산해 소수점 둘째 자리로 반올림하고 이를 다시 득표수로 환산했다"는 해명은 따라서 납득할만하다.
• 엠넷이 이번 사태로 배워야 할 핵심 교훈 : 계산 중간에 숫자들을 반올림하고 계산을 계속 수행하면 문제가 될 수 있다. 필요하다면 반올림은 모든 계산을 한 다음, 마지막 한번만.
• 단, 이 글은 방송과 관련된 어떤 조작도 없었음을 증명하지는 않는다

설명

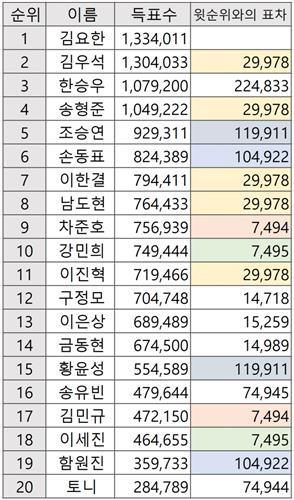
프듀 101 X 득표 테이블

이 글 https://gall.dcinside.com/board/view/?id=producex&no=2998354 에서 지적되었듯이, 프듀의 득표 테이블은 $\alpha=7494.442$에 적당한 자연수 $n$를 곱한 다음 반올림하여 얻어진 것과 12위 딱 한 곳만 제외하고 모두 같다. 12위의 표는 오타로 보는 것이 맞을 것이다.

득표수를 집계하는데 이런 다소 이상한 작업이 실행된 가능한 시나리오는 이러하다.

1. 어떤 이유에선지 집계를 담당한 누군가는 1위부터 20위까지의 득표수가 모두 정수인 동시에 합계가 2000이 되도록 만든다.
2. 최종투표 이전에도 여러 번의 투표가 있었고, 또 서로 다른 종류의 투표 방식도 있었을 수 있다. 여러 투표 사이의 공정한 비교를 위해 각각의 투표가 모두 합이 2000이 되도록 만드는 것과 같은 작업들이 필요했을 가능성이 있다. (정규화 과정)
3. 그렇게 해서 얻어진 숫자가 1위 178, 2위 174, ..., 20위 38이다.
4. 이 숫자들을 다시 득표수처럼 보이도록 적당한 숫자 ($\alpha=7494.442$)를 곱한 다음 반올림을 했고, 이 숫자들이 방송에 노출되었다.

이렇게 몇 단계를 거치면서 약간 변화된 득표수는 크기의 순서를 달리하지는 않지만, 이제 재미있는 수학적 현상을 보이는 수들로 거듭나게 된다. 그리고 그것이 수많은 조작 논란을 가져오게 된 원인으로 보인다. 그렇다면 재미있는 수학적 현상이란 무엇인가? 모든 득표수가 7494와 7495의 배수의 합으로 나타난다는 것이다. 아래 표의 오른쪽에서 이를 정리했다.

\begin{array}{c|cc|c} \text{} & \text{n} & \text{round} (n \alpha ) & \text{} \\ \hline 1 & 178 & 1334011 & 99\times7494+79\times7495 \\ 2 & 174 & 1304033 & 97\times7494+77\times7495 \\ 3 & 144 & 1079200 & 80\times7494+64\times7495 \\ 4 & 140 & 1049222 & 78\times7494+62\times7495 \\ 5 & 124 & 929311 & 69\times7494+55\times7495 \\ 6 & 110 & 824389 & 61\times7494+49\times7495 \\ 7 & 106 & 794411 & 59\times7494+47\times7495 \\ 8 & 102 & 764433 & 57\times7494+45\times7495 \\ 9 & 101 & 756939 & 56\times7494+45\times7495 \\ 10 & 100 & 749444 & 56\times7494+44\times7495 \\ 11 & 96 & 719466 & 54\times7494+42\times7495 \\ 12 & 94 & 704478 & 52\times7494+42\times7495 \\ 13 & 92 & 689489 & 51\times7494+41\times7495 \\ 14 & 90 & 674500 & 50\times7494+40\times7495 \\ 15 & 74 & 554589 & 41\times7494+33\times7495 \\ 16 & 64 & 479644 & 36\times7494+28\times7495 \\ 17 & 63 & 472150 & 35\times7494+28\times7495 \\ 18 & 62 & 464655 & 35\times7494+27\times7495 \\ 19 & 48 & 359733 & 27\times7494+21\times7495 \\ 20 & 38 & 284789 & 21\times7494+17\times7495 \\ \end{array}

애초에 득표수 그대로를 발표했으면, 아무 논란이 없었을 것이다. 세어서 얻어진 득표수가 아니라 위의 과정을 거쳐 얻어진 숫자를 공개한 것은 조작이라기보다는 미숙한 처리라고 보는 것이 더 적절할 것이다. 숫자들이 달라질 수 있다는 걸 이해하지 못했거나, 아니면 방송에 내보내야 할 것이 뒤바뀐 단순 실수가 일어난 것이다. (삐딱하게 보면 투표참여자수를 부풀리려는 악의가 있었을 가능성도 배제할 수는 없다)

그렇다면 이제 왜 이와 같은 수학적 현상이 나타나는지를 설명하려 한다.

의도치 않은 수학적 결과들

득표수와 관련된 많은 의혹을 설명할 수 있는 하나의 수학적 명제가 있다.

정리

실수 $\alpha>0$가 주어져 있고, $\alpha$의 정수부분을 $f$라 하자. 임의의 자연수 $n$에 대하여, $n\alpha$를 반올림해서 얻어지는 정수는 $f$와 $(f+1)$의 음이 아닌 배수의 합으로 표현된다.

(증명)

최대정수함수 $[\cdot]$를 사용하자.

실수 $\beta=\alpha-f$에 대하여, 부등식 $0\leq \beta<1$이 성립한다. 이제 두 정수 $x,\,y$를 다음과 같이 정의하자 : $$y=[n\beta],\qquad x=n-y.$$

부등식 $0\leq n\beta<n$에 의해 $0\leq y=[n\beta]\leq n-1$이고, 따라서 $x\geq 1$이다.

이제 $[n\alpha]$를 $A$라 두자. 그러면 $n\alpha$를 반올림해서 얻어지는 정수는 $A$이거나 $A+1$이 된다. 따라서 $A$와 $A+1$ 모두 $f$와 $(f+1)$의 음이 아닌 배수의 합으로 표현됨을 보이는 것으로 충분하다.

먼저, $$ \begin{align} A & = [n\alpha] =[n(f+\beta)] \\ & = nf+[n\beta] = (x+y)f+y \\ & =xf+y(f+1) \end{align} $$ 이 성립한다. 따라서, $$ \begin{align} A+1 & = xf+y(f+1)+1\\ & =(x-1)f+(y+1)(f+1). \end{align} $$

■

건조하게 적었지만, 이는 흥미로운 점이 있는 수론적 현상이라 할 수 있으며, 이번 논란이 촉발시킨 발견이다. 이 현상이 왜 흥미로운 것인지는 프로베니우스 디오판투스 방정식과 동전 바꾸기 문제 (coin exchange problem)에 대해 생각할 때 더 깊게 이해할 수 있다.

간단한 예를 보자.

예

• $\alpha=5.2$, 정수부분은 $f=5$
• 예를 들어, $n=3$이라면 $n\alpha=15.6$

이제 $n\alpha=15.6$을 반올림하면 $m=16$이고, $16 = 2\times 5 + 1 \times 6$

더 현실적인 예를 생각해 보자.

예

• $\alpha=7494.442$, 정수부분은 $f=7494$

다음과 같은 선택을 해보자.

• $n=178$

그러면 $n\alpha=1334010.676$를 반올림하여, $m=1334011$이고 $m=1334011 = 99 \times 7494 + 79 \times 7495$

또 다른 예를 들자면,

• $n=102$

그러면 $n\alpha=764433.084$를 반올림하여, $m=764433$이고 $m=764433 = 57 \times 7494 + 45 \times 7495$

이제부터는 이를 바탕으로 득표수와 관련된 여러 의혹을 설명한다.

토니의 득표수와 관련된 미스테리

20위 토니와 18위의 득표수의 합은 $284789 + 464655=749444$로 10위의 득표수와 같다. 일반적으로 7494와 7495의 배수의 합으로 표현되는 두 수의 합도 역시 7494와 7495의 배수의 합으로 표현가능하다. 대수적으로 표현하면 다음과 같다 :

$$ (7494a+7495b)+(7494c+7495d) = 7494(a+c)+7495(b+d). $$

따라서 둘의 득표수를 더해서 다른 사람의 득표와 같아지는 것은 일어날 수 있는 일이 일어난 것이다. 꼭 20등 토니가 아니더라도 6등과 16등의 표를 더해 2등의 표가 나오는 일도 발생했다.

아래의 표는 a등의 표와 b등의 표를 더했을 때, c등의 표가 나온 경우를 모두 나열한 것이다.

\begin{array}{cc|c} a & b & c \\ \hline 4 & 20 & 1 \\ 6 & 16 & 2 \\ 7 & 20 & 3 \\ 8 & 20 & 4 \\ 10 & 15 & 2 \\ 13 & 19 & 4 \\ 16 & 20 & 8 \\ 17 & 20 & 9 \\ 18 & 20 & 10 \\ 19 & 19 & 11 \\ \end{array}

윗순위와의 표차

1위와 2위의 표차이는 29978이다. 이 수는 7494와 7495의 배수의 합으로 표현되는 두 수의 차이이므로, 역시 7494와 7495의 배수의 합으로 표현가능하다. 대수적으로 표현하면 다음과 같다 :

$$ (7494a+7495b)-(7494c+7495d) = 7494(a-c)+7495(b-d). $$

표는 다음과 같다. \begin{array}{c|c|c} 1-2 & 29978 & 2\times7494+2\times7495 \\ 2-3 & 224833 & 17\times7494+13\times7495 \\ 3-4 & 29978 & 2\times7494+2\times7495 \\ 4-5 & 119911 & 9\times7494+7\times7495 \\ 5-6 & 104922 & 8\times7494+6\times7495 \\ 6-7 & 29978 & 2\times7494+2\times7495 \\ 7-8 & 29978 & 2\times7494+2\times7495 \\ 8-9 & 7494 & 1\times7494+0\times7495 \\ 9-10 & 7495 & 0\times7494+1\times7495 \\ 10-11 & 29978 & 2\times7494+2\times7495 \\ 11-12 & 14988 & 2\times7494+0\times7495 \\ 12-13 & 14989 & 1\times7494+1\times7495 \\ 13-14 & 14989 & 1\times7494+1\times7495 \\ 14-15 & 119911 & 9\times7494+7\times7495 \\ 15-16 & 74945 & 5\times7494+5\times7495 \\ 16-17 & 7494 & 1\times7494+0\times7495 \\ 17-18 & 7495 & 0\times7494+1\times7495 \\ 18-19 & 104922 & 8\times7494+6\times7495 \\ 19-20 & 74944 & 6\times7494+4\times7495 \\ \end{array}

따라서 이 현상도 역시 일어날 수 있는 일이 일어난 것이다.

결론

1위부터 20위까지의 득표수의 합이 2000이 되도록 만드는 과정에서 한번의 반올림이 필요했다. 여기에 다시 적당한 수를 곱한 다음 반올림을 했다. 득표수의 조작처럼 보이는 수학적 현상들은 이러한 간단한 계산 과정의 의도치 않은 결과로 이해할 수 있다.

관련된 항목들

• 프로베니우스 디오판투스 방정식과 동전 바꾸기 문제 (coin exchange problem)
• 2012년 대선 개표와 로지스틱 곡선