Lectures on dilogarithm function

overview

• volumes of hyperbolic 3-manifolds
• special values of Dedekind zeta functions

introdcution

• definition of dilogarithm function
• analytic continuation
• Bloch-Wigner dilogarithm function
• functional equations
• hyperbolic volumes
• values of the Dedekind zeta function at s=2

• 다이로그 함수는 복소수 \(|z|<1\)에 대하여 다음과 같이 정의됨\[\operatorname{Li}_ 2(z)= \sum_{n=1}^\infty {z^n \over n^2}\]\[|z|\leq 1\] 에서 고르게 수렴하는 급수이므로, \(|z|\leq 1\)에서 연속
• 다음과 같은 적분으로 정의하면 해석적으로 확장가능\[\operatorname{Li}_ 2(z) = -\int_0^z{{\ln (1-t)}\over t} dt \] for \(z\in \mathbb C-[1,\infty)\)

special values

\(\mbox{Li}_{2}(0)=0\)

\(\mbox{Li}_{2}(1)=\frac{\pi^2}{6}\)

\(\mbox{Li}_{2}(-1)=-\frac{\pi^2}{12}\)

\(\mbox{Li}_{2}(\frac{1}{2})=\frac{\pi^2}{12}-\frac{1}{2}\log^2(2)\)

\(\mbox{Li}_{2}(\frac{3-\sqrt{5}}{2})=\frac{\pi^2}{15}-\log^2(\frac{1+\sqrt{5}}{2})\)

\(\mbox{Li}_{2}(\frac{-1+\sqrt{5}}{2})=\frac{\pi^2}{10}-\log^2(\frac{1+\sqrt{5}}{2})\)

\(\mbox{Li}_{2}(\frac{1-\sqrt{5}}{2})=-\frac{\pi^2}{15}+\frac{1}{2}\log^2(\frac{1+\sqrt{5}}{2})\)

\(\mbox{Li}_{2}(\frac{-1-\sqrt{5}}{2})=-\frac{\pi^2}{10}+\frac{1}{2}\log^2(\frac{1+\sqrt{5}}{2})\)

functional equations

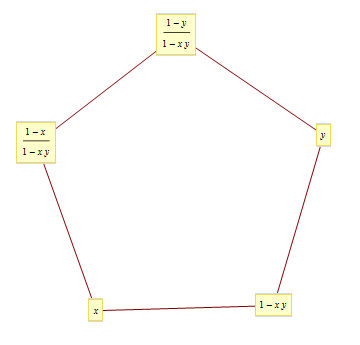
• 5항 관계식은 다이로그 함수의 가장 중요한 항등식의 하나이다.\[\mbox{Li}_ 2(x)+\mbox{Li}_ 2(y)+\mbox{Li}_ 2 \left( \frac{1-x}{1-xy} \right)+\mbox{Li}_ 2(1-xy)+\mbox{Li}_ 2 \left( \frac{1-y}{1-xy} \right)=\frac{\pi^2}{2}-\log(x)\log(1-x)-\log(y)\log(1-y)+\log (\frac{1-x}{1-xy})\log (\frac{1-y}{1-xy})\]

5항 관계식

• 로저스 다이로그 함수 \(L(x)\)
• \(0\leq x,y\leq 1\) 일 때, 다음이 성립한다

\[L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)=\frac{\pi^2}{2}\]

• \(1-x_{i}=x_{i-1}x_{i+1}\), \(x_0=x\), \(x_2=y\)로 정의되는 점화식은 주기가 5인 수열이 된다\[x_0=x, x_1=1-xy, x_2=y, x_3=\frac{1-y}{1-xy}, x_4=\frac{1-x}{1-xy}\]
• 집합 \(\{0,1,\infty,y,xy\}\) 에서 4개의 원소를 뽑아 얻어지는 교차비(cross ratio)

Rogers dilogarithm

• \(x\in (0,1)\)에서 로저스 다이로그 함수를 다음과 같이 정의

\[L(x)=\operatorname{Li}_ 2(x)+\frac{1}{2}\log x\log (1-x)=-\frac{1}{2}\int_{0}^{x}\left(\frac{\log(1-y)}{y}+\frac{\log(y)}{1-y}\right)dy\]

• \((-\infty,0],[1,+\infty)\)를 제외한 복소평면으로 해석적확장됨
• \(dL(y)=\frac{1}{2}[\log(y)d\log (1-y)-\log(1-y)d\log (y)]\)

algebraic K-theory

• $F$ : number field
• $K_0(F) = \mathbb{Z}$
• $K_1(F) = F^{\times}$
• $K_2(F) = F^{\times}\otimes F^{\times}/\langle x\otimes (1-x) \rangle$
• $K_0(\mathcal{O}_F) = \mathbb{Z}\oplus Cl_F$
• $K_1(\mathcal{O}_F) = (\mathcal{O}_F)^{\times}$
• $K_2(\mathcal{O}_F)$ : finite group

Borel's regulator

• Let $F$ be a number field with $[F:\mathbb{Q}]=r_1+2r_2$
• Borel constructed a map

$$ K_{2i-1}(F) \to \mathbb{R}^{d_{i}} $$ where $d_i = r_2$ or $r_1+r_2$ depending on the parity of $i$

• this can be used to show
  • $\operatorname{rank} K_3 =r_2$
  • $\operatorname{rank} K_5=r_1+r_2$
  • $\operatorname{rank} K_7=r_2$
• let $\mathcal{O}_{F}$ be the ring of integers of $F$
• for any field L of characteristic zero, $K_{i}(\mathcal{O}_{F})\otimes_{\Z}L$ is naturally isomorphic to $K_{i}(F)\otimes_{\Z}L$ for $i>1$
• http://www.ams.org/mathscinet-getitem?mr=1354171
• https://books.google.nl/books?id=ru7BywKC1d4C&pg=PA475&lpg=PA475&dq=Values+of+zeta-functions+at+integers,+cohomology+and+polylogarithms&source=bl&ots=BznObLSgR-&sig=X9LeM98z4cxje_axpCZjeUaY66U&hl=en&sa=X&ei=5rCMU-bqNMLwPInpgLgH&redir_esc=y#v=onepage&q=Values%20of%20zeta-functions%20at%20integers%2C%20cohomology%20and%20polylogarithms&f=false

Bloch-Wigner dilogarithm

• Let us define a variant of the dilogarithm function : the Bloch-Wigner dilogarithm function. It is given by

$$D(z)=\text{Im}(\operatorname{Li}_2(z))+\log|z|\arg(1-z).$$

• It is a real analytic function on $\mathbb{C}$ except at 0 and 1, where it is continuous but not differentiable.
• Since $D(\bar{z})=-D(z)$, it vanishes on $\mathbb{R}$.
• It satisfies the following functional equations :

\begin{equation}\label{functid1} D(x)+D(1-xy)+D(y)+D(\frac{1-y}{1-xy})+D(\frac{1-x}{1-xy})=0, \end{equation} \begin{equation}\label{functid2} D(x)+D(1-x) =D(x)+D(\frac{1}{x})=0. \end{equation}

regulator in algebraic K-theory

• The Bloch-Wigner dilogarithm $D(z)$ can be used to define a map from $\mathcal{B}(\mathbb{C})$ to $\mathbb{R}$.
• For $\xi=\sum_{i} n_i[x_i] \in \mathcal{B}(\mathbb{C})$, let $D(\xi)=\sum_{i} n_i D(x_i)$.
• By (\ref{functid1}) and (\ref{functid2}), it is well-defined.
• Let $F$ be a number field of degree $r_1+2r_2$ over $\mathbb{Q}$ where $r_1$ denotes the number of real embeddings and $r_2$ the number of complex non-real embeddings up to conjugation.
• For an embedding $\sigma : F\hookrightarrow \mathbb{C}$ and $\xi \in \mathcal{B}(F)$, we may consider $D\left(\sigma(\xi)\right)$.
• If $D\left(\sigma(\xi)\right)=0$ for all such embeddings $\sigma$, then $\xi \in \mathcal{B}(F)$ is a torsion element in $\mathcal{B}(F)$.

Dedekind zeta

• 데데킨트 제타함수에 대해서 다음과 같은 함수방정식이 성립

\[\xi_{K}(s)=\left|d_K\right|{}^{s/2} 2^{r_2 (1-s)} \pi ^{\frac{1}{2} \left(-r_1-2 r_2\right) s}\Gamma \left(\frac{s}{2}\right)^{r_1} \Gamma (s)^{r_2}\zeta _K(s)\]\[\xi_{K}(s) = \xi_{K}(1 - s)\]

• at $s=-n, n=1,2\cdots$, $\zeta_K(s)$ has zero of order $r_2$ or $r_1+r_2$ if $n$ is even or odd, respectively

$$ 2^{(m+1) r_2} \pi^{-\frac{1}{2} m \left(-r_1-2 r_2\right)} \left(\zeta_K(-m) \right) (\Gamma (-m))^{r_2} \left(\frac{1}{2} \Gamma (-m)\right)^{r_1} \left| d_K\right| {}^{-\frac{m}{2}}\\ =2^{-m r_2} \pi ^{\frac{1}{2} (m+1) \left(-r_1-2 r_2\right)} \left(\zeta _K(m+1) \right) \left(\frac{1}{2} \Gamma (m+1)\right)^{r_1} (\Gamma (m+1))^{r_2} \left| d_K\right| {}^{\frac{m+1}{2}} $$

디리클레 유수 공식

• \(s=1\) 에서의 유수(residue)는 디리클레 유수 (class number) 공식으로 주어진다

\[ \lim_{s\to 1} (s-1)\zeta_K(s)=\frac{2^{r_1}\cdot(2\pi)^{r_2}\cdot h_K\cdot R_K}{w_K \cdot \sqrt{|d_K|}}\]

• \(s=0\) 에서 order 가 \(r_1+r_2-1\) 인 zero를 가지며 다음이 성립한다\[ \lim_{s\to 0}\frac{\zeta_K(s)}{s^{r_1+r_2-1}}=-\frac{h_K R_K}{w_K}\]

Zagier, Bloch, Suslin

• \([K : \mathbb{Q}] = r_1 + 2r_2\)일 때,

\[ \frac{\pi^{r_2}}{|d_{K}|}\lim_{s\to -1} \frac{\zeta_{K}(s)}{(s+1)^{r_2}} = (-1)^{r_1+r_2}2^{-r_1-3r_2}\frac{|d_{K}|^{1/2}}{\pi^{2(r_1 + r_2)}} \zeta_{K}(2) \sim_{\mathbb{Q^{\times}}} \det\left(D(\sigma_i(\xi_j))\right)_{1\leq i,j\leq r_2} \] 여기서 \(\xi_i,(i=1,\cdots, r_2)\) 는 Bloch group \(B(K)\otimes \mathbb{Q}\)의 $\mathbb{Q}$-basis D는 블로흐-비그너 다이로그(Bloch-Wigner dilogarithm) 함수이며, \(a\sim_{\mathbb{Q^{\times}}} b\) 는 \(a/b\in\mathbb{Q}\) 를 의미함

background

• 다른게 아니라 저랑 강원대 강순이 박사님이랑 최근에 Zagier 교수님 쓰신 dilogarithm 논문에 관심이 생겼는데 quantum dilogarithm을 포함해서 자기에 교수님 논문 내용을 강연해줄 수 있는지 부탁드리고자 편지드려요.
• Bloc 그룹도 강의해줄 수 있으면 더 좋지만, 아니면 남 추측 관련해서 공부했던 내용이라도 강의해주면 많은 도움이 될 것 같아요.
• 자기에 교수님 dilogarithm 논문을 읽는데, 부끄럽지만 무슨 말인지 전혀 모르겠더라고요.
• q가 나오는 부분과 점근식 부분은 그래도 알겠는데, 나머지 부분들은 능력 밖이라 도움 받을 수 있나해서 여쭤본 겁니다.
• 그러니까 Bloc 그룹도 이 논문에 나오는 정도 이해할 수 있으면 저는 만족이에요.
• quantum dilogarithm 쪽으로 무언가 더 해볼 여지가 있는지 궁금해서 우선 자기에 교수님 논문부터 시작해보려고 했었는데, 시작부터 어렵네요

related items

• K-theory of number fields and Borel's regulator

links

• 틀:수학노트
• 틀:수학노트
• 틀:수학노트
• 틀:수학노트