"사다리타기의 수학"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
수학용어번역==
Pythagoras0 (토론 | 기여) 잔글 (찾아 바꾸기 – “<h5>” 문자열을 “==” 문자열로) |
Pythagoras0 (토론 | 기여) 잔글 (찾아 바꾸기 – “</h5>” 문자열을 “==” 문자열로) |
||
| 46번째 줄: | 46번째 줄: | ||
| − | ==관련된 항목들 | + | ==관련된 항목들== |
* [[대칭군 (symmetric group)]] | * [[대칭군 (symmetric group)]] | ||
| 54번째 줄: | 54번째 줄: | ||
| − | ==매스매티카 파일 및 계산 리소스 | + | ==매스매티카 파일 및 계산 리소스== |
* https://docs.google.com/leaf?id=0B8XXo8Tve1cxYWIwYzI5MDctZmE1OC00MmQwLWI3MjEtZmIyMzBhN2VlNjBm&sort=name&layout=list&num=50 | * https://docs.google.com/leaf?id=0B8XXo8Tve1cxYWIwYzI5MDctZmE1OC00MmQwLWI3MjEtZmIyMzBhN2VlNjBm&sort=name&layout=list&num=50 | ||
| 69번째 줄: | 69번째 줄: | ||
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">수학용어번역 | + | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">수학용어번역== |
* 단어사전<br> | * 단어사전<br> | ||
| 87번째 줄: | 87번째 줄: | ||
| − | ==사전 형태의 자료 | + | ==사전 형태의 자료== |
* [http://ko.wikipedia.org/wiki/%EC%82%AC%EB%8B%A4%EB%A6%AC%ED%83%80%EA%B8%B0 http://ko.wikipedia.org/wiki/사다리타기] | * [http://ko.wikipedia.org/wiki/%EC%82%AC%EB%8B%A4%EB%A6%AC%ED%83%80%EA%B8%B0 http://ko.wikipedia.org/wiki/사다리타기] | ||
| 100번째 줄: | 100번째 줄: | ||
| − | ==리뷰논문, 에세이, 강의노트 | + | ==리뷰논문, 에세이, 강의노트== |
| 108번째 줄: | 108번째 줄: | ||
| − | ==관련논문 | + | ==관련논문== |
* http://www.jstor.org/action/doBasicSearch?Query= | * http://www.jstor.org/action/doBasicSearch?Query= | ||
| 118번째 줄: | 118번째 줄: | ||
| − | ==관련도서 | + | ==관련도서== |
* 도서내검색<br> | * 도서내검색<br> | ||
** http://books.google.com/books?q= | ** http://books.google.com/books?q= | ||
** http://book.daum.net/search/contentSearch.do?query= | ** http://book.daum.net/search/contentSearch.do?query= | ||
2012년 11월 1일 (목) 12:50 판
개요
- 제비뽑기에 사용되는 도구
- 수학적으로 각각의 사다리는 대칭군 (symmetric group) 의 원소와 일대일대응된다
대칭군과의 관계
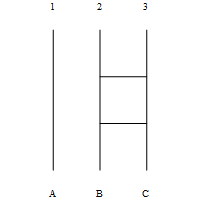
- 세 사람이 등장하는 사다리의 경우
- 다음 두 사다리는, 아무 것도 없는 경우와 같다
- 다음 두 사다리는 같은 결과를 준다
- 위의 사실들은 대칭군 (symmetric group) 의 생성원들 사이에 성립하는 다음 관계와 대응된다 (\(\sigma_i=(i, i+1)\) 라 하자)
- \({\sigma_i}^2 = 1\)
- \(\sigma_i\sigma_{i+1}\sigma_i = \sigma_{i+1}\sigma_i\sigma_{i+1}\) (또는 \((\sigma_i\sigma_{i+1})^3=1\) 로 쓸 수 있다)
역사
메모
- Ladders, Codes, and Actions
- http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=2684
- http://blog.naver.com/PostView.nhn?blogId=artkishan&logNo=140000659705
- http://www2.edc.org/makingmath/studentWork/amidaKuji/AmidaKujiByDavidSenft.pdf
- Math Overflow http://mathoverflow.net/search?q=
관련된 항목들
매스매티카 파일 및 계산 리소스
- https://docs.google.com/leaf?id=0B8XXo8Tve1cxYWIwYzI5MDctZmE1OC00MmQwLWI3MjEtZmIyMzBhN2VlNjBm&sort=name&layout=list&num=50
- http://www.wolframalpha.com/input/?i=
- http://functions.wolfram.com/
- NIST Digital Library of Mathematical Functions
- Abramowitz and Stegun Handbook of mathematical functions
- The On-Line Encyclopedia of Integer Sequences
- Numbers, constants and computation
- 매스매티카 파일 목록