"매듭이론 (knot theory)"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
잔글 (찾아 바꾸기 – “<br><math>” 문자열을 “:<math>” 문자열로)
잔글 (찾아 바꾸기 – “수학사연표” 문자열을 “수학사 연표” 문자열로)
138번째 줄: 138번째 줄:
 
* 1990년 존스, 위튼 필즈메달 수상
 
* 1990년 존스, 위튼 필즈메달 수상
 
* http://www.google.com/search?hl=en&tbs=tl:1&q=knot+theory
 
* http://www.google.com/search?hl=en&tbs=tl:1&q=knot+theory
−
* [[수학사연표 (역사)|수학사연표]]
+
* [[수학사 연표]]
 
*   
 
*   
  

2013년 1월 14일 (월) 15:31 판

개요

  • 매듭(knot)
    • 3차원 상에 놓인 원과 위상동형인 곡선, 또는 3차원 상에 놓인 자기자신과 만나지 않는 닫힌 곡선
  • 고리(link)
  • 동위(isotopy)
    • 3차원 상에서 매듭을 끊지 않는 연속적인 변형
  • 매듭 diagram
  • 라이데마이스터 변형
  • 20세기말에 통계역학, 양자군, 양자장론과의 관계가 발견되어 큰 발전

중요한 문제

  • 주어진 두 매듭이 동위관계에 있는지를 판단하는 문제
  • 매듭의 분류
  • 중요 미해결 문제
    • Does there exist a knot in R3, different from the unknot , whose Jones polynomial is equal to 1?”

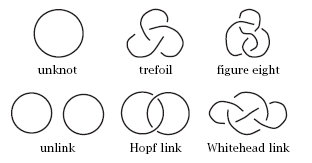
매듭과 고리의 예



매듭 diagram

  • 3차원 공간에 놓인 매듭을 2차원 평면에 사영하여 얻어짐



라이데마이스터 변형

  • 매듭 diagram 에 가하는 변형
  • 매듭이 3차원 공간에서의 연속적인 변형을 통하여 다른 매듭으로 변하면, 매듭 diagram에 세가지 라이데마이스터 변형을 가하여 같은 결과를 얻을 수 있다
  • 매듭으로부터 정의된 양이 불변량임을 증명하는데 흔히 사용
  • 라이데마이스터 변형 1 - disapperanace of a little loop
  • 라이데마이스터 변형 2 - twin crossing 의 제거
  • 라이데마이스터 변형 3 - 크로싱 위로 thread의 이동


라이데마이스터 변형 I 라이데마이스터 변형 II 라이데마이스터 변형 III




불변량

  • 동위관계에 있는 다항식에 대해서는 같은 값을 주는 양
  • 동의관계에 있는 매듭에는 같은 다항식이 대응되나, 다항식이 같다고 매듭이 동위관계에 있다고는 말할수 없다
  • 서로 다른 매듭을 구분할 수 있는 더 강력한 불변량을 찾는 것은 매듭이론의 중요한 주제이다
  • 알렉산더-콘웨이 다항식
  • HOMFLY 다항식
  • 존스 다항식
  • 바실리예프 다항식
  • 실타래 관계를 이용하여 정의되는 경우가 많다



실타래 관계 (skein relation)

  • 나머지 부분이 같고, 한 교차점에서만 다른 매듭의 oriented diagram을 실타래 diagram이라 한다
  • 유향매듭 L이 있을때, 다음과 같이 \(L_{+},L_{-},L_{0}\) 을 정의한다
  • 다항식으로 정의되는 여러 불변량들은 이 세 실타래들이 만족시키는 관계를 가지며, 이를 실타래 관계라 한다
  • 불변량을 재귀적으로 정의할 수 있게 된다

알렉산더-콘웨이 다항식

  • 각 매듭에 대해 정의되는 z를 변수로 가지는 정수계수다항식 \(\nabla(\cdot)\)
  • 실타래 관계(skein relation)\[\nabla(O) = 1\]\[\nabla(L_+) - \nabla(L_-) = z \nabla(L_0)\]



존스 다항식

  • 각 매듭에 대해 정의되는 \(t^{1/2}\)를 변수로 가지는 정수계수 로랑다항식 \(V(\cdot)\)
  • 실타래 관계(skein relation)\[V(O) = 1\]\[(t^{1/2} - t^{-1/2})V(L_0) = t^{-1}V(L_{+}) - tV(L_{-})\]




홈플라이(HOMFLY) 다항식

  • HOMFLY는 사람의 이름이 아니라, 발견자 여러 명의 머리글자이다
  • 알렉산더-콘웨이 다항식과 존스 다항식의 일반화
  • 매듭에 정의되는 이변수다항식 \(P(\cdot)\)
  • 실타래 관계



재미있는 사실



역사



메모

관련된 항목들

  • 양자군 (quantum group)


계산 리소스

수학용어번역



사전 형태의 자료



동영상 강연



관련논문과 소개글



관련도서



관련링크와 웹페이지



관련기사



블로그

원본 주소 "https://wiki.mathnt.net/index.php?title=매듭이론_(knot_theory)&oldid=25611"