Kissing number and sphere packings

개요

• Kissing number
  • 각 차원에서 주어진 구의 주변에 같은 크기의 구를 최대 몇 개까지 접하도록 배치할수 있는가의 문제
  • 1차원에서는 2, 2차원에서는 6, 3차원에서는 12, 4차원에서는 24

• • 8차원에서는 240, 24차원에서는 196560 임이 알려져 있음.
    • 이는 8차원의 E8, 24차원의 리치(Leech)격자에 의해 얻어짐.
  • 나머지 차원은 아직 미해결.
• Sphere packings
  • n차원 공간을 가장 효율적으로 채우는 구의 배치는 무엇인가의 문제
  • 일반적인 경우는 매우 어렵고, 좀더 접근이 가능한 경우인 격자 모양의 배치가 수학적으로 중요한 문제.

저차원에서의 결과

1차원

• kissing number = 2

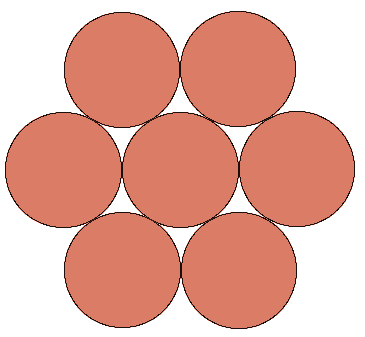
2차원

• kissing number = 6

3차원

• kissing number = 12
• 1694년 Isaac Newton 과 David Gregory가 이에 대해 토론함 ([ConwaySloane]).
• 1953년 Schütte와 van der Waerden에 의해 처음으로 제대로 증명됨 ([ConwaySloane])
• [Musin05]

4차원

• kissing number = 24
• 2003년 Oleg R. Musin에 의해 증명
• [Musin05],'[Musin2008]'

고차원

• 5차원 이상에서는 8,24 차원을 제외하고 미해결
• 8차원에서는 240, 24차원에서는 196560 임이 알려져 있음.
  • 이는 8차원의 E8, 24차원의 리치 격자(Leech lattice)에 의해 얻어짐.

메모

• 피타고라스의 창
  • E8이란 무엇인가 (1) : 들어가며
  • E8이란 무엇인가 (2) : 8차원에서 내려온 그림자
  • E8이란 무엇인가 (3) : 8차원의 눈꽃송이
  • E8이란 무엇인가 (번외편) - E8과 모뎀

역사

• 1694, Newton and Gregory discussed if the solution in dimension 3
• http://www.google.com/search?hl=en&tbs=tl:1&q=kissing+number
• 수학사 연표

관련된 학부 과목과 미리 알고 있으면 좋은 것들

• 이차형식
• 코딩이론

관련된 항목들

• Special functions
• Number 12 and 24
• E8

수학용어번역

• kissing - 대한수학회 수학용어집

사전 형태의 자료

• http://en.wikipedia.org/wiki/Sphere_packing
• http://en.wikipedia.org/wiki/Kissing_number_problem

리뷰, 에세이, 강의노트

• Lattices, Linear Codes and Invariants, Part I.
  • Noam D. Elkies., 1238. NOTICES OF THE AMS. VOLUME. 47, NUMBER. 10.
• Lattices, Linear Codes and Invariants,. Part II
  • Noam D. Elkies., 1382. NOTICES OF THE AMS. VOLUME. 47, NUMBER. 11.

관련논문

• High accuracy semidefinite programming bounds for kissing numbers
  • Hans D. Mittelmann, Frank Vallentin, 2009
• [Musin08]The kissing number in four dimensions
  • Oleg R. Musin, Annals of Mathematics, 168 (2008), No. 1, 1-32
• New upper bounds for kissing numbers from semidefinite programming
  • Christine Bachoc, Frank Vallentin, 2007
• [Musin05]An extension of Delsarte's method. The kissing problem in three and four dimensions
  • Oleg R. Musin, The Proceedings of COE Workshop on Sphere Packings (Nov. 1st - Nov. 5th, 2004), Kyushu University, Japan, 2005, 1-25
• Kissing numbers, sphere packings and some unexpected proofs
  • F. Pfender, G.M. Ziegler, Notices Amer. Math. Soc. 51 (8) (2004) 873-883.

관련도서

• [ConwaySloane] Sphere Packings, Lattices and Groups (Grundlehren der mathematischen Wissenschaften)
  • John Horton Conway, Neil J. A. Sloane
  • 이 분야의 가장 표준적인 도서
• 케플러의 추측