"렘니스케이트(lemniscate) 곡선의 길이와 타원적분"의 두 판 사이의 차이

2015년 4월 5일 (일) 03:59 판

개요

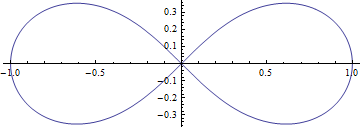
극좌표계에서 방정식 $r^2=\cos2\theta$ 로 주어진 곡선을 베르누이의 렘니스케이트 곡선이라 부름.
카테시안 좌표계에서는 $(x^2 + y^2)^2=x^2 - y^2$로 주어진다

렘니스케이트 곡선의 둘레의 길이와 타원적분

정리

렘니스케이트 곡선의 둘레의 길이 $L$은 타원적분으로 표현되며 다음이 성립한다 \[L=4\int_0^1\frac{dx}{\sqrt{1-x^4}}=2\sqrt{2}K(\frac{1}{\sqrt{2}})=5.2441\cdots\] 여기서 $K$는 제1종타원적분 K (complete elliptic integral of the first kind) $$K(k) = \int_0^{\frac{\pi}{2}} \frac{d\theta}{\sqrt{1-k^2 \sin^2\theta}}.$$ 또한 다음이 성립한다 \[L=B(1/2,1/4)=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}=\frac{\Gamma(1/4)^2}{\sqrt{2\pi}}\] 여기서 $B$는 오일러 베타적분(베타함수)이고, $\Gamma$는 감마함수

증명

렘니스케이트 곡선은 $x=r(\theta)\cos\theta,y=r(\theta)\sin\theta$로 매개화되며, 다음을 확인할 수 있다 $$ r'(\theta)=-\frac{\sin 2\theta}{r(\theta)} $$ 매개화를 이용하여, 둘레의 길이를 계산하면 다음을 얻는다 \[L=4\int_{0}^{\pi/4}\sqrt{r'(\theta)^2+r(\theta)^2}\,d\theta=4\int_{0}^{\pi/4}\sqrt{\frac{\sin^2 2\theta}{r^2(\theta)}+r^2(\theta)}\,d\theta=4\int_{0}^{\pi/4}\frac{1}{\sqrt{\cos 2\theta}}\,d\theta\] 이 때, $\cos 2\theta=\cos^2{\phi}$ 를 이용하여 치환하면, \[d\theta=\frac{\sin\phi\cos\phi}{\sqrt{1-\cos^4\phi}}\,d\phi=\frac{\cos\phi}{\sqrt{1+\cos^2\phi}}\,d\phi,\] \[L=4\int_0^{\pi/2}\frac{1}{\sqrt{1+\cos^2 \phi}}\,d\phi=2\sqrt{2}\int_0^{\pi/2}\frac{1}{\sqrt{1-\frac{1}{2}\sin^2 \phi}}\,d\phi \label{eq1}\] \ref{eq1}로부터 다음을 얻는다 $$ L=2\sqrt{2}K(1/\sqrt{2}) $$ \ref{eq1}에서 $x=\cos\phi$로 치환하면, \[L=4\int_0^{\pi/2}\frac{1}{\sqrt{1+\cos^2 \phi}}\,d\phi=4\int_0^1\frac{dx}{\sqrt{1-x^4}}=B(1/2,1/4)=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}=\frac{\Gamma(1/4)^2}{\sqrt{2\pi}}=5.2441\] ■

가우스의 렘니스케이트 상수

렘니스케이트 상수 $\omega$를 다음과 같이 정의

\[\omega:=2\int_0^1\frac{dx}{\sqrt{1-x^4}}=2.62\cdots\]

수론적 성질에 대해서는 가우스의 렘니스케이트 상수 항목 참조

재미있는 사실

곡선의 모양이 무한대 기호와 같음
무한대는 그 한계가 없기에 리본을 뜻하는 'lemniscus'라는 말로 불릴 때도 있었으며, 그로인해 무한대 기호가 누운 8자 모양이 되었다는 설이 있음

역사

1684 베르누이 'Acta Eruditorum'
18세기 Fagnano, Euler, and Legendre 에 의한 연구
1798~1799년 가우스가 $\pi/\omega$가 1과 $\sqrt2$의 산술 기하 평균 (arithmetic-geometric mean)이 됨을 관찰
수학사 연표

수학용어번역

http://www.google.com/dictionary?langpair=en|ko&q=lemniscate
Latin lemniscus meaning "ribbon"
번역용어제안
- 쌍타원, 겹타원, 이중타원, 나비리본
- '베르누이의 연주형'(lemniscate) http://www.google.com/dictionary?langpair=ko|ko&q=연주
lemniscate - 대한수학회 수학용어집

매스매티카 파일 및 계산 리소스

https://docs.google.com/leaf?id=0B8XXo8Tve1cxZjRmZjkwMjgtNGY0Mi00MzllLWExMGQtZjExZjIzZWMyNDRk&sort=name&layout=list&num=50

사전 형태의 자료

리뷰, 에세이, 강의노트

From Lintearia to Lemniscate I : physics to mathematics R Sridharan
From Lintearia to Lemniscate II: Gauss and Landen’s Work R Sridharan
The Lemniscate and Fagnano's Contributions to Elliptic IntegralsRaymond Ayoub, Archive for History of Exact Sciences, 1984

@@ 44번째 줄: / 44번째 줄: @@
 ==재미있는 사실==
-*  곡선의 모양이 무한대 기호와 같음
+* 곡선의 모양이 무한대 기호와 같음
-*  무한대는 그 한계가 없기에 리본을 뜻하는 'lemniscus'라는 말로 불릴 때도 있었으며, 그로인해 무한대 기호가 누운 8자 모양이 되었다는 설이 있음
+* 무한대는 그 한계가 없기에 리본을 뜻하는 'lemniscus'라는 말로 불릴 때도 있었으며, 그로인해 무한대 기호가 누운 8자 모양이 되었다는 설이 있음
+[[파일:렘니스케이트 반지.png|300px]]
 ==역사==