"프로듀스 X 101 투표 조작 논란"의 두 판 사이의 차이

2019년 7월 24일 (수) 04:58 판

개요

프로듀스 101 X 투표 조작 논란이 있다.
조작 논란의 근거는 득표수와 관련된 우연으로 보기 힘든 여러 현상들이다.
여러 번의 투표 결과를 득표수 그대로 더하지 않고, 적당히 가중치를 주어 합산하는 과정이 있었다면, 위에서 발견된 현상들은 대체로 설명이 가능하다.
가령 네번의 투표가 있었고, 각 투표가 예를 들어 모두 25%만큼 기여하도록 해야 한다면, 득표결과에 적당한 수를 곱하고 반올림하는 과정을 거쳤을 수도 있다.
7월 24일 엠넷이 내놓은 "득표수로 순위를 집계한 뒤 득표율로 계산해 소수점 둘째 자리로 반올림하고 이를 다시 득표수로 환산했다"는 해명은 따라서 납득할만하다.
단, 이 글은 투표 결과에 어떤 조작도 없었음을 증명하지는 않는다

설명

득표수와 관련된 많은 현상을 설명할 수 있는 하나의 수학적 명제가 있다.

마스터 정리

정리

0보다 큰 실수 $\alpha$가 주어져 있고, $\alpha$의 정수부분을 $f$라 하자. 임의의 자연수 $n$에 대하여, $n\alpha$를 반올림해서 얻어지는 자연수 $m$는 $f$의 배수와 $(f+1)$의 배수의 합으로 표현된다.

예

$\alpha=7494.442$
$f=7494$

다음과 같은 선택을 해보자.

$n=178$
$n\alpha=1334010.676$

그러면 $n\alpha$를 반올림하여, $m=1334011$이고 $m=1334011 = 99 \times 7494 + 79 \times 7495$

또 다른 예를 들자면,

$n=102$
$n\alpha=764433.084$

그러면 $n\alpha$를 반올림하여, $m=764433$이고 $m=764433 = 57 \times 7494 + 45 \times 7495$

예

$\alpha=5.2$
$f=5$
$n=3$
$n\alpha=15.6$

이 때, $m=16$이고, $16 = 2\times 5 + 1 \times 6$

프듀101 X 득표 테이블

이 글 https://gall.dcinside.com/board/view/?id=producex&no=2998354 에서 지적되었듯이, 프듀의 득표 테이블은 $\alpha=7494.442$에 적당한 자연수 $n$를 곱한 다음 반올림하여 얻어진 것과 12위 딱 한 곳만 제외하고 모두 같다. 12위의 표는 오타로 보는 것이 맞을 것이다. 맨 오른쪽에는 위에서 설명한 정리에서 처럼 7494와 7495의 배수의 합으로 이 수를 나타낸 것이다.

\begin{array}{c|cc|c} \text{} & \text{n} & \text{round} (n \alpha ) & \text{} \\ \hline 1 & 178 & 1334011 & 99*7494+79*7495 \\ 2 & 174 & 1304033 & 97*7494+77*7495 \\ 3 & 144 & 1079200 & 80*7494+64*7495 \\ 4 & 140 & 1049222 & 78*7494+62*7495 \\ 5 & 124 & 929311 & 69*7494+55*7495 \\ 6 & 110 & 824389 & 61*7494+49*7495 \\ 7 & 106 & 794411 & 59*7494+47*7495 \\ 8 & 102 & 764433 & 57*7494+45*7495 \\ 9 & 101 & 756939 & 56*7494+45*7495 \\ 10 & 100 & 749444 & 56*7494+44*7495 \\ 11 & 96 & 719466 & 54*7494+42*7495 \\ 12 & 94 & 704478 & 52*7494+42*7495 \\ 13 & 92 & 689489 & 51*7494+41*7495 \\ 14 & 90 & 674500 & 50*7494+40*7495 \\ 15 & 74 & 554589 & 41*7494+33*7495 \\ 16 & 64 & 479644 & 36*7494+28*7495 \\ 17 & 63 & 472150 & 35*7494+28*7495 \\ 18 & 62 & 464655 & 35*7494+27*7495 \\ 19 & 48 & 359733 & 27*7494+21*7495 \\ 20 & 38 & 284789 & 21*7494+17*7495 \\ \end{array}

토니의 득표수와 관련된 미스테리

20위 토니와 18위의 득표수의 합은 $284789 + 464655=749444$로 10위의 득표수와 같다. 일반적으로 7494와 7495의 배수의 합으로 표현되는 두 수의 합도 역시 7494와 7495의 배수의 합으로 표현가능하다. 대수적으로 표현하면 다음과 같다 :

$$ (7494a+7495b)+(7494c+7495d) = 7494(a+c)+7495(b+d). $$

따라서 둘의 득표수를 더해서 다른 사람의 득표가 나오는 것도 일어날 수 있는 일이 일어난 것이다. 꼭 20등 토니가 아니더라도 6등과 16등의 표를 더해 2등의 표가 나오는 일도 발생했다.

아래의 표는 a등의 표와 b등의 표를 더했을 때, c등의 표가 나온 경우를 모두 나열한 것이다.

\begin{array}{cc|c} a & b & c \\ \hline 4 & 20 & 1 \\ 6 & 16 & 2 \\ 7 & 20 & 3 \\ 8 & 20 & 4 \\ 10 & 15 & 2 \\ 13 & 19 & 4 \\ 16 & 20 & 8 \\ 17 & 20 & 9 \\ 18 & 20 & 10 \\ 19 & 19 & 11 \\ \end{array}

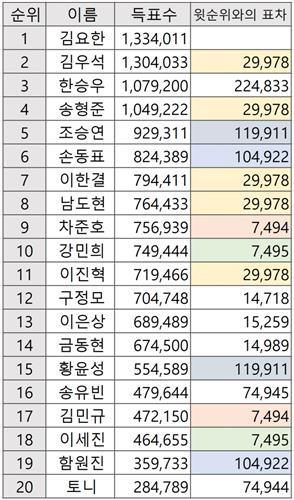
윗순위와의 표차

1위와 2위의 표차이는 29978이다. 이 수는 7494와 7495의 배수의 합으로 표현되는 두 수의 차이이므로, 역시 7494와 7495의 배수의 합으로 표현가능하다. 대수적으로 표현하면 다음과 같다 :

$$ (7494a+7495b)-(7494c+7495d) = 7494(a-c)+7495(b-d). $$

표는 다음과 같다. \begin{array}{ccc} \text{} & n & \text{round} (n \alpha ) \\ \hline 1 & 29978 & 2*7494+2*7495 \\ 2 & 224833 & 17*7494+13*7495 \\ 3 & 29978 & 2*7494+2*7495 \\ 4 & 119911 & 9*7494+7*7495 \\ 5 & 104922 & 8*7494+6*7495 \\ 6 & 29978 & 2*7494+2*7495 \\ 7 & 29978 & 2*7494+2*7495 \\ 8 & 7494 & 1*7494+0*7495 \\ 9 & 7495 & 0*7494+1*7495 \\ 10 & 29978 & 2*7494+2*7495 \\ 11 & 14988 & 2*7494+0*7495 \\ 12 & 14989 & 1*7494+1*7495 \\ 13 & 14989 & 1*7494+1*7495 \\ 14 & 119911 & 9*7494+7*7495 \\ 15 & 74945 & 5*7494+5*7495 \\ 16 & 7494 & 1*7494+0*7495 \\ 17 & 7495 & 0*7494+1*7495 \\ 18 & 104922 & 8*7494+6*7495 \\ 19 & 74944 & 6*7494+4*7495 \\ \end{array}

따라서 이 현상도 역시 일어날 수 있는 일이 일어난 것이다.

@@ 3번째 줄: / 3번째 줄: @@
 * 조작 논란의 근거는 득표수와 관련된 우연으로 보기 힘든 여러 현상들이다.
 * 여러 번의 투표 결과를 득표수 그대로 더하지 않고, 적당히 가중치를 주어 합산하는 과정이 있었다면, 위에서 발견된 현상들은 대체로 설명이 가능하다.
-* 가령 네번의 투표가 있었다면, 각 투표가 예를 들어 모두 25%만큼 기여하도록 해야 한다면, 득표결과에 적당한 수를 곱하고 반올림하는 과정을 거쳤을 수도 있다.
+* 가령 네번의 투표가 있었고, 각 투표가 예를 들어 모두 25%만큼 기여하도록 해야 한다면, 득표결과에 적당한 수를 곱하고 반올림하는 과정을 거쳤을 수도 있다.
 * 7월 24일 엠넷이 내놓은 "득표수로 순위를 집계한 뒤 득표율로 계산해 소수점 둘째 자리로 반올림하고 이를 다시 득표수로 환산했다"는 해명은 따라서 납득할만하다.
 * 단, 이 글은 투표 결과에 어떤 조작도 없었음을 증명하지는 않는다