"이차곡선(원뿔곡선)"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
잔글 (찾아 바꾸기 – “수학사연표” 문자열을 “수학사 연표” 문자열로)
11번째 줄: 11번째 줄:
 
==원뿔곡선==
 
==원뿔곡선==
  
−
*  원뿔의 축과 단면이 이루는 각도에 따라 다른 곡선들이 얻어진다<br>
+
*  원뿔의 축과 단면이 이루는 각도에 따라 다른 곡선들이 얻어진다
 
** 원 : 축과 단면이 수직인 경우에 얻어짐
 
** 원 : 축과 단면이 수직인 경우에 얻어짐
 
** 쌍곡선 : 축과 단면이 평행한 경우에 얻어짐
 
** 쌍곡선 : 축과 단면이 평행한 경우에 얻어짐
26번째 줄: 26번째 줄:
  
 
* 원뿔곡선의 방정식은 일반적으로 좌표평면에서 <math>ax^2+bxy+cy^2+dx+ey+f=0</math> 형태로 주어지며, 이차곡선이라 부르기도 한다
 
* 원뿔곡선의 방정식은 일반적으로 좌표평면에서 <math>ax^2+bxy+cy^2+dx+ey+f=0</math> 형태로 주어지며, 이차곡선이라 부르기도 한다
−
* <math>ax^2+bxy+cy^2+dx+ey+f=0</math>형태로 주어진 이차식(즉 <math>a, b, c</math>중 적어도 하나는 0이 아닌 경우)은 다음과 같은 경우로 나눠진다<br>
+
* <math>ax^2+bxy+cy^2+dx+ey+f=0</math>형태로 주어진 이차식(즉 <math>a, b, c</math>중 적어도 하나는 0이 아닌 경우)은 다음과 같은 경우로 나눠진다
 
** 공집합 ( <math>x^2+y^2=-1</math>)
 
** 공집합 ( <math>x^2+y^2=-1</math>)
 
** 두 직선 (<math>x^2-y^2=0</math>)
 
** 두 직선 (<math>x^2-y^2=0</math>)
34번째 줄: 34번째 줄:
 
** 쌍곡선 (<math>x^2-y^2=1</math>)
 
** 쌍곡선 (<math>x^2-y^2=1</math>)
 
* 판별식 <math>\Delta=b^2-4ac</math>
 
* 판별식 <math>\Delta=b^2-4ac</math>
−
*  이차식이 이차곡선을 나타내는 경우(즉 공집합이나, 두 직선을 표현하는 경우가 아닐때), 판별식을 통하여 이차곡선이 무엇인지를 알 수있다<br>
+
*  이차식이 이차곡선을 나타내는 경우(즉 공집합이나, 두 직선을 표현하는 경우가 아닐때), 판별식을 통하여 이차곡선이 무엇인지를 알 수있다
 
** <math>\Delta<0</math>인 경우, 타원. 이 때, <math>a=c</math>인 경우는 원
 
** <math>\Delta<0</math>인 경우, 타원. 이 때, <math>a=c</math>인 경우는 원
 
** <math>\Delta=0</math>인 경우, 포물선
 
** <math>\Delta=0</math>인 경우, 포물선
47번째 줄: 47번째 줄:
 
==이심률==
 
==이심률==
  
−
* [[타원]] 의 이심률:<math>\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, (a>b>0)</math> 으로 주어진 타원의 이심률은 <math>\frac{\sqrt{a^2-b^2}}{a}</math><br>
+
* [[타원]] 의 이심률:<math>\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, (a>b>0)</math> 으로 주어진 타원의 이심률은 <math>\frac{\sqrt{a^2-b^2}}{a}</math>
  
 
   
 
   
75번째 줄: 75번째 줄:
 
==== 하위페이지 ====
 
==== 하위페이지 ====
  
−
* [[이차곡선(원뿔곡선)]]<br>
+
* [[이차곡선(원뿔곡선)]]
−
** [[쌍곡선]]<br>
+
** [[쌍곡선]]
−
** [[이차곡선과 회전변환]]<br>
+
** [[이차곡선과 회전변환]]
−
** [[타원]]<br>
+
** [[타원]]
−
** [[포물선]]<br>
+
** [[포물선]]
  
 
   
 
   
97번째 줄: 97번째 줄:
 
==관련된 개념 및 나중에 더 배우게 되는 것들==
 
==관련된 개념 및 나중에 더 배우게 되는 것들==
  
−
*  변환<br>
+
*  변환
 
** 평행이동
 
** 평행이동
 
** 회전변환
 
** 회전변환
105번째 줄: 105번째 줄:
 
==관련있는 다른 과목==
 
==관련있는 다른 과목==
  
−
*  물리<br>
+
*  물리
 
** [[케플러의 법칙, 행성운동과 타원|행성운동과 타원]]
 
** [[케플러의 법칙, 행성운동과 타원|행성운동과 타원]]
−
*  미술<br>
+
*  미술
 
** 원근법
 
** 원근법
 
** [[타원과 인간]]
 
** [[타원과 인간]]
115번째 줄: 115번째 줄:
 
==관련된 대학교 수학==
 
==관련된 대학교 수학==
  
−
* [[선형대수학]]<br>
+
* [[선형대수학]]
 
** 대칭행렬의 대각화
 
** 대칭행렬의 대각화
 
** 고유벡터, 고유값
 
** 고유벡터, 고유값
 
** 이차형식의 대각화
 
** 이차형식의 대각화
−
* [[대수기하학]]<br>
+
* [[대수기하학]]
 
** 다항식으로 정의되는 도형에 대한 일반화 및 체계적인 공부
 
** 다항식으로 정의되는 도형에 대한 일반화 및 체계적인 공부
  
135번째 줄: 135번째 줄:
 
* http://www.wolframalpha.com/input/?i=
 
* http://www.wolframalpha.com/input/?i=
 
* [http://dlmf.nist.gov/ NIST Digital Library of Mathematical Functions]
 
* [http://dlmf.nist.gov/ NIST Digital Library of Mathematical Functions]
−
* [http://www.research.att.com/%7Enjas/sequences/index.html The On-Line Encyclopedia of Integer Sequences]<br>
+
* [http://www.research.att.com/%7Enjas/sequences/index.html The On-Line Encyclopedia of Integer Sequences]
 
** http://www.research.att.com/~njas/sequences/?q=
 
** http://www.research.att.com/~njas/sequences/?q=
  
153번째 줄: 153번째 줄:
 
==블로그==
 
==블로그==
  
−
* [http://bomber0.byus.net/index.php/2008/01/06/508 원뿔곡선 vs 이차곡선]<br>
+
* [http://bomber0.byus.net/index.php/2008/01/06/508 원뿔곡선 vs 이차곡선]
 
** 피타고라스의 창
 
** 피타고라스의 창
  
160번째 줄: 160번째 줄:
 
==동영상 강좌==
 
==동영상 강좌==
  
−
* [http://news.chosun.com/site/data/html_dir/2007/07/05/2007070500023.html [한석원의 수리논술] 포물선과 쌍곡선의 성질]<br>
+
* [http://news.chosun.com/site/data/html_dir/2007/07/05/2007070500023.html [한석원의 수리논술] 포물선과 쌍곡선의 성질]
−
**  조x일보, 2007.07.05 <br>
+
**  조x일보, 2007.07.05  
 
[[분류:곡선]]
 
[[분류:곡선]]
 
[[분류:고교수학]]
 
[[분류:고교수학]]

2020년 11월 16일 (월) 06:41 판

개요

  • 원뿔의 단면을 통해서 얻어지는 곡선이라서, 원뿔곡선 또는 원추곡선이라 불려진다
  • 평면상에서 곡선의 방정식이 \(ax^2+bxy+cy^2+dx+ey+f=0\)의 형태로 주어지기 때문에, 이차곡선이라고 부름.
  • 이 두 가지 관점을 모두 가지고 이해하는 것이 좋다.



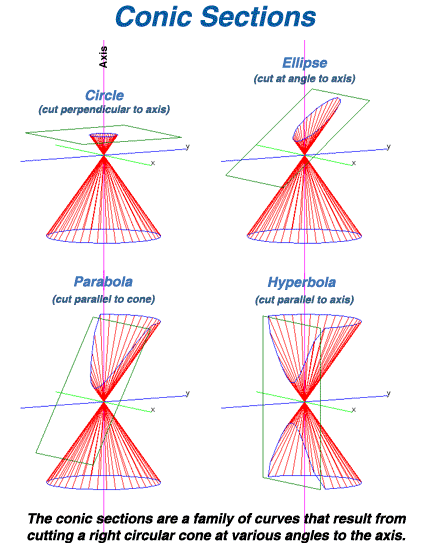
원뿔곡선

  • 원뿔의 축과 단면이 이루는 각도에 따라 다른 곡선들이 얻어진다
    • 원 : 축과 단면이 수직인 경우에 얻어짐
    • 쌍곡선 : 축과 단면이 평행한 경우에 얻어짐
    • 타원 : 축과 단면이 수직, 평행하지 않고, 원뿔의 모선과 평행하지 않은 경우에 얻어짐
    • 포물선 : 단면이 원뿔의 모선과 평행한 경우에 얻어짐

1999008-p108.gif



곡선의 방정식과 이차곡선

  • 원뿔곡선의 방정식은 일반적으로 좌표평면에서 \(ax^2+bxy+cy^2+dx+ey+f=0\) 형태로 주어지며, 이차곡선이라 부르기도 한다
  • \(ax^2+bxy+cy^2+dx+ey+f=0\)형태로 주어진 이차식(즉 \(a, b, c\)중 적어도 하나는 0이 아닌 경우)은 다음과 같은 경우로 나눠진다
    • 공집합 ( \(x^2+y^2=-1\))
    • 두 직선 (\(x^2-y^2=0\))
    • 포물선 (\(x^2-y=0\))
    • 타원 (\(2x^2+y^2=1\))
    • 원 (\(x^2+y^2=1\))
    • 쌍곡선 (\(x^2-y^2=1\))
  • 판별식 \(\Delta=b^2-4ac\)
  • 이차식이 이차곡선을 나타내는 경우(즉 공집합이나, 두 직선을 표현하는 경우가 아닐때), 판별식을 통하여 이차곡선이 무엇인지를 알 수있다
    • \(\Delta<0\)인 경우, 타원. 이 때, \(a=c\)인 경우는 원
    • \(\Delta=0\)인 경우, 포물선
    • \(\Delta>0\)인 경우, 쌍곡선
  • http://www.mecca.org/~halfacre/MATH/rotation.htm
  • http://home.scarlet.be/math/reduc.htm



이심률

  • 타원 의 이심률\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, (a>b>0)\] 으로 주어진 타원의 이심률은 \(\frac{\sqrt{a^2-b^2}}{a}\)



이차곡선을 판별하는 알고리즘

  • 이차식 \(ax^2+bxy+cy^2+dx+ey+f=0\)이 주어진 경우



역사



하위페이지




관련된 항목들



관련된 개념 및 나중에 더 배우게 되는 것들

  • 변환
    • 평행이동
    • 회전변환


관련있는 다른 과목


관련된 대학교 수학

  • 선형대수학
    • 대칭행렬의 대각화
    • 고유벡터, 고유값
    • 이차형식의 대각화
  • 대수기하학
    • 다항식으로 정의되는 도형에 대한 일반화 및 체계적인 공부



사전 형태의 자료



관련논문



블로그


동영상 강좌

원본 주소 "https://wiki.mathnt.net/index.php?title=이차곡선(원뿔곡선)&oldid=45250"