2012년 대선 개표와 로지스틱 곡선

수학노트
Pythagoras0 (토론 | 기여)님의 2012년 12월 31일 (월) 17:37 판
둘러보기로 가기 검색하러 가기

개요

  • 다음 아고라를 중심으로 2012년 대선 개표에 부정이 있다는 주장을 담은 글들이 올라옴
  • 특히 '그루터기추억'이 작성한 글들은 대선 개표와 로지스틱 함수를 연관시켜 화제가 되고 주목을 받음
    • 여러 글에 걸쳐 있을 수 없는 일이 일어났다는 식의 주장을 내놓고, 그에 대한 근거라며 이러저러한 계산 결과와 수치들을 제시함
  • 검토 후 판단
    • 개표 부정이라며 제시하는 현상이 수학/통계에 훈련된 사람이라면 대개 자연스럽다거나 또는 특별할 것이 없다고 여겨지는 것들
    • 아무런 의미가 없거나(로지스틱 확률함수 $p$), 놀라울 게 없는 계산(다항식을 이용한 보간 등)을 해놓고 엄청난 일처럼 이야기를 함
    • 수학/통계에 대한 이해가 별로 없는 사람들에게 개표 부정에 대한 불안감을 증폭시키고 있으니 주의를 요망함


'그루터기추억' 글 중에서도 가장 화제가 된 글의 삽질


그루터기추억의 $p$와 $f$

  • 집합 $\{1,2,\cdots, 21\}$ 를 정의역으로 하는 두 함수 $f,g$에 대하여, 함수 $p$를 다음과 같이 정의하자

$$ p(t):=\frac{f(1) f(t) g(t)}{f(1) (g(t)-1)+f(t)} $$

  • 이 정의로부터 다음을 얻는다 (일명 그루터기추억의 항등식)

$$\label{fep} f(t)=\frac{p(1) (1-g(t)) p(t)}{p(t)-p(1) g(t)} $$

  • 중요한 점은 함수 $g$가 주어져 있기만 한다면 그게 무엇이든 상관없이 $f$로부터 $p$를 계산할 수 있고, 마찬가지로 $p$로부터 $f$를 계산할 수 있다는 사실.
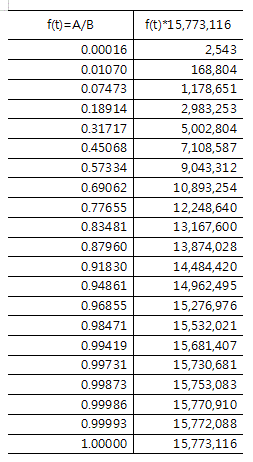
  • 이 글에서 $f(t)$는 박근혜 후보의 시간 $t$에서의 누적득표수의 비율로 다음 표로 제시됨

박근혜 후보의 시간대별 득표수와 비율.gif

  • $g(t)=e^t$ 가 사용되었고, 여기서 로지스틱 확률함수라고 부르는 $p(t)$가 계산된 것임.
  • $g(t)=e^t$ 의 선택 때문에 $p$의 그래프가 로지스틱 곡선과 비슷하게 나타남.


로지스틱 음모가 아니라 혹시 사인 음모론은 아닌가

  • $g$를 다른 함수로 선택하면, $p$ 역시 다른 함수가 될 것임.
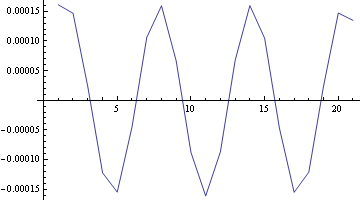
  • 가령 $g(t)=\sin t$로 두면, $p$의 (적당한 내삽을 거쳐) 그래프는 다음과 같이 주어짐

2012년 대선 개표와 로지스틱 곡선1.gif

  • 물론 이 $p(t)$를 가지고도, 그루터기추억의 항등식 \ref{fep}을 사용하여 박근혜 후보의 시간대별 누적득표수를 완벽하게 계산할 수 있음
  • 그러면 이것은 로지스틱 음모론이 아니라 사인 음모론인가?


요약정리

  • 이 글에서 제시된 시간대별 로지스틱 확률함수 $p(t)$라는 것은 $g$가 지수함수이기 때문에 로지스틱 곡선의 모양을 하게 된 것뿐임
  • 가령, $g$를 사인함수로 선택하면, $p$는 사인곡선 모양을 함
  • 거창하게 로지스틱 확률함수 $p$라고 이름을 붙였으나, $g$와 $p$는 아무런 쓸모가 없는 무의미한 것들
  • 그냥 뻘 계산을 담고 있는 헛소리임


시간-누적득표 곡선이 S자 형태가 되는 것은 놀라운 일인가

  • 결론부터 말하면 별로 놀라울 것이 없음


S자 곡선에 대한 직관적인 이해

  • 수식을 쓰지 않아도, 이를 이해하는 것은 크게 어렵지 않음
  • 개표작업이 시간에 따라 어떻게 변하는지를 이해하기
    • 개표가 시작되기 전에는 기울기가 0인 직선
    • 개표소에 따라 차이를 갖고 개표 작업이 시작되면서 기울기가 점차 증가하기 시작함
    • 모든 개표소의 작업이 궤도에 오르면 기울기는 상당히 안정된 범위에 들어가게 됨
    • 개표소에 따라 개표가 점차 마무리 단계에 접어들면 기울기가 줄어들기 시작함
    • 개표가 끝난 후에는 기울기가 0
  • 이러한 조건을 만족시키는 가장 간단하고 직관적인 곡선이라면 S자 형태의 로지스틱 곡선이 될 것임

곡선 접합(curve fitting)의 계산

  • 수학이나 통계용 소프트웨어를 사용하면 데이터에 대한 곡선 접합을 어렵지 않게 얻을 수 있음
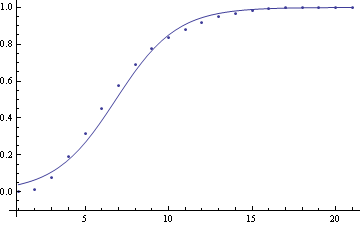
  • 시간-누적득표 곡선은 직관대로 그럴듯한 로지스틱 곡선 접합을 찾을 수 있음

2012년 대선 개표와 로지스틱 곡선3.gif

  • 하지만 그것이 수학적으로 완벽한 로지스틱 곡선이라는 주장의 상당 부분은 위에서 검토한 그루터기추억의 뻘 계산에서 온 오해
  • 위에 $f$로 제시된 시간에 따른 누적득표 비율은, 개표가 거의 마무리된 단계, 즉 기울기가 0에 가까운 부분들이 많이 포함되어 있어 더 좋은 로지스틱 곡선 접합이 얻어짐
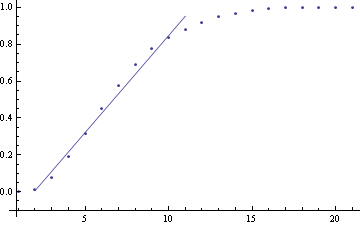
  • 기울기가 안정된 가운데 부분들만 놓고 본다면 좋은 선형성을 가짐

2012년 대선 개표와 로지스틱 곡선2.gif


관련된 항목들


계산 리소스


다음 아고라의 글

그루터기추억의 글


메모

  • David Arnold, Fitting a Logistic Curve to Data, February 24, 2002
  • Kumar, K. 1998. “82.44 Fitting of Sigmoidal Growth Curves.” The Mathematical Gazette 82 (494) (July 1): 306–309. doi:10.2307/3620427.
  • Cavallini, Fabio. 1993. “Fitting a Logistic Curve to Data.” The College Mathematics Journal 24 (3) (May 1): 247–253. doi:10.2307/2686488.
원본 주소 "https://wiki.mathnt.net/index.php?title=2012년_대선_개표와_로지스틱_곡선&oldid=24672"