교차비(cross ratio)
Pythagoras0 (토론 | 기여)님의 2012년 12월 22일 (토) 13:01 판
이 항목의 스프링노트 원문주소
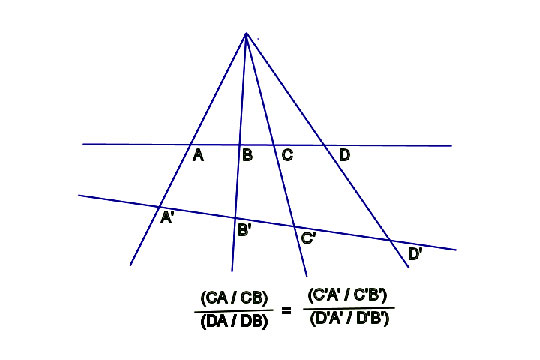
교차비
- 사영기하학의 기본개념
- 네 복소수 \(z_1,z_2,z_3,z_4\)에 대하여 다음과 같이 정의됨.
\((z_1,z_2;z_3,z_4) = \frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)}\)
- \(z_4=\infty\) 인 경우
\((z_1,z_2;z_3,\infty) = \frac{(z_1-z_3)}{(z_2-z_3)}\)
대칭군과 교차비
- 대칭군 (symmetric group)은 \(\{1,2,3,4\}\)에 작용한다
- 이 때 조화비는 다음과 같이 변한다
\((z_1, z_2; z_3, z_4) = \lambda\\)
\((z_1, z_2; z_4, z_3) = {1\over\lambda}\)
\((z_1, z_3; z_4, z_2) = {1\over{1-\lambda}}\)
\((z_1, z_3; z_2, z_4) = 1-\lambda\)
\((z_1, z_4; z_3, z_2) = {\lambda\over{\lambda-1}}\)
\((z_1, z_4; z_2, z_3) = {{\lambda-1}\over\lambda}\) - 즉 대칭군에 의해 다음 값을 가질 수 있다
\( \lambda, {1\over\lambda},{1\over{1-\lambda}}, 1-\lambda, {\lambda\over{\lambda-1}}, {{\lambda-1}\over\lambda}\)
사영기하학과 교차비
관련된 항목들
매스매티카 파일 및 계산 리소스
- https://docs.google.com/leaf?id=0B8XXo8Tve1cxY2Y4OWEwNWMtMGU0Zi00NTEwLTlkYjctZWE3NDE0YTA2YmM2&sort=name&layout=list&num=50
- http://www.wolframalpha.com/input/?i=
- http://functions.wolfram.com/
- NIST Digital Library of Mathematical Functions
- Abramowitz and Stegun Handbook of mathematical functions
- The On-Line Encyclopedia of Integer Sequences
- Numbers, constants and computation
- 매스매티카 파일 목록
수학용어번역
- cross ratio
- 비조화비, 복비
- http://www.google.com/dictionary?langpair=en%7Cko&q=
- 대한수학회 수학 학술 용어집
- 대한수학회 수학용어한글화 게시판
사전 형태의 자료
- http://ko.wikipedia.org/wiki/
- http://en.wikipedia.org/wiki/cross_ratio
- [1]http://mathworld.wolfram.com/CrossRatio.html