등시강하곡선 문제 (Tautochrone problem)

개요

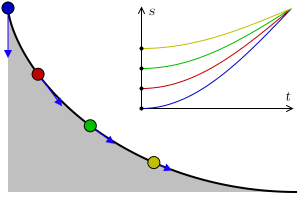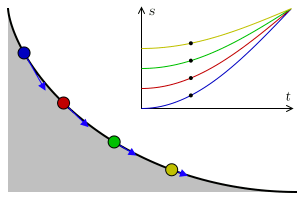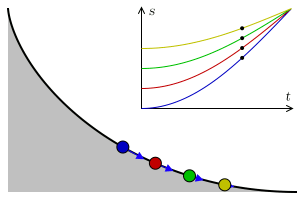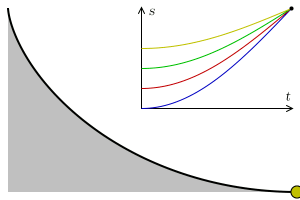
중력을 받고 있는 물체가 출발점에 관계없이 주어진 목적지에 똑같은 시간에 도달하기 위해서 따라야 하는 곡선
사이클로이드에 의하여 만족됨
1659년 호이겐스에 의해 해결
진자 시계를 만드는데 활용되었다 http://hom.wikidot.com/the-cycloid

등시성의 증명

(정리) 사이클로이드를 따라 움직이는 추의 주기는 시작점의 위치에 관계없이 다음으로 주어진다. \[T =2\pi\sqrt{\frac{r}{g}}\]

(이 때, 사이클로이드의 방정식은 \(x = r(\theta - \sin \theta)\), \(y = -r(1 - \cos \theta)\)로 주어졌다고 하자.)

(증명)

출발점의 y좌표를 \(y=y_0\)라 두고, 그 때 곡선의 파라메터를 \(\theta=\theta_0\)라 하자.

움직이는 추의 속도는 \(v=\sqrt{2g(y_0-y)}= \sqrt{2rg(\cos\theta_0-\cos\theta)}\) 로 주어진다. 따라서 주기를 다음과 같이 쓸 수 있다 \[T =\int \frac{ds}{v}=2\int_{\theta_0}^{\pi} \frac{\sqrt{2r^2(1-\cos\theta)}}{\sqrt{2rg(\cos\theta_0-\cos\theta)}}\,d\theta=2\sqrt{\frac{r}{g}}\int_{\theta_0}^{\pi} \frac{\sqrt{1-\cos\theta}}{\sqrt{\cos\theta_0-\cos\theta}}\,d\theta \label{vel}\]

반각공식을 이용하여, \ref{vel}의 우변을 다음과 같이 쓸 수 있다

\[2\sqrt{\frac{r}{g}}\int_{\theta_0}^{\pi}\frac{\sin(\frac{1}{2}\theta)}{\sqrt{\cos^2(\frac{1}{2}\theta_0)-\cos^2(\frac{1}{2}\theta)}}d\theta \] 여기서 \[u=\frac{\cos \frac{1}{2}\theta}{\cos \frac{1}{2}\theta_0}\]로 치환하면, \[du=\frac{-\sin \frac{1}{2}\theta}{2\cos \frac{1}{2}\theta_0}\,d\theta\] 를 얻는다.

따라서 \[T =4\sqrt{\frac{r}{g}}\int_{0}^{1} \frac{1}{\sqrt{1-u^2}}\,du=2\pi\sqrt{\frac{r}{g}}\]■

메모

http://www.baropage.com/file_board/view.php?id=life02&page=1&sn1=&divpage=1&sn=off&ss=on&sc=on&select_arrange=hit&desc=desc&no=95

등시강하곡선 문제 (Tautochrone problem)

목차

개요

등시성의 증명

관련동영상

메모

역사

메모

관련된 항목들

매스매티카 파일 및 계산 리소스

수학용어번역

사전 형태의 자료

관련논문

둘러보기 메뉴

검색