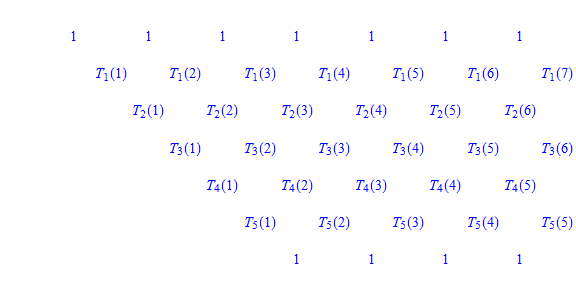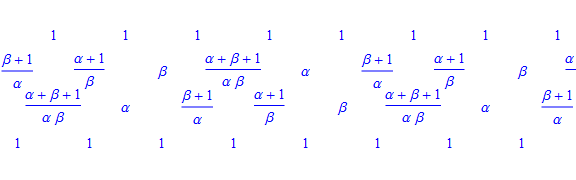콕세터 프리즈

개요

• 자연수 $r$, $I=\{1\,\cdots, r\}$
• 변수 $\left(Q^{(a)}_{m}\right)$, $m\in \mathbb{Z}_{\geq 0}$, $a\in I$에 대하여, 다음과 같은 점화식을 생각하자

\begin{equation} \label{cf} \left\{ \begin{array}{lll} Q^{(0)}_{m} =Q^{(r+1)}_{m} =1 & m\in \mathbb{Z}_{\geq 0} \\ Q^{(a)}_{m}Q^{(a)}_{m+1}=1+Q^{(a-1)}_{m+1}Q^{(a+1)}_{m} & a\in I, m\in \mathbb{Z}_{\geq 0} \end{array} \right. \end{equation}

• 아래의 그림은 $r=5$인 경우에 해당하며, $\left(Q^{(a)}_{1}\right)_{a\in I}$가 결정되면, 나머지 $Q^{(a)}_{m}$는 점화식 \ref{cf}로부터 얻어진다

• 점화식 \ref{cf}은 다음과 같은 배열이 $ad-bc=1$를 만족시키는 것으로 이해할 수 있다

예

성질

주기성

• 각 $a\in I$에 대하여, $Q^{(a)}_{m+(r+3)}=Q^{(a)}_{m}$이 성립한다

매스매티카 파일 및 계산 리소스

• https://docs.google.com/file/d/0B8XXo8Tve1cxbjhtOHUwbTB1S2s/edit?usp=drivesdk

관련논문

• Conway, J. H., and H. S. M. Coxeter. 1973. “Triangulated Polygons and Frieze Patterns.” The Mathematical Gazette 57 (400) (June 1): 87–94. doi:10.2307/3615344.
• Conway, J. H., and H. S. M. Coxeter. 1973. “Triangulated Polygons and Frieze Patterns (Continued).” The Mathematical Gazette 57 (401) (October 1): 175–183. doi:10.2307/3615561.
• Coxeter, H. S. M. 1971. “Frieze Patterns.” Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica 18: 297–310. https://eudml.org/doc/204992