Lectures on dilogarithm function

overview

dilogarithm function
Bloch-Wigner dilogarithm function
Bloch group
values of the Dedekind zeta function at s=2
volumes of hyperbolic 3-manifolds

dilogarithm fuction

Define

\[\operatorname{Li}_ 2(z)= \sum_{n=1}^\infty {z^n \over n^2},\, |z|<1\]

extend domain

\[\operatorname{Li}_ 2(z) = -\int_0^z{{\log (1-t)}\over t} dt,\, z\in \mathbb C\backslash [1,\infty) \]

functional equations

reflection properties

\[\mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)= -\frac{\pi^2}{6}-\frac{1}{2}\log^2(-z)\] \[\mbox{Li}_ 2(z)+\mbox{Li}_ 2(1-z)= \frac{\pi^2}{6}-\log(z)\log(1-z)\]

proof

\[f(z): = \mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)+\frac{1}{2}\log^2(-z)\] is constant as $f'(z)$ is $$ -\frac{\log (1-z)}{z}+\frac{\log \left(1-\frac{1}{z}\right)}{z}+\frac{\log (-z)}{z}=0 $$

When $z=-1$, \[\mbox{Li}_ 2(z)+\mbox{Li}_ 2(1/z)+\frac{1}{2}\log^2(-z) = 2\mbox{Li}_ 2(-1)\]

When $z=1$; \[2\mbox{Li}_ 2(1)+\frac{1}{2}\log^2(-1) = 2\mbox{Li}_ 2(-1)\] \[\frac{\pi^2}{3}-\frac{1}{2}\pi^2 = 2\mbox{Li}_ 2(-1)\]

■

five-term relation

\[\mbox{Li}_ 2(x)+\mbox{Li}_ 2(y)+\mbox{Li}_ 2 \left( \frac{1-x}{1-xy} \right)+\mbox{Li}_ 2(1-xy)+\mbox{Li}_ 2 \left( \frac{1-y}{1-xy} \right)=\text{something elementary}\]

Let us state this in terms of the Rogers dilogarithm (no worry about the branches) \[L(x): =\operatorname{Li}_ 2(x)+\frac{1}{2}\log x\log (1-x)=-\frac{1}{2}\int_{0}^{x}\left(\frac{\log(1-y)}{y}+\frac{\log(y)}{1-y}\right)dy,\, x\in (0,1)\]

$0\leq x,y\leq 1$

\[L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)=\frac{\pi^2}{2}\]

proof

Show that the partial derivatives of $F(x,y):=L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)$ are 0. Note $$ L(h(x))' = -\frac{h'(x) \log (1-h(x))}{2 h(x)}-\frac{h'(x) \log (h(x))}{2 (1-h(x))}. $$

$$ \begin{aligned} F_x = & \frac{1}{2} \left(\frac{\log (x)}{1-x}-\frac{\log (1-x)}{x}\right)+\frac{1}{2} \left(\frac{\log (1-x y)}{x}-\frac{y \log (x y)}{1-x y}\right)+0+\frac{(1-y) \log \left(\frac{1-y}{1-x y}\right)+(1-x) y \log \left(\frac{(1-x) y}{1-x y}\right)}{2 (1-x) (1-x y)}-\frac{(1-x) \log \left(\frac{1-x}{1-x y}\right)+x (1-y) \log \left(\frac{x (1-y)}{1-x y}\right)}{2 (1-x) x (1-x y)} \\ & =\frac{1}{2} \log (x)\left(\frac{1}{1-x}+\frac{-y}{1-xy}+\frac{-(1-y)}{(1-x) (1-x y)} \right)+\dots \end{aligned} $$ Do the same for $F_y$.

There is a more systematic way to control the cancellations.

Observe \[\frac{d}{dx}L(h(x))=\frac{1}{2}[\log(h(x))\frac{d}{dx}\log (1-h(x))-\log(1-h(x))\frac{d}{dx}\log h(x)]\]

For $f,g\in \mathbb{Q}(x,y)$, define (symbolically) $$ f\wedge g : = \log (f) d (\log (g))-\log (g) d (\log (f)) $$ where $df = f_x dx + f_y dy$.

For example, $L'(x)dx =\frac{1}{2} x\wedge (1-x) $

Then

$f\wedge g=-f \wedge g$
$(f_1f_2)\wedge g=f_1\wedge g+f_2\wedge g$

So $$ F_x dx+F_y dy = \frac{1}{2}\left(x\wedge (1-x)+(1-x y)\wedge (x y)+y\wedge (1-y)+\frac{1-y}{1-x y}\wedge \left(\frac{y(1-x)}{1-x y}\right)+\frac{1-x}{1-x y}\wedge \left(\frac{x(1-y)}{1-xy}\right) \right)=0 $$

remark

recurrence relation

\[1-x_{i}=x_{i-1}x_{i+1},\, x_0=x,\, x_2=y\]

5-periodic solution

\[x_0=x, x_1=1-xy, x_2=y, x_3=\frac{1-y}{1-xy}, x_4=\frac{1-x}{1-xy}\]

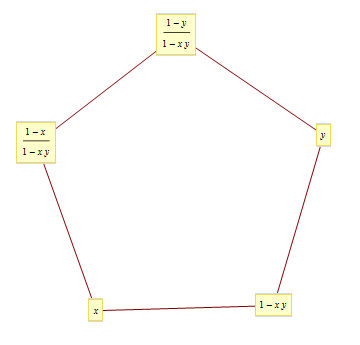
remark

we believe(?) all functional equations are coming from the five-term relation

remark

Zagier has $$ \frac{\pi^2}{6}-\log(x)\log(1-x)-\log(y)\log(1-y)+\log (\frac{1-x}{1-xy})\log (\frac{1-y}{1-xy}) $$ on the RHS, which is not correct

special values

$\mbox{Li}_{2}(0)=0$

$\mbox{Li}_{2}(1)=\frac{\pi^2}{6}$

$\mbox{Li}_{2}(-1)=-\frac{\pi^2}{12}$

$\mbox{Li}_{2}(\frac{1}{2})=\frac{\pi^2}{12}-\frac{1}{2}\log^2(2)$

$\mbox{Li}_{2}(\frac{3-\sqrt{5}}{2})=\frac{\pi^2}{15}-\log^2(\frac{1+\sqrt{5}}{2})$

$\mbox{Li}_{2}(\frac{-1+\sqrt{5}}{2})=\frac{\pi^2}{10}-\log^2(\frac{1+\sqrt{5}}{2})$

$\mbox{Li}_{2}(\frac{1-\sqrt{5}}{2})=-\frac{\pi^2}{15}+\frac{1}{2}\log^2(\frac{1+\sqrt{5}}{2})$

$\mbox{Li}_{2}(\frac{-1-\sqrt{5}}{2})=-\frac{\pi^2}{10}+\frac{1}{2}\log^2(\frac{1+\sqrt{5}}{2})$

Bloch-Wigner dilogarithm

$\operatorname{Li}_2(z)$ jumps by $2\pi i \log|z|$ as $z$ crosses the cut
consider $\operatorname{Li}_2(z)+i \log|z|\arg(1-z)$, where $-\pi <\arg z< \pi$
when it cross the line $(1,\infty)$, it becomes continuous

example

$$ \begin{aligned} \operatorname{Li}_2(2+0.001i) & = 2.46583 + 2.17759 i \\ \operatorname{Li}_2(2-0.001i) & = 2.46583 - 2.17759 i \end{aligned} $$ and $$ \begin{aligned} \log |(2+0.001i)| \arg(1-(2+0.001i)) & = 0. - 2.17689 i \\ \log |(2-0.001i)| \arg(1-(2-0.001i)) & = 0. + 2.17689 i \end{aligned} $$

define

$$D(z)=\text{Im}(\operatorname{Li}_2(z))+\log|z|\arg(1-z).$$

real analytic function on $\mathbb{C}$ except at 0 and 1, where it is continuous but not differentiable.
$D(\bar{z})=-D(z)$, and vanishes on $\mathbb{R}$.
It satisfies the following functional equations :

\begin{equation}\label{functid1} D(x)+D(1-xy)+D(y)+D(\frac{1-y}{1-xy})+D(\frac{1-x}{1-xy})=0, \end{equation} \begin{equation}\label{functid2} D(x)+D(1-x) =D(x)+D(\frac{1}{x})=0. \end{equation}

Bloch group

Let $\mathbb{F}$ be a field
$\Lambda^2({\mathbb{F}^{\times}})$ the set of all formal linear combinations $x\wedge y$, $x,y\in\mathbb{F^{\times}}$ subject to relations
- $a\wedge b=-b \wedge a$
- $(x_1x_2)\wedge y=x_1\wedge y+x_2\wedge y$
$\mathbb{Z}[\mathbb{F}^{\times}\backslash\{1\}]$
- i.e. abelian group of formal sums $[x_1]+[x_2]+\cdots+[x_n]$, $x_1,x_2,\cdots,x_n\in \mathbb{F}\backslash\{0,1\}$
$\partial : \mathbb{Z}[\mathbb{F}^{\times}\backslash\{1\}] \to \Lambda^2({\mathbb{F}^{\times}})$
- $[x]\to x\wedge (1-x)$
Let $\mathcal{A}(\mathbb{F})=\operatorname{ker}\partial$ and $\mathcal{C}(\mathbb{F})$ subgroup of $\mathcal{A}(\mathbb{F})=\operatorname{ker}\partial$ generated by

\[[x]+[1-xy]+[y]+[\frac{1-y}{1-xy}]+[\frac{1-x}{1-xy}]\]

The Bloch group is defined to be

\[\mathcal{B}(\mathbb{F})=\mathcal{A}(\mathbb{F})/\mathcal{C}(\mathbb{F})\]

$[x]+[1-x]$ is in $\mathcal{B}(\mathbb{F})$
Q. is $[x]+[\frac{1}{x}]$ in $\mathcal{B}(\mathbb{F})$?

example

$F=\mathbb{Q}(\sqrt{-7})$

$$ 2[\frac{1+\sqrt{-7}}{2}]+[\frac{-1+\sqrt{-7}}{4}]\in \mathcal{B}(F) $$

values of Dedekind zeta at s=2

Dedekind zeta

Let $K$ be a number field with $[K:\mathbb{Q}]=r_1+2r_2$
$\zeta _K(s):= \zeta_K (s) = \sum_{I \subseteq \mathcal{O}_K} \frac{1}{(N_{K/\mathbf{Q}} (I))^{s}}$
functional equation

\[\xi_{K}(s)=\left|d_K\right|{}^{s/2} 2^{r_2 (1-s)} \pi ^{\frac{1}{2} \left(-r_1-2 r_2\right) s}\Gamma \left(\frac{s}{2}\right)^{r_1} \Gamma (s)^{r_2}\zeta _K(s)\]\[\xi_{K}(s) = \xi_{K}(1 - s)\]

at $s=-n, n=1,2\cdots$, $\zeta_K(s)$ has zero of order $r_2$ or $r_1+r_2$ if $n$ is even or odd, respectively

$$ 2^{(m+1) r_2} \pi^{-\frac{1}{2} m \left(-r_1-2 r_2\right)}\zeta_K(-m) \Gamma (-m)^{r_2}\Gamma(-\frac{m}{2} )^{r_1} \left| d_K\right| {}^{-\frac{m}{2}}\\ =2^{-m r_2} \pi ^{\frac{1}{2} (m+1) \left(-r_1-2 r_2\right)} \zeta _K(m+1)\Gamma(\frac{m+1}{2})^{r_1}\Gamma (m+1)^{r_2} \left| d_K\right| {}^{\frac{m+1}{2}} $$

Dirichlet class number formula

residue at $s=1$

\[ \lim_{s\to 1} (s-1)\zeta_K(s)=\frac{2^{r_1}\cdot(2\pi)^{r_2}\cdot h_K\cdot R_K}{w_K \cdot \sqrt{|d_K|}}\]

equivalently, $\zeta _K(s)$ has zero of order $r_1+r_2-1$ at $s=0$

\[ \lim_{s\to 0}\frac{\zeta_K(s)}{s^{r_1+r_2-1}}=-\frac{h_K R_K}{w_K}\]

algebraic K-theory

$F$ : number field
$K_0(F) = \mathbb{Z}$
$K_1(F) = F^{\times}$
$K_2(F) = F^{\times}\otimes F^{\times}/\langle x\otimes (1-x) \rangle$
$K_0(\mathcal{O}_F) = \mathbb{Z}\oplus Cl_F$
$K_1(\mathcal{O}_F) = (\mathcal{O}_F)^{\times}$
$K_2(\mathcal{O}_F)$ : finite group

Borel's regulator

Borel constructed a map

$$ K_{2i-1}(F) \to \mathbb{R}^{d_{i}},\, i\geq 2 $$ where $d_i = r_2$, or $r_1+r_2$ depending on the parity of $i$

this can be used to show
- $\operatorname{rank} K_3 =d_2 = r_2$
- $\operatorname{rank} K_5=d_3 = r_1+r_2$
- $\operatorname{rank} K_7=d_4 = r_2$
the covolume of the image under this regulator is a non-zero multiple of $\zeta$

Zagier, Bloch, Suslin

The Bloch-Wigner dilogarithm $D(z)$ can be used to define a map from $\mathcal{B}(\mathbb{C})$ to $\mathbb{R}$.
For $\xi=\sum_{i} n_i[x_i] \in \mathcal{B}(\mathbb{C})$, let $D(\xi)=\sum_{i} n_i D(x_i)$.
by the 5-term relation satisfied by $D$, it is well-defined
For an embedding $\sigma : F\hookrightarrow \mathbb{C}$ and $\xi \in \mathcal{B}(F)$, we may consider $D\left(\sigma(\xi)\right)$.
If $D\left(\sigma(\xi)\right)=0$ for all such embeddings $\sigma$, then $\xi \in \mathcal{B}(F)$ is a torsion element in $\mathcal{B}(F)$.
this is compatible with Borel's regulator

\[ \frac{|d_{K}|^{1/2}}{\pi^{2(r_1 + r_2)}} \zeta_{K}(2) \sim_{\mathbb{Q^{\times}}} \det\left(D(\sigma_i(\xi_j))\right)_{1\leq i,j\leq r_2} \] where $\xi_i,(i=1,\cdots, r_2)$ is $\mathbb{Q}$-basis of $\mathcal{B}(K)\otimes \mathbb{Q}$ and $a\sim_{\mathbb{Q^{\times}}} b$ means $a/b\in\mathbb{Q}$

hyperbolic 3-manifold

집합 $\{0,1,\infty,y,xy\}$ 에서 4개의 원소를 뽑아 얻어지는 교차비(cross ratio)

memo

다른게 아니라 저랑 강원대 강순이 박사님이랑 최근에 Zagier 교수님 쓰신 dilogarithm 논문에 관심이 생겼는데 quantum dilogarithm을 포함해서 자기에 교수님 논문 내용을 강연해줄 수 있는지 부탁드리고자 편지드려요.
Bloc 그룹도 강의해줄 수 있으면 더 좋지만, 아니면 남 추측 관련해서 공부했던 내용이라도 강의해주면 많은 도움이 될 것 같아요.
자기에 교수님 dilogarithm 논문을 읽는데, 부끄럽지만 무슨 말인지 전혀 모르겠더라고요.
q가 나오는 부분과 점근식 부분은 그래도 알겠는데, 나머지 부분들은 능력 밖이라 도움 받을 수 있나해서 여쭤본 겁니다.
그러니까 Bloc 그룹도 이 논문에 나오는 정도 이해할 수 있으면 저는 만족이에요.
quantum dilogarithm 쪽으로 무언가 더 해볼 여지가 있는지 궁금해서 우선 자기에 교수님 논문부터 시작해보려고 했었는데, 시작부터 어렵네요

Bloch-Suslin

$B(\mathbb{F})\simeq K_3^{\operatorname{ind}}(\mathbb{F})$ ??
$0\to \tilde{\mu_{F}}\to K_3^{\operatorname{ind}}(\mathbb{F}) \to B(\mathbb{F})\to 0$ where $0\to \mathbb{Z}/\mathbb{Z}_2 \to \tilde{\mu_{F}} \to \mu_{F}\to 0$ where \mu_{F} is the unit group of F
$K_3^{\operatorname{ind}}(\mathbb{F})$ is a quotient of Milnor K3 by something else

functional equation of $\zeta_K$ implies

$$ \pi^{-d_m} \lim_{s\to -m}\frac{\zeta_K(-m)}{(s+m)^{d_m}} \sim_{\mathbb{Q}^{\times}}\pi ^{-(m+1)(r_1+2 r_2)} \zeta _K(m+1)\left| d_K\right| {}^{\frac{1}{2}} $$ where $d_1 =d_3=\dots = r_2$ or $d_2=d_4=\dots =r_1+r_2$