임시

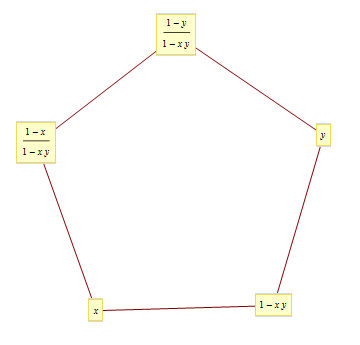
five-term relation

• sequence defined recurrence

\[1-x_{i}=x_{i-1}x_{i+1},\, x_0=x,\, x_2=y\]

• solution

\[x_0=x, x_1=1-xy, x_2=y, x_3=\frac{1-y}{1-xy}, x_4=\frac{1-x}{1-xy}, x_5=x,x_6=1-xy,\dots\]

• 5-periodic

• if \(0<x<1,\,0<y<1\), then \(0<x_i<1\) for all \(i\)
• if \(x=a/(1+a),y = b/(1+b)\), then \(x_0=\frac{a}{a+1},x_1\frac{a+b+1}{ab+a+b+1},\frac{b}{b+1},\frac{a+1}{a+b+1},\frac{b+1}{a+b+1},\dots\)

\( \newcommand{\vol}{\operatorname{vol}} \)

dilogarithm fuction

• Define

\[\operatorname{Li}_ 2(z)= \sum_{n=1}^\infty {z^n \over n^2},\, |z|<1\]

• extend domain

\[\operatorname{Li}_ 2(z) = -\int_0^z{{\log (1-t)}\over t} dt,\, z\in \mathbb C\backslash [1,\infty) \]

functional equations

five-term relation

\[\mbox{Li}_ 2(x)+\mbox{Li}_ 2(y)+\mbox{Li}_ 2 \left( \frac{1-x}{1-xy} \right)+\mbox{Li}_ 2(1-xy)+\mbox{Li}_ 2 \left( \frac{1-y}{1-xy} \right)=\text{elementary}\]

Let us state this in terms of the Rogers dilogarithm (no worry about the branches) \[L(x): =\operatorname{Li}_ 2(x)+\frac{1}{2}\log x\log (1-x)=-\frac{1}{2}\int_{0}^{x}\left(\frac{\log(y)}{1-y}+\frac{\log(1-y)}{y}\right)dy,\, x\in (0,1)\] with \(L(0)=0,\, L(1)=\pi^2/6\)

• \(0< x,y< 1\)

\[L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)=\frac{\pi^2}{2}\]

proof

Let us show that the partial derivatives of \(F(x,y):=L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)\) are 0. Note \[ \frac{d}{dx}L(h(x)) = \frac{1}{2}[\frac{-h'(x) \log (h(x))}{(1-h(x))}-\frac{h'(x) \log (1-h(x))}{h(x)}]. \]

\[ \begin{aligned} 2F_x = & \left(-\frac{\log (x)}{1-x}-\frac{\log (1-x)}{x}\right)+\left(\frac{\log (1-x y)}{x}+\frac{y \log (x y)}{1-x y}\right)+0 \\ & -\frac{(1-y) \log \left(\frac{1-y}{1-x y}\right)+(1-x) y \log \left(\frac{(1-x) y}{1-x y}\right)}{(1-x) (1-x y)} +\frac{(1-x) \log \left(\frac{1-x}{1-x y}\right)+x (1-y) \log \left(\frac{x (1-y)}{1-x y}\right)}{(1-x) x (1-x y)} \\ & =\log (x)\left(\frac{-1}{1-x}+\frac{y}{1-xy}+\frac{(1-y)}{(1-x) (1-x y)} \right)+\dots \\ & =0 \end{aligned} \] Do the same to show \(F_y=0\).

\(\exists\) more intelligent way to control cancellations

Observe \[\frac{d}{dx}L(h(x))=\frac{1}{2}[\log(h(x))\frac{d}{dx}\log (1-h(x))-\log(1-h(x))\frac{d}{dx}\log h(x)]\]

For \(f,g\in \mathbb{Q}(x,y)^{\times}\), define formally \[ f\wedge g : = \frac{1}{2}[\log (f) d (\log (g))-\log (g) d (\log (f))] \] where \(df = f_x dx + f_y dy\).

Then

• \(f\wedge g=-g \wedge f\)
• \((f_1f_2)\wedge g=f_1\wedge g+f_2\wedge g\)

For example, \[dL(h(x,y))=h\wedge (1-h)\]

So \[ dF = F_x dx+F_y dy =x\wedge (1-x)+(1-x y)\wedge (x y)+y\wedge (1-y)+\frac{1-y}{1-x y}\wedge \left(\frac{y(1-x)}{1-x y}\right)+\frac{1-x}{1-x y}\wedge \left(\frac{x(1-y)}{1-xy}\right) =0 \]