오일러의 오각수정리(pentagonal number theorem)

개요

• 오일러의 오각수정리

\[\prod_{n=1}^\infty (1-x^n)=\sum_{k=-\infty}^\infty(-1)^kx^{k(3k-1)/2}\]\[(1-x)(1-x^2)(1-x^3) \cdots = 1 - x - x^2 + x^5 + x^7 - x^{12} - x^{15} + x^{22} + x^{26} + \cdots\]

• 세타함수의 무한곱표현의 일종으로 이해할 수 있음(자코비 세타함수의 삼중곱 공식 참조) \[\sum _{m=-\infty }^{\infty } (-1)^mq^{\frac{3}{2}m^2\pm \frac{1}{2}m} = \prod _{n=1}^{\infty } \left(1-q^{3 n}\right)\left(1-q^{3n-2}\right)\left(1-q^{3n-1}\right)\]
• 자연수의 분할수(integer partitions)\(p(n)\)의 생성함수의 역이다

\[\sum_{n=0}^\infty p(n)x^n = \prod_{n=1}^\infty \frac {1}{1-x^n} = \prod_{n=1}^\infty (1-x^n)^{-1} \]

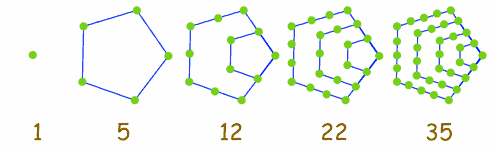
오각수

• 수열 1, 5, 12, 22, 35,...
• 일반항은 \(n(3n-1)/2\)

일반화된 오각수

• \((1-x)(1-x^2)(1-x^3) \cdots = 1 - x - x^2 + x^5 + x^7 - x^{12} - x^{15} + x^{22} + x^{26} + \cdots\)에 등장하는 수
• \(k=\frac{j(3j\pm 1)}{2}\) 꼴로 주어짐 (\(j=1,2,3\cdots\))

증명

• 자코비 세타함수의 삼중곱표현의 특수한 경우로 얻어진다
• 삼중곱에 대해서는 자코비 세타함수 항목 참조

(증명)

\(\prod_{m=1}^\infty \left( 1 - q^{2m}\right) \left( 1 + zq^{2m-1}\right) \left( 1 + z^{-1}q^{2m-1}\right)=\sum_{n=-\infty}^\infty z^{n}q^{n^2}\)

\(q=x^{3/2}\), \(z=-x^{1/2}\)로 두면, 다음을 얻는다 \[\operatorname{(LHS)}=\prod_{m=1}^\infty \left( 1 - x^{3m}\right) \left( 1 - x^{1/2}x^{3m-3/2}\right) \left(1 - x^{-1/2}x^{3m-3/2}\right)=\prod_{m=1}^\infty \left( 1 - x^{3m}\right) \left(1- x^{3m-1}\right) \left(1 - x^{3m-2}\right) = \prod_{n=1}^\infty (1-x^n) \]

\(\operatorname{(RHS)}=\sum_{n=-\infty}^\infty (-1)^{n}x^{n(3n-1)/2}\)■

데데킨트 에타함수

• 위의 급수에 \(q^{1/24}\)를 곱하면, 데데킨트 에타함수의 세타함수 표현을 얻는다 \[\eta(\tau) = q^{1/24} \prod_{n=1}^{\infty} (1-q^{n})=\sum_{n=-\infty}^\infty(-1)^n q^{\frac{(6n+1)^2}{24}}\] 여기서 \(q=e^{2\pi i\tau}\).
• 데데킨트 에타함수는 모듈라 성질을 가진다

역사

• 수학사 연표

관련된 항목들

• 자연수의 분할수(integer partitions)
• 자코비 세타함수
• 정오각형

사전 형태의 자료

• http://ko.wikipedia.org/wiki/오각수
• http://en.wikipedia.org/wiki/pentagonal_number_theorem
• http://en.wikipedia.org/wiki/Pentagonal_numbers

매스매티카 파일 및 계산 리소스

• https://docs.google.com/leaf?id=0B8XXo8Tve1cxZDljNjU2YzYtYjZiNi00ZmVjLWI2NGEtNDBlMmQ0OWY3ZmIy&sort=name&layout=list&num=50
• http://www.wolframalpha.com/input/?i=pentagonal+numbers
• The On-Line Encyclopedia of Integer Sequences
  • A000326, 오각수
  • http://www.research.att.com/~njas/sequences/?q=pentagonal

리뷰논문, 에세이, 강의노트

• Jordan Bell Euler and the pentagonal number theorem, arXiv.org, 2005
• George E. Andrews Euler's Pentagonal Number Theorem, Mathematics Magazine, Vol. 56, No. 5 (Nov., 1983), pp. 279-284

메타데이터

위키데이터

• ID : Q282649

Spacy 패턴 목록

• [{'LOWER': 'pentagonal'}, {'LOWER': 'number'}, {'LEMMA': 'theorem'}]