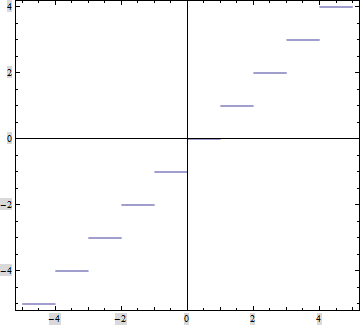
최대정수함수 (가우스함수)

수학노트
둘러보기로 가기 검색하러 가기

개요

  • 실수 x 에 대하여 \(\lfloor x\rfloor\)는 \(x\) 이하의 최대정수를 의미한다

최대정수함수 (가우스함수)2.png

  • 예 \(\lfloor 0.8\rfloor=0\), \(\lfloor -0.2\rfloor=-1\)



에르미트 항등식

  • 실수 \(x\) 와 자연수 \(n\)에 대하여, 다음이 성립한다

\[\sum_{k=0}^{n-1}\left\lfloor x+\frac{k}{n}\right\rfloor=\lfloor nx\rfloor\]


이차잉여에의 응용

  • 서로 소인 두 홀수 \(p,q>0\) 에 대하여 다음이 성립한다

\[\sum_{i=1}^{(p-1)/2}[\frac{iq}{p}]+\sum_{j=1}^{(q-1)/2}[\frac{jp}{q}]=\frac{(p-1)(q-1)}{4}\]



메모

  • \([x]+[x+1/n]+......[x+n-1/n] = [nx]\)


관련된 항목들



사전 형태의 자료

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'floor'}, {'LOWER': 'and'}, {'LOWER': 'ceiling'}, {'LEMMA': 'function'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=최대정수함수_(가우스함수)&oldid=52482"