"포락선(envelope)과 curve stitching"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| 5번째 줄: | 5번째 줄: | ||
* 이러한 그림을 그리는 기술은 curve stitching 또는 string art 라는 이름으로 불리기도 함 | * 이러한 그림을 그리는 기술은 curve stitching 또는 string art 라는 이름으로 불리기도 함 | ||
| − | |||
| − | |||
==포락선(envelope )== | ==포락선(envelope )== | ||
| 17번째 줄: | 15번째 줄: | ||
| − | + | ===증명=== | |
포락선이 <math>\mathbf{r}(t)=(x(t),y(t))</math> 로 매개화되었다고 하자. <math>F(x(t),y(t),t)=0</math>가 성립한다. | 포락선이 <math>\mathbf{r}(t)=(x(t),y(t))</math> 로 매개화되었다고 하자. <math>F(x(t),y(t),t)=0</math>가 성립한다. | ||
| 41번째 줄: | 39번째 줄: | ||
을 만족시킨다. ■ | 을 만족시킨다. ■ | ||
| − | |||
| − | |||
==예1== | ==예1== | ||
| 71번째 줄: | 67번째 줄: | ||
* 이는 [[애스트로이드 (astroid)]] 가 된다 | * 이는 [[애스트로이드 (astroid)]] 가 된다 | ||
[[파일:9431928-_envelope_curve_stitching2.gif]] | [[파일:9431928-_envelope_curve_stitching2.gif]] | ||
| − | |||
| − | |||
| − | |||
| 130번째 줄: | 123번째 줄: | ||
* https://docs.google.com/leaf?id=0B8XXo8Tve1cxZmVkZjZhYTItYjhlNi00ZDA4LWE4OTItMDQyMjU5Yjk5ZWMz&sort=name&layout=list&num=50 | * https://docs.google.com/leaf?id=0B8XXo8Tve1cxZmVkZjZhYTItYjhlNi00ZDA4LWE4OTItMDQyMjU5Yjk5ZWMz&sort=name&layout=list&num=50 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| 146번째 줄: | 132번째 줄: | ||
** envelope - 포락선 | ** envelope - 포락선 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
2013년 5월 23일 (목) 12:58 판
개요
- "one-parameter family 에 있는 모든 곡선에 적어도 한 점에서 접하는 성질을 갖는" 곡선
- 이를 주어진 곡선의 family에 대한 포락선이라 부른다.
- 이러한 그림을 그리는 기술은 curve stitching 또는 string art 라는 이름으로 불리기도 함
포락선(envelope )
- 곡선들이 매개변수 t 에 의해 \(F(x,y,t)=0\) 로 주어진다고 가정하자.
- 이 곡선들에 대한 포락선은 다음 연립방정식에서 t를 소거하여 얻을 수 있다.
\[\left\{ \begin{array}{c} F(x,y,t)=0 \\ \frac{\partial F}{\partial t}(x,y,t)=0 \end{array} \right.\]
증명
포락선이 \(\mathbf{r}(t)=(x(t),y(t))\) 로 매개화되었다고 하자. \(F(x(t),y(t),t)=0\)가 성립한다.
주어진 \(t=t_0\)에 대하여, 포락선의 점은 \(\mathbf{r}'(t_0)=(x(t_0),y(t_0))\) 로 주어진다.
한편 점 \((x(t_0),y(t_0))\)에서, family의 곡선 \(F(x,y,t_0)=0\)에 대하여 \(\mathbf{n}(t_0)=\langle F_{x}(x(t_0),y(t_0),t_0),F_{y}(x(t_0),y(t_0),t_0) \rangle\)는 수직인 벡터가 된다.
따라서 \(\mathbf{r}'(t_0)=\langle x'(t_0),y'(t_0)\rangle\) 에 대하여 \(\mathbf{n}(t_0)\cdot \mathbf{r}'(t_0)=F_{x}(x(t_0),y(t_0),t_0)x'(t_0)+F_{y}(x(t_0),y(t_0),t_0)y'(t_0)=0\)이 성립한다.
\(F(x(t),y(t),t)=0\) 의 양변을 t로 미분하면,
\(F_{x}(x(t_0),y(t_0),t_0)x'(t_0)+F_{y}(x(t_0),y(t_0),t_0)y'(t_0)+F_t(x(t_0),y(t_0),t_0)=0\) 이므로, \(F_t(x(t_0),y(t_0),t_0)=0\)가 성립한다.
임의의 \(t=t_0\)에 대하여 성립하므로, 포락선의 매개방정식 \(\mathbf{r}(t)=(x(t),y(t))\)은 연립방정식
\(\left\{ \begin{array}{c} F(x(t),y(t),t)=0 \\\frac{\partial F}{\partial t}(x(t),y(t),t)=0 \end{array} \right.\)
을 만족시킨다. ■
예1
- 파라메터 t에 대하여 다음과 같은 직선들을 생각하자\[\frac{x}{t}+\frac{y}{10-t}=1\quad, t=1,\cdots, 9\]
- 그림을 보면, 이 직선들에 접하는 곡선이 나타나는 것을 관찰할 수 있다.
- 포락선을 구하기 위해 위에서 언급한 결과를 이용하자\[F(x,y,t)=t^2 + t(y-x-10) + 10x\]\[\frac{\partial F(x,y,t)}{\partial t}=2t+ y-x-10\]
- 따라서 envelope은 다음 두 방정식에서 t를 소거함으로써 얻을 수 있다.
\[\left\{ \begin{array}{c} t^2 + t(y-x-10) + 10x=0 \\ 2t+ y-x-10=0 \end{array} \right.\]
- 이로부터 \(x^2-2 x y-20 x+y^2-20 y+100=0\) 를 얻는다.
- 이는 이차곡선(원뿔곡선) 으로 판별식 \(\Delta=b^2-4ac=4-4=0\) 인, 포물선이 된다.
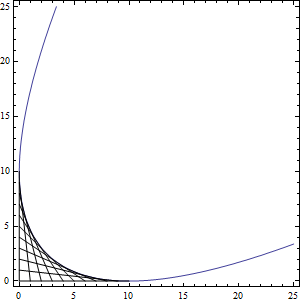
예2: 어떤 타원들의 envelope
- 파라메터 \(0<t<1\)에 대하여 다음과 같은 타원들이 주어진다고 하자\[\frac{x^2}{t^2}+\frac{y^2}{(1-t)^2}=1\]
- \(F(x,y,t)=(t-1)^2 (t-x) (t+x)-t^2 y^2\)
- \(F_{t}(x,y,t)=-2 \left(2 t^3-3 t^2-t x^2-t y^2+t+x^2\right)\)
- \(\left\{ \begin{array}{c} F(x,y,t)=0 \\ \frac{\partial F}{\partial t}(x,y,t)=0 \end{array} \right.\) 으로부터 다음의 두 관계식을 얻을 수 있다
\[\left\{ \begin{array}{c} y^2=(1-t)^3 \\ x^2=t^3 \end{array} \right.\]
- t를 소거하면 \(x^{2/3}+y^{2/3}=1\) 를 얻는다.
- 이는 애스트로이드 (astroid) 가 된다
심장형 곡선
역사
메모
- http://playingwithmathematica.com/2011/04/27/curve-stitching-with-mathematica/
- http://britton.disted.camosun.bc.ca/string_art/jbstringart.htm
- http://www.wikihow.com/Create-a-Line-Design
- 베지에 곡선
- http://en.wikipedia.org/wiki/B%C3%A9zier_curve#Quadratic_curves
- 예
- parabolic line construction
- http://demonstrations.wolfram.com/CircleChordEnvelope/
- envelope
- http://en.wikipedia.org/wiki/Envelope_(mathematics)
- http://jwilson.coe.uga.edu/Texts.Folder/Envel/envelopes.html
- envelope equation
- http://www.sjsu.edu/faculty/watkins/envelopetheo.htm
- Envelopes and String Art (Gregory Quenell) http://faculty.plattsburgh.edu/gregory.quenell/pubpdf/stringart.pdf
관련된 항목들
매스매티카 파일 및 계산 리소스
수학용어번역
- envelope - 대한수학회 수학용어집
- envelope - 포락선


