"A4 종이와 루트2"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
 
(같은 사용자의 중간 판 3개는 보이지 않습니다)
2번째 줄: 2번째 줄:
  
 
* A4 종이의 사이즈는 mm 으로  210 × 297
 
* A4 종이의 사이즈는 mm 으로  210 × 297
−
* 가로세로의 비율:<math>\frac{297}{210}=1.41428\cdots</math><br>
+
* 가로세로의 비율:<math>\frac{297}{210}=1.41428\cdots</math>
 
* 루트 2의 값 <math>\sqrt{2}=1.41421\cdots</math>에 가깝다
 
* 루트 2의 값 <math>\sqrt{2}=1.41421\cdots</math>에 가깝다
  
9번째 줄: 9번째 줄:
 
* A-계열의 종이는 다음과 같은 방식으로 생산됨.
 
* A-계열의 종이는 다음과 같은 방식으로 생산됨.
 
**http://en.wikipedia.org/wiki/File:A_size_illustration.png
 
**http://en.wikipedia.org/wiki/File:A_size_illustration.png
 +
[[파일:2002736-439px-A size illustration2.svg.png]]
 
* 가장 큰 사이즈인 A0를 반으로 자르면 A1두 장.
 
* 가장 큰 사이즈인 A0를 반으로 자르면 A1두 장.
 
* 그 다음 A1을 반으로 자르면 A2 두 장.
 
* 그 다음 A1을 반으로 자르면 A2 두 장.
57번째 줄: 58번째 줄:
 
==블로그==
 
==블로그==
  
−
* [http://bomber0.byus.net/index.php/2007/07/17/422 A4 와 루트2]<br>
+
* [http://bomber0.byus.net/index.php/2007/07/17/422 A4 와 루트2]
 
** 피타고라스의 창, 2007-7-17
 
** 피타고라스의 창, 2007-7-17
 
[[분류:중학수학]]
 
[[분류:중학수학]]
 
[[분류:교양수학]]
 
[[분류:교양수학]]
 +
 +
==메타데이터==
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q1196501 Q1196501]
 +
===Spacy 패턴 목록===
 +
* [{'LEMMA': 'file'}]

2021년 2월 17일 (수) 04:46 기준 최신판

개요

  • A4 종이의 사이즈는 mm 으로 210 × 297
  • 가로세로의 비율\[\frac{297}{210}=1.41428\cdots\]
  • 루트 2의 값 \(\sqrt{2}=1.41421\cdots\)에 가깝다


설명

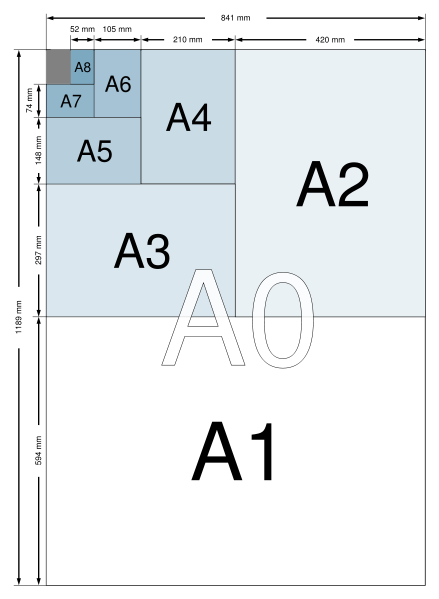
2002736-439px-A size illustration2.svg.png

  • 가장 큰 사이즈인 A0를 반으로 자르면 A1두 장.
  • 그 다음 A1을 반으로 자르면 A2 두 장.
  • 다른 사이즈도 이 과정을 반복해서 얻어지게 됨.
  • 포인트는 이 과정에서 만들어지는 모든 종이의 너비와 길이의 비가 루트 2 라는 것.
  • A0 종이의 세로가 x, 가로가 1의 비율이라면, 다음과 같은 방정식이 만족되어야 함.

\[x:1=1:\frac{x}{2}\] 따라서 \[x=\sqrt{2}\]

  • 이로 인한 장점은 다른 크기의 A-계열 종이 사이에서 원래 모양의 왜곡없이 같은 비율로 확대, 축소 복사가 가능해진다는 것.
  • 큰 종이를 반으로 쩍쩍 갈라대기만 하면 되므로 공정도 단순해짐.
  • 이런 성질은 루트 2말고는 없음.
  • 루트 2는 이런 측면에서 실생활에서 유용한 숫자.



관련된 단원

  • 무리수


관련된 항목들



관련도서

관련된 고교수학 또는 대학수학

  • 귀류법


블로그

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LEMMA': 'file'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=A4_종이와_루트2&oldid=52116"