"구면기하학"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| 1번째 줄: | 1번째 줄: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==개요== | ==개요== | ||
| 30번째 줄: | 22번째 줄: | ||
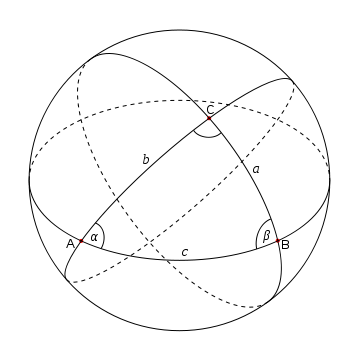
평면상의 직선이 무엇인지는 다들 잘 알고 계실 겁니다. 평면 위의 기하학이 바로 평면기하학, 유클리드 기하학인 것이죠. 그렇다면 구면상에서의 직선은 무엇인가? 구면상에서의 직선은 바로 구면상에 있는 대원들이 됩니다. 구면 위에 두 점이 있을 때, 그 두점과 구의 중심은 하나의 평면을 결정하고, 그 평면과 구면이 만나서 그리는 원을 대원이라고 하는 것이죠. 구면위의 두 점을 지나는 최단곡선은 그렇게 얻어집니다. | 평면상의 직선이 무엇인지는 다들 잘 알고 계실 겁니다. 평면 위의 기하학이 바로 평면기하학, 유클리드 기하학인 것이죠. 그렇다면 구면상에서의 직선은 무엇인가? 구면상에서의 직선은 바로 구면상에 있는 대원들이 됩니다. 구면 위에 두 점이 있을 때, 그 두점과 구의 중심은 하나의 평면을 결정하고, 그 평면과 구면이 만나서 그리는 원을 대원이라고 하는 것이죠. 구면위의 두 점을 지나는 최단곡선은 그렇게 얻어집니다. | ||
| − | + | [[파일:356px-RechtwKugeldreieck.svg.png]] | |
문제는 이제 위와 같이 생긴 삼각형 ABC의 넓이를 어떻게 구할수 있는가 하는 것입니다. 편의를 위해 앞으로 구의 반지름은 1이라고 두겠습니다. | 문제는 이제 위와 같이 생긴 삼각형 ABC의 넓이를 어떻게 구할수 있는가 하는 것입니다. 편의를 위해 앞으로 구의 반지름은 1이라고 두겠습니다. | ||
| − | |||
| − | |||
* 손톱모양의 넓이<br> 북극과 남극을 잇는 두 개의 대원이 이루는 손톱모양의 넓이는, 그 둘 사이의 각도에 의해 결정되고, 그 넓이는 다음과 같습니다.<br><br> 대원둘의 각도가 <math>\theta</math>로 주어졌다면, 손톱모양의 넓이는 <math>2\theta</math>가 됩니다.<br> 넓이가 각도에 비례한다는 사실과, 반지름이 1인 구면의 넓이는 <math>4\pi</math>라는 사실을 이용하면 됩니다.<br> | * 손톱모양의 넓이<br> 북극과 남극을 잇는 두 개의 대원이 이루는 손톱모양의 넓이는, 그 둘 사이의 각도에 의해 결정되고, 그 넓이는 다음과 같습니다.<br><br> 대원둘의 각도가 <math>\theta</math>로 주어졌다면, 손톱모양의 넓이는 <math>2\theta</math>가 됩니다.<br> 넓이가 각도에 비례한다는 사실과, 반지름이 1인 구면의 넓이는 <math>4\pi</math>라는 사실을 이용하면 됩니다.<br> | ||
| + | [[파일:26lune.JPG]] | ||
| 45번째 줄: | 36번째 줄: | ||
세 각이 A,B,C 로 주어진 구면삼각형의 넓이는 <math>A+B+C-\pi</math> 이다 | 세 각이 A,B,C 로 주어진 구면삼각형의 넓이는 <math>A+B+C-\pi</math> 이다 | ||
| − | |||
| − | |||
| − | |||
| − | |||
이를 이용하면, 이제 세 각이 A,B,C 로 주어진 구면삼각형의 넓이를 구할 수 있습니다. | 이를 이용하면, 이제 세 각이 A,B,C 로 주어진 구면삼각형의 넓이를 구할 수 있습니다. | ||
| − | |||
| − | |||
(증명) | (증명) | ||
| − | + | [[파일:26sphere.JPG]] | |
위의 그림처럼, 구면삼각형의 한 꼭지점에서 반대편 극에 마주보고 있는 점까지 대원을 잇습니다. 그러면 위에처럼 회색으로 칠한 손톱모양이 세개 얻어지는데요. 그럼 눈을 크게 뜨고 관찰을 해볼까요. | 위의 그림처럼, 구면삼각형의 한 꼭지점에서 반대편 극에 마주보고 있는 점까지 대원을 잇습니다. 그러면 위에처럼 회색으로 칠한 손톱모양이 세개 얻어지는데요. 그럼 눈을 크게 뜨고 관찰을 해볼까요. | ||
| 116번째 줄: | 101번째 줄: | ||
==역사== | ==역사== | ||
| − | + | * 1603 토마스 해리엇(Thomas Harriot)이 구면삼각형의 넓이 공식을 발견<br> | |
| − | * | + | * 1629 Girard가 구면삼각형의 넓이 공식의 증명을 출판<br> |
| − | * | ||
* http://www.google.com/search?hl=en&tbs=tl:1&q=harriot+girard | * http://www.google.com/search?hl=en&tbs=tl:1&q=harriot+girard | ||
* http://www.google.com/search?hl=en&tbs=tl:1&q=spherical+triangle | * http://www.google.com/search?hl=en&tbs=tl:1&q=spherical+triangle | ||
* [[수학사 연표]] | * [[수학사 연표]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==관련된 항목들== | ==관련된 항목들== | ||
| 153번째 줄: | 117번째 줄: | ||
* [[타일링과 테셀레이션|테셀레이션]] | * [[타일링과 테셀레이션|테셀레이션]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==사전형태의 자료== | ==사전형태의 자료== | ||
| 165번째 줄: | 124번째 줄: | ||
* http://en.wikipedia.org/wiki/Thomas_Harriot | * http://en.wikipedia.org/wiki/Thomas_Harriot | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| 186번째 줄: | 129번째 줄: | ||
==블로그== | ==블로그== | ||
| − | * [http://bomber0.byus.net/index.php/2008/09/26/785 구면삼각형의 넓이에 대한 Girard-Harriot의 정리] | + | * [http://bomber0.byus.net/index.php/2008/09/26/785 구면삼각형의 넓이에 대한 Girard-Harriot의 정리], 피타고라스의 창 |
| − | |||
| − | |||
| − | |||
2013년 1월 24일 (목) 03:22 판
개요
- 구면(sphere) 위의 기하학
- 측지선은 대원으로, 평면기하학에서 직선의 역할을 함
- 직선과 직선 밖의 한 점이 주어져 있을 때, 한 점을 지나는 모든 직선은 주어진 직선과 만남. 즉 평행선은 존재하지 않음.
- 세 각이 A,B,C 로 주어진 반지름 1인 구면삼각형의 넓이는 \(A+B+C-\pi\)
구면상의 미분기하학
- 구면(sphere) 항목 참조
구면삼각형의 넓이
평면상의 직선이 무엇인지는 다들 잘 알고 계실 겁니다. 평면 위의 기하학이 바로 평면기하학, 유클리드 기하학인 것이죠. 그렇다면 구면상에서의 직선은 무엇인가? 구면상에서의 직선은 바로 구면상에 있는 대원들이 됩니다. 구면 위에 두 점이 있을 때, 그 두점과 구의 중심은 하나의 평면을 결정하고, 그 평면과 구면이 만나서 그리는 원을 대원이라고 하는 것이죠. 구면위의 두 점을 지나는 최단곡선은 그렇게 얻어집니다.
문제는 이제 위와 같이 생긴 삼각형 ABC의 넓이를 어떻게 구할수 있는가 하는 것입니다. 편의를 위해 앞으로 구의 반지름은 1이라고 두겠습니다.
- 손톱모양의 넓이
북극과 남극을 잇는 두 개의 대원이 이루는 손톱모양의 넓이는, 그 둘 사이의 각도에 의해 결정되고, 그 넓이는 다음과 같습니다.
대원둘의 각도가 \(\theta\)로 주어졌다면, 손톱모양의 넓이는 \(2\theta\)가 됩니다.
넓이가 각도에 비례한다는 사실과, 반지름이 1인 구면의 넓이는 \(4\pi\)라는 사실을 이용하면 됩니다.
(정리)
세 각이 A,B,C 로 주어진 구면삼각형의 넓이는 \(A+B+C-\pi\) 이다
이를 이용하면, 이제 세 각이 A,B,C 로 주어진 구면삼각형의 넓이를 구할 수 있습니다.
(증명)
위의 그림처럼, 구면삼각형의 한 꼭지점에서 반대편 극에 마주보고 있는 점까지 대원을 잇습니다. 그러면 위에처럼 회색으로 칠한 손톱모양이 세개 얻어지는데요. 그럼 눈을 크게 뜨고 관찰을 해볼까요.
이 손톱모양 세개는 정확히 구면의 절반을 덮고 있습니다.
세개의 손톱모양 각각의 넓이는 위에서 본대로 2A,2B,2C 입니다.
따라서 2A+2B+2C - (구면삼각형 ABC의 넓이 x 2 ) = \(2\pi\) (= 구면의 절반의 넓이)
그러므로 구면삼각형 ABC의 넓이는 \(A+B+C-\pi\). ■
- 한편 면적은 언제나 양수이므로, 구면삼각형의 세 각의 합은 180도보다 크다!
- 왜 삼각형의 세 각의 180도가 아닌 것일까? 평행선을 못 그으니까요2012년 10월 31일 (수) 12:50 (PDT)!!!!!
테셀레이션
- 정다면체에 기반한 구면의 테셀레이션, 똑같이 생긴 삼각형들로 채울수 있는 경우
| 구면기하학 | ||
|---|---|---|
| Td | Oh | Ih |
| *332 | *432 | *532 |
| [[]]
|
[[]]
|
[[]]
|
이 표의 그림속에 구면 위에 그려진 삼각형들이 바로 구면삼각형들인데, 예를 들어 가운데 (4 3 2)라는 녀석은 그 삼각형의 세 각이 각각
\(\frac{\pi}{4},\frac{\pi}{3},\frac{\pi}{2}\)
라는 것을 말한다. 이 삼각형의 세각을 더해보면,
\(\frac{\pi}{4}+\frac{\pi}{3}+\frac{\pi}{2}=\frac{13\pi}{12}\)
가 되어 180도 보다 크다는 것을 알 수 있다. 구면기하학에서는 일반적으로 삼각형의 세 각을 더하면 180도보다 크게 된다. 이는 곡률이 양수이기 때문에 나타나는 현상이다.
역사
- 1603 토마스 해리엇(Thomas Harriot)이 구면삼각형의 넓이 공식을 발견
- 1629 Girard가 구면삼각형의 넓이 공식의 증명을 출판
- http://www.google.com/search?hl=en&tbs=tl:1&q=harriot+girard
- http://www.google.com/search?hl=en&tbs=tl:1&q=spherical+triangle
- 수학사 연표
관련된 항목들
사전형태의 자료
- http://ko.wikipedia.org/wiki/구면기하학
- http://en.wikipedia.org/wiki/spherical_geometry
- http://en.wikipedia.org/wiki/Thomas_Harriot
블로그
- 구면삼각형의 넓이에 대한 Girard-Harriot의 정리, 피타고라스의 창