"구면기하학"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
|||
| (사용자 2명의 중간 판 17개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* [[구면(sphere)]] 위의 기하학 | * [[구면(sphere)]] 위의 기하학 | ||
| 13번째 줄: | 5번째 줄: | ||
* 직선과 직선 밖의 한 점이 주어져 있을 때, 한 점을 지나는 모든 직선은 주어진 직선과 만남. 즉 평행선은 존재하지 않음. | * 직선과 직선 밖의 한 점이 주어져 있을 때, 한 점을 지나는 모든 직선은 주어진 직선과 만남. 즉 평행선은 존재하지 않음. | ||
* 세 각이 A,B,C 로 주어진 반지름 1인 구면삼각형의 넓이는 <math>A+B+C-\pi</math> | * 세 각이 A,B,C 로 주어진 반지름 1인 구면삼각형의 넓이는 <math>A+B+C-\pi</math> | ||
| + | * 넓이는 양수가 되어야 하므로, $A+B+C>\pi$, 즉 삼각형의 세 내각의 합은 180보다 크게 됨 | ||
| 18번째 줄: | 11번째 줄: | ||
| − | + | ==구면상의 미분기하학== | |
* [[구면(sphere)]] 항목 참조 | * [[구면(sphere)]] 항목 참조 | ||
| + | ==구면의 측지선== | ||
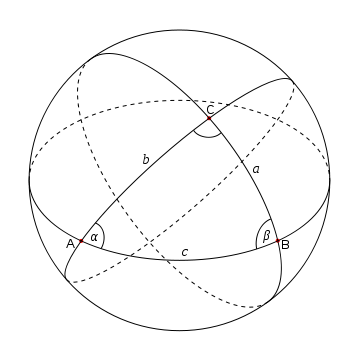
| + | 평면상의 직선이 무엇인지는 다들 잘 알고 계실 겁니다. 평면 위의 기하학이 바로 평면기하학, 유클리드 기하학인 것이죠. 그렇다면 구면상에서의 직선은 무엇인가? 구면상에서의 직선은 바로 구면상에 있는 대원들이 됩니다. 구면 위에 두 점이 있을 때, 그 두점과 구의 중심은 하나의 평면을 결정하고, 그 평면과 구면이 만나서 그리는 원을 대원이라고 하는 것이죠. 구면위의 두 점을 지나는 최단곡선은 그렇게 얻어집니다. | ||
| + | [[파일:356px-RechtwKugeldreieck.svg.png]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | + | ==구면삼각형== |
| + | * 세 각이 A,B,C 로 주어진 구면삼각형의 넓이는 <math>A+B+C-\pi</math> 이다 | ||
| + | * [[구면삼각형]] 항목 참조 | ||
| − | |||
| − | |||
| − | |||
| + | ===삼각형의 세 각의 합=== | ||
* 한편 면적은 언제나 양수이므로, '''구면삼각형의 세 각의 합은 180도보다 크다'''! | * 한편 면적은 언제나 양수이므로, '''구면삼각형의 세 각의 합은 180도보다 크다'''! | ||
| − | * 왜 삼각형의 세 각의 180도가 아닌 것일까? 평행선을 못 그으니까요 | + | * 왜 삼각형의 세 각의 180도가 아닌 것일까? 평행선을 못 그으니까요!!!!! |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| + | ==테셀레이션== | ||
| + | * 정다면체에 기반한 구면의 [[타일링과 테셀레이션|테셀레이션]]은 ( 3 3 2), (4 3 2), (5 3 2) 세 가지가 있다 | ||
| + | * 예를 들어 가운데 (4 3 2)라는 녀석은 그 삼각형의 세 각이 각각 | ||
| + | :<math>\frac{\pi}{4},\frac{\pi}{3},\frac{\pi}{2}</math> | ||
라는 것을 말한다. 이 삼각형의 세각을 더해보면, | 라는 것을 말한다. 이 삼각형의 세각을 더해보면, | ||
| − | + | :<math>\frac{\pi}{4}+\frac{\pi}{3}+\frac{\pi}{2}=\frac{13\pi}{12}</math> | |
| − | <math>\frac{\pi}{4}+\frac{\pi}{3}+\frac{\pi}{2}=\frac{13\pi}{12}</math> | ||
| − | |||
가 되어 180도 보다 크다는 것을 알 수 있다. '''구면기하학에서는 일반적으로 삼각형의 세 각을 더하면 180도보다 크게 된다.''' 이는 곡률이 양수이기 때문에 나타나는 현상이다. | 가 되어 180도 보다 크다는 것을 알 수 있다. '''구면기하학에서는 일반적으로 삼각형의 세 각을 더하면 180도보다 크게 된다.''' 이는 곡률이 양수이기 때문에 나타나는 현상이다. | ||
| − | + | ==메모== | |
| − | + | * http://latexblue.mechanicalmischief.com/SphericalAngles.html | |
| − | + | * pole-polar duality | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * http:// | ||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==역사== | |
| + | * 1603 토마스 해리엇(Thomas Harriot)이 구면삼각형의 넓이 공식을 발견 | ||
| + | * 1629 Girard가 구면삼각형의 넓이 공식의 증명을 출판 | ||
| + | * [[수학사 연표]] | ||
| − | |||
| − | + | ==관련된 항목들== | |
| − | + | * [[구면삼각법]] | |
| − | |||
* [[가우스-보네 정리]] | * [[가우스-보네 정리]] | ||
* [[다면체에 대한 오일러의 정리 V-E+F=2]] | * [[다면체에 대한 오일러의 정리 V-E+F=2]] | ||
| 147번째 줄: | 65번째 줄: | ||
* [[타일링과 테셀레이션|테셀레이션]] | * [[타일링과 테셀레이션|테셀레이션]] | ||
| − | |||
| − | + | ==매스매티카 파일 및 계산 리소스== | |
| + | * https://docs.google.com/file/d/0B8XXo8Tve1cxQnFTZHNoUmFfVkU/edit | ||
| + | * [http://merganser.math.gvsu.edu/easel/ Spherical Easel A spherical drawing program] | ||
| + | * [http://demonstrations.wolfram.com/SphericalTriangleSolutions/ Spherical Triangle Solutions] | ||
| + | * [http://demonstrations.wolfram.com/DigonTilingOfAHosohedron/ Digon Tiling of a Hosohedron] | ||
| − | |||
| − | + | ==사전형태의 자료== | |
| − | * | + | * http://ko.wikipedia.org/wiki/구면기하학 |
* http://en.wikipedia.org/wiki/spherical_geometry | * http://en.wikipedia.org/wiki/spherical_geometry | ||
| + | * http://en.wikipedia.org/wiki/Thomas_Harriot | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==리뷰, 에세이, 강의노트== | |
| + | * Papadopoulos, Athanase. “On the Works of Euler and His Followers on Spherical Geometry.” arXiv:1409.4736 [math], September 16, 2014. http://arxiv.org/abs/1409.4736. | ||
| − | + | [[분류:구면기하학]] | |
| − | |||
| − | |||
| − | |||
2014년 9월 16일 (화) 19:49 판
개요
- 구면(sphere) 위의 기하학
- 측지선은 대원으로, 평면기하학에서 직선의 역할을 함
- 직선과 직선 밖의 한 점이 주어져 있을 때, 한 점을 지나는 모든 직선은 주어진 직선과 만남. 즉 평행선은 존재하지 않음.
- 세 각이 A,B,C 로 주어진 반지름 1인 구면삼각형의 넓이는 \(A+B+C-\pi\)
- 넓이는 양수가 되어야 하므로, $A+B+C>\pi$, 즉 삼각형의 세 내각의 합은 180보다 크게 됨
구면상의 미분기하학
- 구면(sphere) 항목 참조
구면의 측지선
평면상의 직선이 무엇인지는 다들 잘 알고 계실 겁니다. 평면 위의 기하학이 바로 평면기하학, 유클리드 기하학인 것이죠. 그렇다면 구면상에서의 직선은 무엇인가? 구면상에서의 직선은 바로 구면상에 있는 대원들이 됩니다. 구면 위에 두 점이 있을 때, 그 두점과 구의 중심은 하나의 평면을 결정하고, 그 평면과 구면이 만나서 그리는 원을 대원이라고 하는 것이죠. 구면위의 두 점을 지나는 최단곡선은 그렇게 얻어집니다.
구면삼각형
- 세 각이 A,B,C 로 주어진 구면삼각형의 넓이는 \(A+B+C-\pi\) 이다
- 구면삼각형 항목 참조
삼각형의 세 각의 합
- 한편 면적은 언제나 양수이므로, 구면삼각형의 세 각의 합은 180도보다 크다!
- 왜 삼각형의 세 각의 180도가 아닌 것일까? 평행선을 못 그으니까요!!!!!
테셀레이션
- 정다면체에 기반한 구면의 테셀레이션은 ( 3 3 2), (4 3 2), (5 3 2) 세 가지가 있다
- 예를 들어 가운데 (4 3 2)라는 녀석은 그 삼각형의 세 각이 각각
\[\frac{\pi}{4},\frac{\pi}{3},\frac{\pi}{2}\] 라는 것을 말한다. 이 삼각형의 세각을 더해보면, \[\frac{\pi}{4}+\frac{\pi}{3}+\frac{\pi}{2}=\frac{13\pi}{12}\] 가 되어 180도 보다 크다는 것을 알 수 있다. 구면기하학에서는 일반적으로 삼각형의 세 각을 더하면 180도보다 크게 된다. 이는 곡률이 양수이기 때문에 나타나는 현상이다.
메모
- http://latexblue.mechanicalmischief.com/SphericalAngles.html
- pole-polar duality
역사
- 1603 토마스 해리엇(Thomas Harriot)이 구면삼각형의 넓이 공식을 발견
- 1629 Girard가 구면삼각형의 넓이 공식의 증명을 출판
- 수학사 연표
관련된 항목들
매스매티카 파일 및 계산 리소스
- https://docs.google.com/file/d/0B8XXo8Tve1cxQnFTZHNoUmFfVkU/edit
- Spherical Easel A spherical drawing program
- Spherical Triangle Solutions
- Digon Tiling of a Hosohedron
사전형태의 자료
- http://ko.wikipedia.org/wiki/구면기하학
- http://en.wikipedia.org/wiki/spherical_geometry
- http://en.wikipedia.org/wiki/Thomas_Harriot
리뷰, 에세이, 강의노트
- Papadopoulos, Athanase. “On the Works of Euler and His Followers on Spherical Geometry.” arXiv:1409.4736 [math], September 16, 2014. http://arxiv.org/abs/1409.4736.