구면기하학

The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.

개요

구면(sphere) 위의 기하학
측지선은 대원으로, 평면기하학에서 직선의 역할을 함
직선과 직선 밖의 한 점이 주어져 있을 때, 한 점을 지나는 모든 직선은 주어진 직선과 만남. 즉 평행선은 존재하지 않음.
세 각이 A,B,C 로 주어진 반지름 1인 구면삼각형의 넓이는 $A+B+C-\pi$
넓이는 양수가 되어야 하므로, $A+B+C>\pi$, 즉 삼각형의 세 내각의 합은 180보다 크게 됨

구면상의 미분기하학

구면(sphere) 항목 참조

구면의 측지선

평면상의 직선이 무엇인지는 다들 잘 알고 계실 겁니다. 평면 위의 기하학이 바로 평면기하학, 유클리드 기하학인 것이죠. 그렇다면 구면상에서의 직선은 무엇인가? 구면상에서의 직선은 바로 구면상에 있는 대원들이 됩니다. 구면 위에 두 점이 있을 때, 그 두점과 구의 중심은 하나의 평면을 결정하고, 그 평면과 구면이 만나서 그리는 원을 대원이라고 하는 것이죠. 구면위의 두 점을 지나는 최단곡선은 그렇게 얻어집니다.

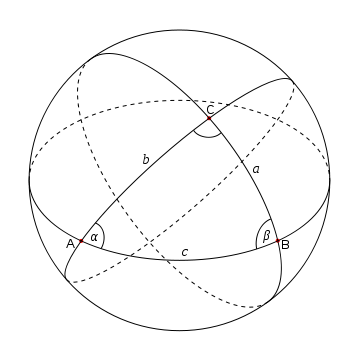
구면삼각형

세 각이 A,B,C 로 주어진 구면삼각형의 넓이는 $A+B+C-\pi$ 이다
구면삼각형 항목 참조

삼각형의 세 각의 합

한편 면적은 언제나 양수이므로, 구면삼각형의 세 각의 합은 180도보다 크다!
왜 삼각형의 세 각의 180도가 아닌 것일까? 평행선을 못 그으니까요!!!!!

테셀레이션

정다면체에 기반한 구면의 테셀레이션은 ( 3 3 2), (4 3 2), (5 3 2) 세 가지가 있다
예를 들어 가운데 (4 3 2)라는 녀석은 그 삼각형의 세 각이 각각

\[\frac{\pi}{4},\frac{\pi}{3},\frac{\pi}{2}\] 라는 것을 말한다. 이 삼각형의 세각을 더해보면, \[\frac{\pi}{4}+\frac{\pi}{3}+\frac{\pi}{2}=\frac{13\pi}{12}\] 가 되어 180도 보다 크다는 것을 알 수 있다. 구면기하학에서는 일반적으로 삼각형의 세 각을 더하면 180도보다 크게 된다. 이는 곡률이 양수이기 때문에 나타나는 현상이다.

메모

http://latexblue.mechanicalmischief.com/SphericalAngles.html
pole-polar duality

역사

1603 토마스 해리엇(Thomas Harriot)이 구면삼각형의 넓이 공식을 발견
1629 Girard가 구면삼각형의 넓이 공식의 증명을 출판
수학사 연표

매스매티카 파일 및 계산 리소스

사전형태의 자료