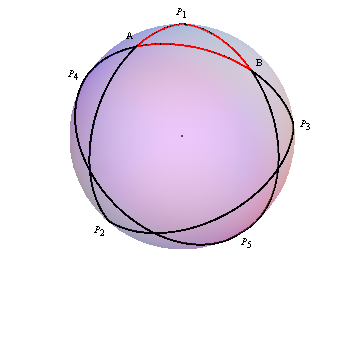
놀라운 펜타그램 (Pentagramma Mirificum)
개요
- 구면 위에 주어진 직각삼각형에서 시작하여 얻어지는 펜타그램
구성
기호
- 구면 위의 점 \(R,S\)
- \(RS\)는 \(R,S\)를 지나는 대원
- \(R'\) : 꼭지점 \(R\)을 극점이라 할 때 적도에 해당하는 대원
- \(C_1\cap C_2\) : 두 대원 \(C_1,C_2\)의 교점
펜타그램의 꼭지점
- 꼭지점 \(P_1\)에서 직각인 구면위의 직각삼각형 \(P_1AB\)
- 구면 위의 꼭지점 \(P_2,\cdots, P_5\)를 다음과 같이 정의
- \(P_2=P_1A\cap A'\)
- \(P_5=P_1B\cap B'\)
- \(P_3=AB\cap A'\)
- \(P_4=BA\cap B'\)
- 펜타그램 \(P_1P_2P_3P_4P_5\)의 각 꼭지점에서 모두 직각
메모
- http://mathcentral.uregina.ca/mp/previous2006/nov06sol.php
- http://www.math.uni-bielefeld.de/~sek/cluster/pentagramma/
- http://math.univ-lyon1.fr/~okra/Claude2009/TALKS/Claude-fest-Tabachnikov.pdf
- http://www.larouchepub.com/eiw/public/2005/2005_40-49/2005-40/pdf/40-49_39_featbruce.pdf
Gauss was intrigued by the relationship of Napier’s spherical pentagram to his elliptical transcendentals. He realized that Napier’s pentagramma mirificum established that a spherical surface had an intrinsic five-fold periodicity. He saw this five-fold periodicity in light of a well known discovery of Apollonius that five points are required to uniquely determine a conic section. This distinguishes the general conic section from a circle, which requires only three points, and a line, that requires only two. Gauss recognized that the five-fold periodicity of the sphere and the five point determination of conics, reflected the distinction between the higher form of elliptical transcendentals and the lower form of transcendental associated with circular, hyperbolic and exponential functions.
관련된 항목들
수학용어번역
매스매티카 파일 및 계산 리소스
- https://docs.google.com/file/d/0B8XXo8Tve1cxVU9saE43ckpGbU0/edit?usp=drivesdk
- Pentagramma Mirificum Geometric Explorations, Ben Deniston
사전 형태의 자료
리뷰, 에세이, 강의노트
- Schwartz, Richard Evan, and Serge Tabachnikov. 2010. “Elementary Surprises in Projective Geometry.” The Mathematical Intelligencer 32 (3): 31–34. doi:10.1007/s00283-010-9137-8.
- Geometric Unfolding of a Difference Equation E. Christopher Zeeman, K.B., F.R.S. UT San Antonio, March 10, 1997 / Trinity University, March 17, 1997
관련논문
- Schechtman, Vadim. 2011. “Pentagramma Mirificum and Elliptic Functions”. ArXiv e-print 1106.3633. http://arxiv.org/abs/1106.3633.
- Coxeter, H. S. M. 1971. “Frieze Patterns.” Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica 18: 297–310. https://eudml.org/doc/204992
- Cayley, Arthur. 2009. “427. On Gauss’ Pentagramma Mirificum.” In The Collected Mathematical Papers. Vol. 7. Cambridge Library Collection - Mathematics. Cambridge University Press. http://dx.doi.org/10.1017/CBO9780511703737.012.
노트
위키데이터
- ID : Q60170081
말뭉치
- These formulas appeared in the paper by Gauss "Pentagramma Mirificum", published posthumously; Gauss cal- culated geometric quantities characterizing spherical self-polar pentagons, see Figure 3 .[1]
- All that is know to this author, are some of Gauss' personal notes respecting his breakthroughs investigating the Pentagramma Mirificum, published in his collected works.[2]
- To fully grasp the significance of the pentagramma it is necessary to discover how to work in a spherical geometry.[2]
- We shall begin with one of a number of methods of construction of the pentagramma mirificum.[2]
- To reach the pentagramma mirificum, begin by constructing an arbitrary spherical right triangle, whose only constraint is that each side is less then 90 degrees.[2]
- According to De Morgan, Torporley anticipated by a dozen years the famous rules of Napier which Gauss embodied in his pentagramma mirificum...[3]
- For a more extensive survey see Coxeter's Frieze patterns at the Crossroads of Algebra, Geometry and Combinatorics by Morier-Genoud, where the pentagramma mirificum is also discussed.[3]
- Pentagramma mirificum (Latin for miraculous pentagram) is a star polygon on a sphere, composed of five great circle arcs, all of whose internal angles are right angles.[4]
소스
노트
위키데이터
- ID : Q60170081
말뭉치
- All that is know to this author, are some of Gauss' personal notes respecting his breakthroughs investigating the Pentagramma Mirificum, published in his collected works.[1]
- To fully grasp the significance of the pentagramma it is necessary to discover how to work in a spherical geometry.[1]
- We shall begin with one of a number of methods of construction of the pentagramma mirificum.[1]
- To reach the pentagramma mirificum, begin by constructing an arbitrary spherical right triangle, whose only constraint is that each side is less then 90 degrees.[1]
- Pentagramma mirificum (Latin for miraculous pentagram) is a star polygon on a sphere, composed of five great circle arcs, all of whose internal angles are right angles.[2]
- These formulas appeared in the paper by Gauss "Pentagramma Mirificum", published posthumously; Gauss cal- culated geometric quantities characterizing spherical self-polar pentagons, see Figure 3 .[3]
- These were associated with a simple 5-fold structure later termed the Pentagramma Mirificum by the mathematician Carl Friedrich Gauss.[4]
- Exploration of the possible relationship between the pattern of Wu Xing, Hygeia and the Pentagramma Mirificum can be usefully related to that of the non-sequiturs of so-called Knight's Move thinking.[4]
- This geometry is remarkably illustrated by the interactive animations of the LaRouche group (Full Circle; The Pentagramma Mirificum).[4]
- The 2-part Pentagramma Mirificum could be considered as indicative of a form of minimal cognitive system to enable global cognitive circumnavigation.[4]
- According to De Morgan, Torporley anticipated by a dozen years the famous rules of Napier which Gauss embodied in his pentagramma mirificum...[5]
- For a more extensive survey see Coxeter's Frieze patterns at the Crossroads of Algebra, Geometry and Combinatorics by Morier-Genoud, where the pentagramma mirificum is also discussed.[5]
- Classical frieze patterns are combinatorial structures which relate back to Gauss' Pentagramma Mirificum, and have been extensively studied by Conway and Coxeter in the 1970's.[6]
- Global Psychosocial Implication in the Pentagramma Mirificum, is included.[7]
- The smallest non-trivial cluster algebra was discussed already by Gauss under the name Pentagramma Mirificum.[8]
- We also provide a noncommutative version of the celebrated "pentagramma mirificum".[9]
소스
- ↑ 1.0 1.1 1.2 1.3 Pentagramma Part 1
- ↑ Pentagramma mirificum
- ↑ Pentagramma mirificum of Carl Friedrich Gauss.
- ↑ 4.0 4.1 4.2 4.3 Global Psychosocial Implication in the Pentagramma Mirificum
- ↑ 5.0 5.1 What are the modern connections of the Pentagramma Mirificum studied by Gauss?
- ↑ Manchester Algebra Seminar - Sira Gratz - SL(k)-friezes
- ↑ Global Psychosocial Implication in the Pentagramma Mirificum
- ↑ Padua: Cluster Theory
- ↑ Noncommutative cross-ratio and Schwarz derivative
메타데이터
위키데이터
- ID : Q60170081
Spacy 패턴 목록
- [{'LOWER': 'pentagramma'}, {'LEMMA': 'mirificum'}]
- [{'LOWER': 'miraculous'}, {'LEMMA': 'pentagram'}]