"로저스 다이로그 함수 (Rogers dilogarithm)"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| 3번째 줄: | 3번째 줄: | ||
* [[다이로그 함수(dilogarithm)]] 의 변종<br> | * [[다이로그 함수(dilogarithm)]] 의 변종<br> | ||
* 다양한 [[함수 다이로그 항등식(functional dilogarithm identity)]] 을 만족시킴<br> | * 다양한 [[함수 다이로그 항등식(functional dilogarithm identity)]] 을 만족시킴<br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| 12번째 줄: | 8번째 줄: | ||
==정의== | ==정의== | ||
| − | * <math>x\in (0,1)</math>에서 로저스 다이로그 함수를 다음과 같이 정의:<math>L(x)=\operatorname{Li}_ 2(x)+\frac{1}{2}\log x\log (1-x)=-\frac{1}{2}\int_{0}^{x}\frac{\log(1-y)}{y}+\frac{\log(y)}{1- | + | * <math>x\in (0,1)</math>에서 로저스 다이로그 함수를 다음과 같이 정의 |
| + | :<math>L(x)=\operatorname{Li}_ 2(x)+\frac{1}{2}\log x\log (1-x)=-\frac{1}{2}\int_{0}^{x}\left(\frac{\log(1-y)}{y}+\frac{\log(y)}{1-yright)dy</math> | ||
* <math>(-\infty,0],[1,+\infty)</math>를 제외한 복소평면으로 해석적확장됨<br> | * <math>(-\infty,0],[1,+\infty)</math>를 제외한 복소평면으로 해석적확장됨<br> | ||
* <math>dL(y)=\frac{1}{2}[\log(y)d\log (1-y)-\log(1-y)d\log (y)]</math><br> | * <math>dL(y)=\frac{1}{2}[\log(y)d\log (1-y)-\log(1-y)d\log (y)]</math><br> | ||
| + | |||
==함수의 그래프== | ==함수의 그래프== | ||
2013년 7월 12일 (금) 13:29 판
개요
- 다이로그 함수(dilogarithm) 의 변종
- 다양한 함수 다이로그 항등식(functional dilogarithm identity) 을 만족시킴
정의
- \(x\in (0,1)\)에서 로저스 다이로그 함수를 다음과 같이 정의
\[L(x)=\operatorname{Li}_ 2(x)+\frac{1}{2}\log x\log (1-x)=-\frac{1}{2}\int_{0}^{x}\left(\frac{\log(1-y)}{y}+\frac{\log(y)}{1-yright)dy\]
- \((-\infty,0],[1,+\infty)\)를 제외한 복소평면으로 해석적확장됨
- \(dL(y)=\frac{1}{2}[\log(y)d\log (1-y)-\log(1-y)d\log (y)]\)
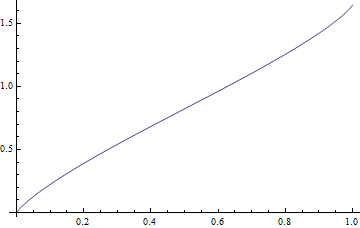
함수의 그래프
- \(x\in (0,1)\) 에서의 그래프
- 함수 방정식을 이용한 확장
반사공식(오일러)
- \(0\leq x \leq 1\) 일 때\[L(x)+L(1-x)=L(1)\]
5항 관계식
- \(0\leq x,y\leq 1\) 일 때, \[L(x)+L(1-xy)+L(y)+L(\frac{1-y}{1-xy})+L\left( \frac{1-x}{1-xy}\right)=\frac{\pi^2}{2}\]
special values
\(L(0)=0\)
\(L(1)=\frac{\pi^2}{6}\)
\(L(-1)=-\frac{\pi^2}{12}\)
\(L(\frac{1}{2})=\frac{\pi^2}{12}\)
\(L(\frac{3-\sqrt{5}}{2})=\frac{\pi^2}{15}\)
\(L(\frac{-1+\sqrt{5}}{2})=\frac{\pi^2}{10}\)
- non-unitary \(c(2,k+2)\) minimal models \[\sum_{i=1}^{[k/2]}L(\frac{\sin^2\frac{\pi}{k+2}}{\sin^2\frac{(i+1)\pi}{k+2}})=\frac{k-1}{k+2}\cdot \frac{\pi^2}{6}\]
역사
메모
관련된 항목들
매스매티카 파일 및 계산 리소스
- https://docs.google.com/leaf?id=0B8XXo8Tve1cxZGMwYzhkZjItMmY5Ny00NDI4LTgxYjktN2E2NDlkNmNjMjAz&sort=name&layout=list&num=50
- http://www.wolframalpha.com/input/?i=
- http://functions.wolfram.com/
- NIST Digital Library of Mathematical Functions
- The On-Line Encyclopedia of Integer Sequences
- Numbers, constants and computation
수학용어번역
사전 형태의 자료
관련논문
- Algebraic Dilogarithm Identities
- Basil Gordon and Richard J. Mcintosh, 1997
- Dilogarithm identities
- Anatol N. Kirillov,Prog.Theor.Phys.Suppl.118:61-142, 1995
- Identities for the Rogers dilogarithm function connected with simple Lie algebras
- A. N. Kirillov, 1989
- http://www.jstor.org/action/doBasicSearch?Query=
- http://dx.doi.org/10.1023/A:1009709927327
관련도서
- Harold Scott Macdonald Coxeter The beauty of geometry: twelve essays
- chapter 1