"뫼비우스 변환"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
|||
| (사용자 2명의 중간 판 26개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | + | * 복소평면 (더 정확히는 리만구면) 상의 복소수를, 또다른 복소수로 보내는 함수 | |
| − | * 복소평면 (더 정확히는 리만구면) 상의 | + | * <math>a,b,c,d\in\Bbb{C} \mbox{ and } ad-bc \ne 0</math>일 때, 뫼비우스 변환은 다음과 같이 주어짐 |
| − | + | : <math>f(z) = \frac{az+b}{cz+d}</math> | |
| − | <math> | + | * 하나의 뫼비우스변환은 <math>GL(2,\mathbb{C})</math>의 원소로 표현되지만, 행렬들의 상수배정도는 모두 똑같은 역할을 하므로, 전체 뫼비우스변환군은 <math>PGL(2,\mathbb{C})</math>와 동형인 군이 됨. |
| − | + | * 겹선형(bilinear) 또는 linear fractional transformation 으로 불리기도 함. | |
| − | + | * 해석함수로 각도와 방향을 보존함. | |
| − | |||
| − | * 하나의 뫼비우스변환은 GL(2,C)의 원소로 표현되지만, 행렬들의 상수배정도는 모두 똑같은 역할을 하므로, | ||
| − | * bilinear 또는 linear fractional transformation | ||
| − | * | ||
* 뫼비우스 변환은 복소평면보다 리만구면에 정의된 변환으로 이해하는 것이 바람직함. | * 뫼비우스 변환은 복소평면보다 리만구면에 정의된 변환으로 이해하는 것이 바람직함. | ||
| − | * 리만구면 = 1차원 복소사영공간 | + | * 리만구면 = 1차원 [[복소사영공간]] |
* 원이나 직선들을 모두 원이나 직선으로 보냄. (직선을 반지름이 무한대인 원으로 생각한다면, 원을 원으로 보냄.) | * 원이나 직선들을 모두 원이나 직선으로 보냄. (직선을 반지름이 무한대인 원으로 생각한다면, 원을 원으로 보냄.) | ||
* [[교차비(cross ratio)|교차비]]를 보존함. | * [[교차비(cross ratio)|교차비]]를 보존함. | ||
| 18번째 줄: | 14번째 줄: | ||
* 리만구에 작용하는 뫼비우스 변환들이 이루는 군의 분류 문제는 많은 수학의 분야와 밀접하게 관련. | * 리만구에 작용하는 뫼비우스 변환들이 이루는 군의 분류 문제는 많은 수학의 분야와 밀접하게 관련. | ||
| − | + | ||
| − | + | ||
| − | + | ==반전 사상과 뫼비우스 변환== | |
| − | * [[ | + | * [[반전 사상(inversion)]] |
| − | * <math>z \mapsto \frac{1}{\bar{z}}</math> | + | * <math>z \mapsto \frac{1}{\bar{z}}</math> 는 복소평면 상에서 고전적인 반전 사상이 된다. 하지만 방향(orientation)을 보존하지 않으므로, 해석함수가 되지 않음. |
| − | * 뫼비우스 변환 <math>z \mapsto \frac{1}{z}</math> | + | * 뫼비우스 변환 <math>z \mapsto \frac{1}{z}</math> 는 고전적인 평면기하의 반전 사상과 복소평면 상에서 x축에 대한 대칭사상의 합성으로, 방향을 보존하게 되고, 해석함수가 됨. |
| − | + | ||
| − | + | ||
| − | + | ==한 점에서의 사영과 뫼비우스 변환== | |
| − | * 두 주어진 | + | * 두 주어진 직선 A,B와 두 직선 밖의 주어진 점 <math>P'</math>가 있다. |
| − | * 직선 | + | * 직선 A 위의 점 <math>P</math>와 <math>P'</math>를 지나는 직선이 직선 B에서 만나는 점을 <math>\pi(P)</math> 라 하자. |
| − | * | + | * <math>\pi :A \to B</math> 를 이와 같이 정의할 수 있다. |
| − | * 직선이 아닌 원에 대해서도 마찬가지로 정의가 가능. | + | * 직선이 아닌 원에 대해서도 마찬가지로 정의가 가능.[[파일:3259985-afigure006-riemann65.jpg]] |
| − | + | ||
| − | + | ||
| − | + | ==뫼비우스 변환과 원과 직선== | |
| − | * 직선의 방정식 | + | * 직선의 방정식 |
| − | ** <math>ax+by+c=0, a,b,c \in \mathbb{R}</math> | + | ** <math>ax+by+c=0, a,b,c \in \mathbb{R}</math> |
** <math>Bz+\bar{B}\bar{z}+c=0, z=x+iy, B=\frac{a}{2}-\frac{ib}{2}</math> | ** <math>Bz+\bar{B}\bar{z}+c=0, z=x+iy, B=\frac{a}{2}-\frac{ib}{2}</math> | ||
| − | ** 두 표현은 같은 | + | ** 두 표현은 같은 직선의 표현 |
| − | * 원의 방정식 | + | * 원의 방정식 |
** <math>|z-z_0|=\rho</math> | ** <math>|z-z_0|=\rho</math> | ||
** <math>z\bar{z}+\bar{B}z+B\bar{z}+c=0, B=-z_0, c=|B|^2-\rho^2</math> | ** <math>z\bar{z}+\bar{B}z+B\bar{z}+c=0, B=-z_0, c=|B|^2-\rho^2</math> | ||
** 두 표현은 같은 원의 표현 | ** 두 표현은 같은 원의 표현 | ||
| − | * | + | * 따라서 <math>az\bar{z}+\bar{B}z+{B}\bar{z}+c=0, a,c\in \mathbb{R}</math> 는 원과 직선의 방정식이 됨. |
* 뫼비우스 변환은 이러한 형태의 식을 보존하므로, 원과 직선을 원과 직선으로 보냄. | * 뫼비우스 변환은 이러한 형태의 식을 보존하므로, 원과 직선을 원과 직선으로 보냄. | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | < | + | ==교차비와 뫼비우스 변환== |
| + | * 뫼비우스 변환이 네 점, <math>z_1,z_2,z_3,z_4</math> 를 <math>w_1,w_2,w_3,w_4</math>로 보내는 경우, 교차비는 보존됨. | ||
| + | :<math>\frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)} = \frac{(w_1-w_3)(w_2-w_4)}{(w_2-w_3)(w_1-w_4)}</math> | ||
| + | * 교차비를 보존하는 복소함수가 네 점 <math>z,z_2,z_3,z_4</math>를 <math>w,1,0,\infty</math>로 보낼 경우, <math>(z,z_2;z_3,z_4) =(w,1;0,\infty)</math> 로부터 다음의 뫼비우스변환을 유도할 수 있음 | ||
| + | :<math>w = \frac{(z-z_3)(z_2-z_4)}{(z_2-z_3)(z-z_4)}</math> | ||
| + | * [[교차비(cross ratio)]] 항목 참조 | ||
| − | |||
| − | |||
| − | + | ==세 점== | |
| − | < | + | * 사영기하학의 관점에서 <math>\{0,1,\infty\}</math>의 선택이 좋은 이유 |
| + | * <math>0</math> 은 기준점의 역할 | ||
| + | * <math>1</math> 은 단위길이를 결정 | ||
| − | + | The first set of fixed points is {0, 1, ∞}. However, the cross-ratio can never take on these values if the points {z<sub style="line-height: 1em;">i</sub>} are all distinct. These values are limit values as one pair of coordinates approach each other: | |
| − | |||
| − | |||
| − | |||
| − | The first set of fixed points is {0, 1, ∞}. However, the cross-ratio can never take on these values if the points {z<sub style=" | ||
: <math>(z,z_2;z,z_4) = (z_1,z;z_3,z) = 0\,</math> | : <math>(z,z_2;z,z_4) = (z_1,z;z_3,z) = 0\,</math> | ||
| 96번째 줄: | 77번째 줄: | ||
: <math>(z,z_2;z_3,z) = (z_1,z;z,z_4) = \infty.</math> | : <math>(z,z_2;z_3,z) = (z_1,z;z,z_4) = \infty.</math> | ||
| − | + | ||
| − | |||
| − | |||
| − | + | ||
| − | * Cross ratio | + | ==메모== |
| + | * 사영기하학과 뫼비우스 변환 | ||
| + | * Cross ratio | ||
** central projection and cross ratio | ** central projection and cross ratio | ||
** inversion and cross ratio | ** inversion and cross ratio | ||
| − | |||
| − | |||
* Steiner's theorem | * Steiner's theorem | ||
| − | + | ||
| − | + | ||
| − | + | ==관련된 고교수학 또는 대학수학== | |
| − | |||
| − | + | * [[복소함수론]] | |
| + | * [[미분기하학]] | ||
| + | * 3차원 다양체 | ||
| − | + | ||
| − | + | ==관련된 항목들== | |
| + | * [[ 케일리 뫼비우스 변환]] | ||
| + | * [[17 Plane Crystallographic groups]] | ||
| + | * [[유한반사군과 콕세터군(finite reflection groups and Coxeter groups)]] | ||
| + | * [[모듈라 군, j-invariant and the singular moduli]] | ||
| + | * [[나비정리]] | ||
| + | * [[반전 사상(inversion)]] | ||
| − | + | ||
| − | + | ==매스매티카 파일 및 계산 리소스== | |
| − | + | * https://docs.google.com/file/d/0B8XXo8Tve1cxU3RVaWt6OUJrZ3c/edit | |
| − | < | + | |
| + | ==리뷰, 에세이, 강의노트== | ||
| + | * [http://www.jstor.org/stable/3616383 Finite Groups, Wallpaper Patterns and Non-Euclidean Geometries] | ||
| + | ** A. F. Beardon, <cite>The Mathematical Gazette</cite>, Vol. 62, No. 422 (Dec., 1978), pp. 267-278 | ||
| − | |||
| − | + | ==관련논문== | |
| + | * Knibbeler, Vincent, Sara Lombardo, and Jan A. Sanders. “Isotypical Components of Rational Functions.” arXiv:1511.06327 [math-Ph], November 19, 2015. http://arxiv.org/abs/1511.06327. | ||
| − | + | ==관련도서== | |
| − | + | * [http://www.amazon.com/Geometry-Discrete-Groups-Graduate-Mathematics/dp/0387907882 The Geometry of Discrete Groups (Graduate Texts in Mathematics)] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * [http://www.amazon.com/Geometry-Discrete-Groups-Graduate-Mathematics/dp/0387907882 The Geometry of Discrete Groups (Graduate Texts in Mathematics)] | ||
** Alan F. Beardon | ** Alan F. Beardon | ||
| − | * [http://www.amazon.com/Complex-Functions-Algebraic-Geometric-Viewpoint/dp/052131366X/ref=sr_1_1?ie=UTF8&s=books&qid=1224376763&sr=1-1 Complex Functions: An Algebraic and Geometric Viewpoint] | + | * [http://www.amazon.com/Complex-Functions-Algebraic-Geometric-Viewpoint/dp/052131366X/ref=sr_1_1?ie=UTF8&s=books&qid=1224376763&sr=1-1 Complex Functions: An Algebraic and Geometric Viewpoint] |
| − | ** Gareth A. Jones and David Singerman | + | ** Gareth A. Jones and David Singerman |
| − | * | + | * [http://www.amazon.com/Indras-Pearls-Vision-Felix-Klein/dp/0521352533 Indra's Pearls: The Vision of Felix Klein] |
** Mumford, David; Series, Caroline; Wright, David | ** Mumford, David; Series, Caroline; Wright, David | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==사전형태의 자료== | |
| − | |||
| − | |||
* http://ko.wikipedia.org/wiki/ | * http://ko.wikipedia.org/wiki/ | ||
| + | * [http://en.wikipedia.org/wiki/M%C3%B6bius_transformation http://en.wikipedia.org/wiki/Möbius_transformation] | ||
* http://en.wikipedia.org/wiki/Projective_transformation | * http://en.wikipedia.org/wiki/Projective_transformation | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ==동영상== | |
| − | + | * [http://www.youtube.com/watch?v=JX3VmDgiFnY Moebius Transformations Revealed] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * [http://www.youtube.com/watch?v=JX3VmDgiFnY Moebius Transformations Revealed] | ||
** Youtube | ** Youtube | ||
** 동영상으로 보는 뫼비우스 변환의 아름다움. | ** 동영상으로 보는 뫼비우스 변환의 아름다움. | ||
** 다양한 뫼비우스 변환이 처음의 사각형을 어떻게 바꾸는지를 보여줌. | ** 다양한 뫼비우스 변환이 처음의 사각형을 어떻게 바꾸는지를 보여줌. | ||
** 뫼비우스 변환은 복소평면보다 리만구면에 정의된 변환으로 이해하는 것이 바람직한 이해. | ** 뫼비우스 변환은 복소평면보다 리만구면에 정의된 변환으로 이해하는 것이 바람직한 이해. | ||
| + | [[분류:복소함수론]] | ||
| + | |||
| + | ==메타데이터== | ||
| + | ===위키데이터=== | ||
| + | * ID : [https://www.wikidata.org/wiki/Q595742 Q595742] | ||
| + | ===Spacy 패턴 목록=== | ||
| + | * [{'LOWER': 'möbius'}, {'LEMMA': 'transformation'}] | ||
2021년 2월 17일 (수) 05:43 기준 최신판
개요
- 복소평면 (더 정확히는 리만구면) 상의 복소수를, 또다른 복소수로 보내는 함수
- \(a,b,c,d\in\Bbb{C} \mbox{ and } ad-bc \ne 0\)일 때, 뫼비우스 변환은 다음과 같이 주어짐
\[f(z) = \frac{az+b}{cz+d}\]
- 하나의 뫼비우스변환은 \(GL(2,\mathbb{C})\)의 원소로 표현되지만, 행렬들의 상수배정도는 모두 똑같은 역할을 하므로, 전체 뫼비우스변환군은 \(PGL(2,\mathbb{C})\)와 동형인 군이 됨.
- 겹선형(bilinear) 또는 linear fractional transformation 으로 불리기도 함.
- 해석함수로 각도와 방향을 보존함.
- 뫼비우스 변환은 복소평면보다 리만구면에 정의된 변환으로 이해하는 것이 바람직함.
- 리만구면 = 1차원 복소사영공간
- 원이나 직선들을 모두 원이나 직선으로 보냄. (직선을 반지름이 무한대인 원으로 생각한다면, 원을 원으로 보냄.)
- 교차비를 보존함.
- 기초적인 내용은 학부 수준의 복소함수론에서 배울 수 있음.
- 리만구에 작용하는 뫼비우스 변환들이 이루는 군의 분류 문제는 많은 수학의 분야와 밀접하게 관련.
반전 사상과 뫼비우스 변환
- 반전 사상(inversion)
- \(z \mapsto \frac{1}{\bar{z}}\) 는 복소평면 상에서 고전적인 반전 사상이 된다. 하지만 방향(orientation)을 보존하지 않으므로, 해석함수가 되지 않음.
- 뫼비우스 변환 \(z \mapsto \frac{1}{z}\) 는 고전적인 평면기하의 반전 사상과 복소평면 상에서 x축에 대한 대칭사상의 합성으로, 방향을 보존하게 되고, 해석함수가 됨.
한 점에서의 사영과 뫼비우스 변환
- 두 주어진 직선 A,B와 두 직선 밖의 주어진 점 \(P'\)가 있다.
- 직선 A 위의 점 \(P\)와 \(P'\)를 지나는 직선이 직선 B에서 만나는 점을 \(\pi(P)\) 라 하자.
- \(\pi :A \to B\) 를 이와 같이 정의할 수 있다.
- 직선이 아닌 원에 대해서도 마찬가지로 정의가 가능.
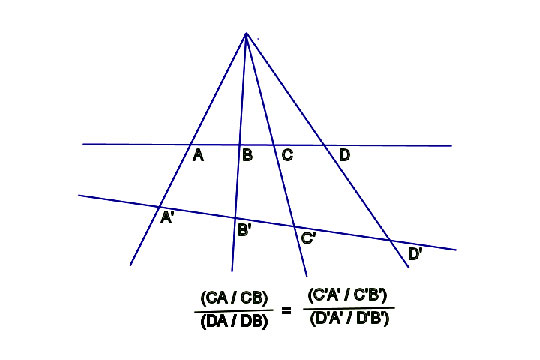
뫼비우스 변환과 원과 직선
- 직선의 방정식
- \(ax+by+c=0, a,b,c \in \mathbb{R}\)
- \(Bz+\bar{B}\bar{z}+c=0, z=x+iy, B=\frac{a}{2}-\frac{ib}{2}\)
- 두 표현은 같은 직선의 표현
- 원의 방정식
- \(|z-z_0|=\rho\)
- \(z\bar{z}+\bar{B}z+B\bar{z}+c=0, B=-z_0, c=|B|^2-\rho^2\)
- 두 표현은 같은 원의 표현
- 따라서 \(az\bar{z}+\bar{B}z+{B}\bar{z}+c=0, a,c\in \mathbb{R}\) 는 원과 직선의 방정식이 됨.
- 뫼비우스 변환은 이러한 형태의 식을 보존하므로, 원과 직선을 원과 직선으로 보냄.
교차비와 뫼비우스 변환
- 뫼비우스 변환이 네 점, \(z_1,z_2,z_3,z_4\) 를 \(w_1,w_2,w_3,w_4\)로 보내는 경우, 교차비는 보존됨.
\[\frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)} = \frac{(w_1-w_3)(w_2-w_4)}{(w_2-w_3)(w_1-w_4)}\]
- 교차비를 보존하는 복소함수가 네 점 \(z,z_2,z_3,z_4\)를 \(w,1,0,\infty\)로 보낼 경우, \((z,z_2;z_3,z_4) =(w,1;0,\infty)\) 로부터 다음의 뫼비우스변환을 유도할 수 있음
\[w = \frac{(z-z_3)(z_2-z_4)}{(z_2-z_3)(z-z_4)}\]
- 교차비(cross ratio) 항목 참조
세 점
- 사영기하학의 관점에서 \(\{0,1,\infty\}\)의 선택이 좋은 이유
- \(0\) 은 기준점의 역할
- \(1\) 은 단위길이를 결정
The first set of fixed points is {0, 1, ∞}. However, the cross-ratio can never take on these values if the points {zi} are all distinct. These values are limit values as one pair of coordinates approach each other:
\[(z,z_2;z,z_4) = (z_1,z;z_3,z) = 0\,\] \[(z,z;z_3,z_4) = (z_1,z_2;z,z) = 1\,\] \[(z,z_2;z_3,z) = (z_1,z;z,z_4) = \infty.\]
메모
- 사영기하학과 뫼비우스 변환
- Cross ratio
- central projection and cross ratio
- inversion and cross ratio
- Steiner's theorem
관련된 고교수학 또는 대학수학
관련된 항목들
- 케일리 뫼비우스 변환
- 17 Plane Crystallographic groups
- 유한반사군과 콕세터군(finite reflection groups and Coxeter groups)
- 모듈라 군, j-invariant and the singular moduli
- 나비정리
- 반전 사상(inversion)
매스매티카 파일 및 계산 리소스
리뷰, 에세이, 강의노트
- Finite Groups, Wallpaper Patterns and Non-Euclidean Geometries
- A. F. Beardon, The Mathematical Gazette, Vol. 62, No. 422 (Dec., 1978), pp. 267-278
관련논문
- Knibbeler, Vincent, Sara Lombardo, and Jan A. Sanders. “Isotypical Components of Rational Functions.” arXiv:1511.06327 [math-Ph], November 19, 2015. http://arxiv.org/abs/1511.06327.
관련도서
- The Geometry of Discrete Groups (Graduate Texts in Mathematics)
- Alan F. Beardon
- Complex Functions: An Algebraic and Geometric Viewpoint
- Gareth A. Jones and David Singerman
- Indra's Pearls: The Vision of Felix Klein
- Mumford, David; Series, Caroline; Wright, David
사전형태의 자료
- http://ko.wikipedia.org/wiki/
- http://en.wikipedia.org/wiki/Möbius_transformation
- http://en.wikipedia.org/wiki/Projective_transformation
동영상
- Moebius Transformations Revealed
- Youtube
- 동영상으로 보는 뫼비우스 변환의 아름다움.
- 다양한 뫼비우스 변환이 처음의 사각형을 어떻게 바꾸는지를 보여줌.
- 뫼비우스 변환은 복소평면보다 리만구면에 정의된 변환으로 이해하는 것이 바람직한 이해.
메타데이터
위키데이터
- ID : Q595742
Spacy 패턴 목록
- [{'LOWER': 'möbius'}, {'LEMMA': 'transformation'}]