"반전 사상(inversion)"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| (같은 사용자의 중간 판 5개는 보이지 않습니다) | |||
| 3번째 줄: | 3번째 줄: | ||
* 평면상에 직선이 주어져 있을 때, 평면위의 한 점을 그 직선에 대칭되는 점으로 보낼 수 있음. | * 평면상에 직선이 주어져 있을 때, 평면위의 한 점을 그 직선에 대칭되는 점으로 보낼 수 있음. | ||
* 그에 대응되는 개념으로, 평면상에 원이 하나 주어져 있을때, 점들을 그 원에 대칭인 점들로 보내는 사상을 '반전(inversion)이라 함. | * 그에 대응되는 개념으로, 평면상에 원이 하나 주어져 있을때, 점들을 그 원에 대칭인 점들로 보내는 사상을 '반전(inversion)이라 함. | ||
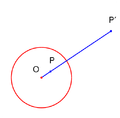
| − | * 두 점 P,P'가 주어진 | + | * 두 점 P,P'가 주어진 원에 대해 대칭이라는 조건은 다음과 같이 정의할 수 있음. |
** 두 점 P와 P'를 지나는 모든 직선과 원이 주어진 원과 수직으로 만남. | ** 두 점 P와 P'를 지나는 모든 직선과 원이 주어진 원과 수직으로 만남. | ||
| − | ** 동치조건으로, 원의 반지름이 r 인경우 다음과 같은 조건을 만족시킬 때 | + | ** 동치조건으로, 원의 반지름이 r 인경우 다음과 같은 조건을 만족시킬 때[[파일:1983652-120px-Inversion_illustration1.png]]:<math>OP\cdot OP'=r^2</math> |
* n차원 공간에서도 정의되며, [[등각 사상 (conformal mapping)]]이다 | * n차원 공간에서도 정의되며, [[등각 사상 (conformal mapping)]]이다 | ||
| − | + | ||
| − | + | ||
==리만구면상에서의 반전 사상== | ==리만구면상에서의 반전 사상== | ||
| − | * 평면상에서의 반전 | + | * 평면상에서의 반전 사상은 복소 리만 구면 상의 회전변환을 통하여 잘 이해할 수 있음. |
| − | + | ||
| − | + | ||
==반전 사상과 쌍곡기하학== | ==반전 사상과 쌍곡기하학== | ||
| − | |||
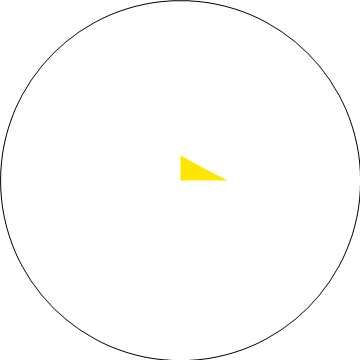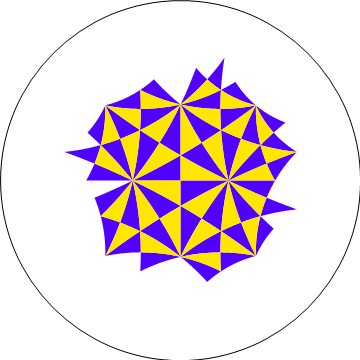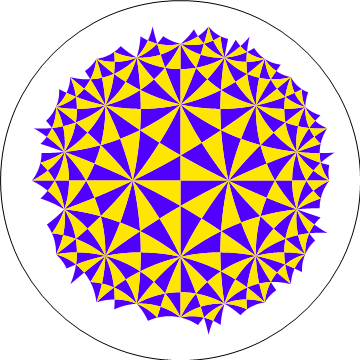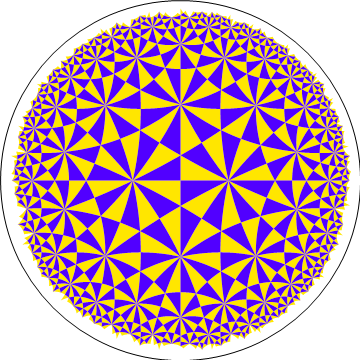
* 반전을 반복할 때 얻을 수 있는 종류의 그림 | * 반전을 반복할 때 얻을 수 있는 종류의 그림 | ||
| − | [[파일: | + | [[파일:237테셀레이션.gif]] |
| − | * 반전 | + | * [[반전 사상(inversion)]]은 [[푸앵카레 unit disk 모델]]에서, 모든 점들의 길이를 보존하는 등거리사상 |
* 따라서 위의 그림에 있는 삼각형들은 쌍곡기하학의 관점에서 보면, 모두 그 크기와 모양이 똑같음. | * 따라서 위의 그림에 있는 삼각형들은 쌍곡기하학의 관점에서 보면, 모두 그 크기와 모양이 똑같음. | ||
* [[2차원 쌍곡기하학의 테셀레이션]] 항목 참조 | * [[2차원 쌍곡기하학의 테셀레이션]] 항목 참조 | ||
| − | + | ||
==n차원 유클리드 공간에서의 반전 사상== | ==n차원 유클리드 공간에서의 반전 사상== | ||
| − | * 중심이 | + | * 중심이 <math>a\in \mathbb{R}^n</math>이고, 반지름이 <math>r>0</math>인 구면 <math>\{x\in \mathbb{R}^n|x-a|=r\}</math>에 대하여, <math>x</math>의 반전 <math>x'</math>은 다음과 같이 주어진다 |
| − | + | :<math> | |
x'=\frac{r^2(x-a)}{|x-a|^2}+a | x'=\frac{r^2(x-a)}{|x-a|^2}+a | ||
| − | + | </math> | |
| − | * [[등각 사상 (conformal mapping)]]에서의 정의를 따르면, conformal factor | + | * [[등각 사상 (conformal mapping)]]에서의 정의를 따르면, conformal factor <math>\Omega</math>는 다음과 같이 주어진다 |
| − | + | :<math> | |
\Omega=\frac{r^2}{(x-a)\cdot (x-a)} | \Omega=\frac{r^2}{(x-a)\cdot (x-a)} | ||
| − | + | </math> | |
===2차원에서의 예=== | ===2차원에서의 예=== | ||
| − | * 중심이 | + | * 중심이 <math>(0,0)</math>이고, 반지름이 <math>1</math>인 원에 대하여, 반전은 다음과 같은 변환이 된다 |
| − | + | :<math> | |
(x,y)\mapsto (\frac{x}{x^2+y^2},\frac{y}{x^2+y^2}) | (x,y)\mapsto (\frac{x}{x^2+y^2},\frac{y}{x^2+y^2}) | ||
| − | + | </math> | |
| − | * conformal factor는 | + | * conformal factor는 :<math>\Omega=\frac{1}{\left(x^2+y^2\right)}</math>가 된다 |
| 51번째 줄: | 50번째 줄: | ||
[[파일:반전 사상(inversion)1.png]] | [[파일:반전 사상(inversion)1.png]] | ||
| − | + | ||
==관련된 대학 수학== | ==관련된 대학 수학== | ||
| 59번째 줄: | 58번째 줄: | ||
** 반전은 비유클리드기하학의 쌍곡기하학에서 등거리사상. | ** 반전은 비유클리드기하학의 쌍곡기하학에서 등거리사상. | ||
| − | + | ||
==관련된 항목들== | ==관련된 항목들== | ||
* [[반사 변환]] | * [[반사 변환]] | ||
| − | + | ||
==계산 리소스== | ==계산 리소스== | ||
* https://docs.google.com/file/d/0B8XXo8Tve1cxR1FBUkt1eTJoMkk/edit | * https://docs.google.com/file/d/0B8XXo8Tve1cxR1FBUkt1eTJoMkk/edit | ||
| − | + | ||
| − | + | ||
==관련논문== | ==관련논문== | ||
| − | * [http://www.jstor.org/stable/3026702 Circles and Spheres] | + | * [http://www.jstor.org/stable/3026702 Circles and Spheres] |
| − | ** G. D. Chakerian, | + | ** G. D. Chakerian, <cite>The Two-Year College Mathematics Journal</cite>, Vol. 11, No. 1 (Jan., 1980), pp. 26-4 |
| − | + | ||
==블로그== | ==블로그== | ||
| − | * [http://bomber0.byus.net/index.php/2008/10/22/836 비유클리드 기하학 입문(4) : 콕세터가 설명하는 반전(inversion)] | + | * [http://bomber0.byus.net/index.php/2008/10/22/836 비유클리드 기하학 입문(4) : 콕세터가 설명하는 반전(inversion)] (피타고라스의 창) |
| − | * [http://bomber0.byus.net/index.php/2008/10/22/839 비유클리드 기하학 입문(5) : 반전에 반전 … 반전만 구백번…] | + | * [http://bomber0.byus.net/index.php/2008/10/22/839 비유클리드 기하학 입문(5) : 반전에 반전 … 반전만 구백번…] (피타고라스의 창) |
[[분류:중학수학]] | [[분류:중학수학]] | ||
[[분류:기하학적 변환]] | [[분류:기하학적 변환]] | ||
| + | [[분류:테셀레이션]] | ||
2020년 12월 28일 (월) 03:24 기준 최신판
개요
- 평면상에 직선이 주어져 있을 때, 평면위의 한 점을 그 직선에 대칭되는 점으로 보낼 수 있음.
- 그에 대응되는 개념으로, 평면상에 원이 하나 주어져 있을때, 점들을 그 원에 대칭인 점들로 보내는 사상을 '반전(inversion)이라 함.
- 두 점 P,P'가 주어진 원에 대해 대칭이라는 조건은 다음과 같이 정의할 수 있음.
- 두 점 P와 P'를 지나는 모든 직선과 원이 주어진 원과 수직으로 만남.
- 동치조건으로, 원의 반지름이 r 인경우 다음과 같은 조건을 만족시킬 때
\[OP\cdot OP'=r^2\]
- n차원 공간에서도 정의되며, 등각 사상 (conformal mapping)이다
리만구면상에서의 반전 사상
- 평면상에서의 반전 사상은 복소 리만 구면 상의 회전변환을 통하여 잘 이해할 수 있음.
반전 사상과 쌍곡기하학
- 반전을 반복할 때 얻을 수 있는 종류의 그림
- 반전 사상(inversion)은 푸앵카레 unit disk 모델에서, 모든 점들의 길이를 보존하는 등거리사상
- 따라서 위의 그림에 있는 삼각형들은 쌍곡기하학의 관점에서 보면, 모두 그 크기와 모양이 똑같음.
- 2차원 쌍곡기하학의 테셀레이션 항목 참조
n차원 유클리드 공간에서의 반전 사상
- 중심이 \(a\in \mathbb{R}^n\)이고, 반지름이 \(r>0\)인 구면 \(\{x\in \mathbb{R}^n|x-a|=r\}\)에 대하여, \(x\)의 반전 \(x'\)은 다음과 같이 주어진다
\[ x'=\frac{r^2(x-a)}{|x-a|^2}+a \]
- 등각 사상 (conformal mapping)에서의 정의를 따르면, conformal factor \(\Omega\)는 다음과 같이 주어진다
\[ \Omega=\frac{r^2}{(x-a)\cdot (x-a)} \]
2차원에서의 예
- 중심이 \((0,0)\)이고, 반지름이 \(1\)인 원에 대하여, 반전은 다음과 같은 변환이 된다
\[ (x,y)\mapsto (\frac{x}{x^2+y^2},\frac{y}{x^2+y^2}) \]
- conformal factor는 \[\Omega=\frac{1}{\left(x^2+y^2\right)}\]가 된다
3차원에서의 예
- 붉은색 점들과 푸른색 점들은 구면에 대하여 서로 반전의 위치에 놓여 있다
1.png)
관련된 대학 수학
관련된 항목들
계산 리소스
관련논문
- Circles and Spheres
- G. D. Chakerian, The Two-Year College Mathematics Journal, Vol. 11, No. 1 (Jan., 1980), pp. 26-4
블로그
- 비유클리드 기하학 입문(4) : 콕세터가 설명하는 반전(inversion) (피타고라스의 창)
- 비유클리드 기하학 입문(5) : 반전에 반전 … 반전만 구백번… (피타고라스의 창)