"삼각함수"의 두 판 사이의 차이
(피타고라스님이 이 페이지에 circularmotion.gif 파일을 등록하셨습니다.) |
Pythagoras0 (토론 | 기여) |
||
| (사용자 2명의 중간 판 41개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* 중학교에서 배운 삼각비를 실수 전체에서 정의된 함수로 확장하여 얻어지는 함수 | * 중학교에서 배운 삼각비를 실수 전체에서 정의된 함수로 확장하여 얻어지는 함수 | ||
| − | * 주기성을 가지며 삼각함수들 | + | * 주기성을 가지며 삼각함수들 사이에 많은 공식이 성립 |
| − | * 삼각비와 삼각함수의 차이에 | + | * 삼각비와 삼각함수의 차이에 대해서는 [[삼각비에서 삼각함수로]] 항목을 참조 |
* 삼각함수는 다양한 관점에서 이해가능하며, 각 관점에 따라 많은 방식으로 일반화된다 | * 삼각함수는 다양한 관점에서 이해가능하며, 각 관점에 따라 많은 방식으로 일반화된다 | ||
| − | * 삼각함수가 수학에서 차지하는 중요성을 알기 | + | * 삼각함수가 수학에서 차지하는 중요성을 알기 위해서는 [[삼각함수의 일반화]] 항목을 참조 |
| − | + | ||
| − | + | ||
| − | + | ==배우기 전에 알고 있어야 하는 것들== | |
* [[피타고라스의 정리]] | * [[피타고라스의 정리]] | ||
* [[원의 방정식]] | * [[원의 방정식]] | ||
| − | + | ||
| − | + | ||
| − | + | ==사인과 코사인== | |
| − | * 단위원의 방정식 | + | * 단위원의 방정식:<math>x^2+y^2=1</math> |
| − | * [[원 위에서 각도함수 정의하기]] | + | * [[원 위에서 각도함수 정의하기]] 작업을 통해 단위원의 각 점에 해당하는 각도 <math>\theta</math>를 정의할 수 있다 |
| − | * 코사인과 사인함수는 | + | * 코사인과 사인함수는 각각 각도 <math>\theta</math>에 해당하는 단위원의 점의 x-좌표와 y-좌표로 정의된다 |
| − | * 단위원의 좌표로 함수가 정의되므로, 다음 공식을 만족시킨다 | + | * 단위원의 좌표로 함수가 정의되므로, 다음 공식을 만족시킨다:<math>\cos^2\theta + \sin^2\theta = 1</math> |
| − | + | ||
| − | + | ==탄젠트와 코탄젠트, 시컨트와 코시컨트== | |
* <math>1 + \tan^2\theta = \sec^2\theta</math> | * <math>1 + \tan^2\theta = \sec^2\theta</math> | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ==삼각함수의 여러가지 공식들== | |
| − | * 삼각함수에 공식이 많은 이유는 삼각함수가 단위원의 매개함수로 정의되며, | + | * 삼각함수에 공식이 많은 이유는 삼각함수가 단위원의 매개함수로 정의되며, 단위원은 군(group)의 구조를 가지는 다양체이기 때문 |
| − | ** 군의 개념에 | + | ** 군의 개념에 대해서는 [[군론(group theory)|군론]] 항목을 참조 |
| − | * 더 자세한 | + | * 더 자세한 사항은 [[삼각함수에는 왜 공식이 많은가?]] 항목을 참조 |
| − | + | ||
| − | + | ||
| − | + | ==덧셈공식== | |
| − | <math>\sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta | + | <math>\sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta</math> |
| − | <math>\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta | + | <math>\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta</math> |
<math>\tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}</math> | <math>\tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}</math> | ||
| − | + | ==배각공식== | |
| − | |||
| − | |||
| − | |||
| − | |||
* 2배각공식과 3배각 공식 | * 2배각공식과 3배각 공식 | ||
| − | <math>\sin 2\theta | + | <math>\sin 2\theta = 2 \sin \theta \cos \theta</math> |
| − | <math>\cos 2\theta | + | <math>\cos 2\theta = \cos^2 \theta - \sin^2 \theta = 2 \cos^2 \theta - 1</math> |
<math>\tan 2\theta = \frac{2 \tan \theta} {1 - \tan^2 \theta}</math> | <math>\tan 2\theta = \frac{2 \tan \theta} {1 - \tan^2 \theta}</math> | ||
| 89번째 줄: | 77번째 줄: | ||
* 더 일반적인 경우에 대해서는 [[삼각함수의 배각공식 표]] 항목과 [[체비셰프 다항식]] 참조 | * 더 일반적인 경우에 대해서는 [[삼각함수의 배각공식 표]] 항목과 [[체비셰프 다항식]] 참조 | ||
| − | + | ==반각공식== | |
| − | |||
| − | |||
| − | |||
| − | |||
<math>\sin^2 \frac{\theta}{2} =\frac{1 - \cos \theta}{2}</math> | <math>\sin^2 \frac{\theta}{2} =\frac{1 - \cos \theta}{2}</math> | ||
| 99번째 줄: | 83번째 줄: | ||
<math>\cos^2 \frac{\theta}{2} = \frac{1 + \cos\theta}{2}</math> | <math>\cos^2 \frac{\theta}{2} = \frac{1 + \cos\theta}{2}</math> | ||
| − | + | ||
| − | + | ||
| − | + | ==삼각함수의 값== | |
* [[삼각함수의 값]] | * [[삼각함수의 값]] | ||
| − | + | ||
| − | + | ||
| − | + | ==삼각함수의 급수 표현== | |
* 사인함수와 코사인함수의 급수표현은 미적분학 강의를 통해서도 잘 배우지만, 탄젠트는 거의 언급되지 않음. | * 사인함수와 코사인함수의 급수표현은 미적분학 강의를 통해서도 잘 배우지만, 탄젠트는 거의 언급되지 않음. | ||
* 그 이유는, 표현에 베르누이수가 필요하기 때문. | * 그 이유는, 표현에 베르누이수가 필요하기 때문. | ||
| − | + | ||
<math>\tan x = x + \frac{x^3}{3} + \frac{2 x^5}{15} + \frac{17 x^7}{315} + \cdots =\sum_{n=1}^\infty \frac{(-1)^{n-1} 2^{2n} (2^{2n}-1) B_{2n} x^{2n-1}}{(2n)!}</math> | <math>\tan x = x + \frac{x^3}{3} + \frac{2 x^5}{15} + \frac{17 x^7}{315} + \cdots =\sum_{n=1}^\infty \frac{(-1)^{n-1} 2^{2n} (2^{2n}-1) B_{2n} x^{2n-1}}{(2n)!}</math> | ||
| 124번째 줄: | 108번째 줄: | ||
* [[베르누이 수]] 참조 | * [[베르누이 수]] 참조 | ||
| − | + | ||
| − | |||
| − | |||
| − | + | ||
| − | + | ==쌍곡함수== | |
| − | + | * [[쌍곡함수]] :<math>\coth x = \frac{\cosh x}{\sinh x} = \frac {\frac {e^x + e^{-x}} {2}} {\frac {e^x - e^{-x}} {2}} = \frac {e^x + e^{-x}} {e^x - e^{-x}} = \frac{e^{2x} + 1} {e^{2x} - 1} = i \cot ix </math> | |
| − | + | ==삼각함수 표== | |
| − | |||
| − | |||
* http://www.kor.pe.kr/home/ref/sin_cos_tan.htm | * http://www.kor.pe.kr/home/ref/sin_cos_tan.htm | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ==역사== | |
* [http://jeff560.tripod.com/trigonometry.html Earliest Uses of Symbols for Trigonometric and Hyperbolic Functions] | * [http://jeff560.tripod.com/trigonometry.html Earliest Uses of Symbols for Trigonometric and Hyperbolic Functions] | ||
| − | * [[ | + | * [[수학사 연표]] |
| − | + | ||
| − | + | ||
| − | + | ==메모== | |
* http://bomber0.byus.net/index.php/2008/11/11/869 | * http://bomber0.byus.net/index.php/2008/11/11/869 | ||
* http://navercast.naver.com/science/math/3005 | * http://navercast.naver.com/science/math/3005 | ||
| − | |||
* [[렘니스케이트(lemniscate) 곡선의 길이와 타원적분|lemniscate 곡선의 길이와 타원적분]] | * [[렘니스케이트(lemniscate) 곡선의 길이와 타원적분|lemniscate 곡선의 길이와 타원적분]] | ||
| − | + | [[파일:1000Hz.wav]] | |
| − | + | [[파일:1970036-120deg.png]] | |
| − | |||
| − | |||
| − | |||
| − | + | ||
==== 하위페이지 ==== | ==== 하위페이지 ==== | ||
| − | * [[삼각함수]] | + | * [[삼각함수]] |
| − | ** [[라디안]] | + | ** [[구면삼각법]] |
| − | ** [[삼각비에서 삼각함수로]] | + | ** [[라디안]] |
| − | ** [[삼각치환]] | + | ** [[삼각비에서 삼각함수로]] |
| − | ** [[삼각함수에는 왜 공식이 많은가?]] | + | ** [[삼각치환]] |
| − | ** [[삼각함수와 쌍곡함수의 맥클로린 급수]] | + | *** [[1/(1+x^2)의 적분]] |
| − | ** [[삼각함수의 값]] | + | ** [[삼각함수 이야기 두번째 - 덧붙이는 말]] |
| − | ** [[삼각함수의 덧셈과 곱셈 공식]] | + | ** [[삼각함수에는 왜 공식이 많은가?]] |
| − | ** [[삼각함수의 배각공식 표]] | + | ** [[삼각함수와 쌍곡함수의 맥클로린 급수]] |
| − | ** [[삼각함수의 역사]] | + | ** [[삼각함수의 값]] |
| − | ** [[삼각함수의 일반화]] | + | *** [[삼각함수의 유리수 값]] |
| − | ** [[쌍곡함수]] | + | ** [[삼각함수의 덧셈과 곱셈 공식]] |
| − | ** [[역삼각함수]] | + | ** [[삼각함수의 무한곱 표현]] |
| − | ** [[원 위에서 각도함수 정의하기]] | + | ** [[삼각함수의 배각공식 표]] |
| − | ** [[원의 매개화와 삼각함수의 탄생]] | + | ** [[삼각함수의 역사]] |
| − | ** [[코탄젠트]] | + | ** [[삼각함수의 일반화]] |
| − | + | ** [[삼각함수의 적분]] | |
| − | + | ** [[쌍곡함수]] | |
| − | + | ** [[역삼각함수]] | |
| − | + | ** [[원 위에서 각도함수 정의하기]] | |
| + | ** [[원의 매개화와 삼각함수의 탄생]] | ||
| + | ** [[코탄젠트]] | ||
| − | + | ==관련된 개념 및 나중에 더 배우게 되는 것들== | |
| − | + | * [[미분과 적분]] | |
| − | |||
| − | * [[미분과 적분]] | ||
** 삼각함수의 미분과 적분 | ** 삼각함수의 미분과 적분 | ||
| − | * [[복소수]] | + | * [[복소수]] |
** 극형식표현 | ** 극형식표현 | ||
| − | + | ||
| − | + | ==관련있는 다른 과목== | |
| − | * 물리학 | + | * 물리학 |
** 단진동 | ** 단진동 | ||
** 파동 | ** 파동 | ||
| − | * 지구과학 | + | * 지구과학 |
** 지구의 크기 | ** 지구의 크기 | ||
| − | * 음악 | + | * 음악 |
** [[수학과 음악]] | ** [[수학과 음악]] | ||
| − | + | ||
| − | + | ||
| − | + | ==관련된 대학교 수학== | |
* [[일변수미적분학]] | * [[일변수미적분학]] | ||
* [[톨레미의 정리]] | * [[톨레미의 정리]] | ||
| − | + | ||
| − | + | ==관련된 항목들== | |
| − | |||
| − | |||
| + | * [[무리수와 초월수]] | ||
| + | * [[삼각함수에는 왜 공식이 많은가?|삼각함수에는 왜 공식이 많은가?]] | ||
* [[푸리에 해석]] | * [[푸리에 해석]] | ||
* [[유한군의 표현론]] | * [[유한군의 표현론]] | ||
| − | + | ||
| − | + | ||
| − | + | ==수학용어번역== | |
* http://www.google.com/dictionary?langpair=en|ko&q= | * http://www.google.com/dictionary?langpair=en|ko&q= | ||
| − | * [http://mathnet.kaist.ac.kr/mathnet/math_list.php?mode=list&ftype=&fstr= 대한수학회 수학 학술 용어집] | + | * [http://mathnet.kaist.ac.kr/mathnet/math_list.php?mode=list&ftype=&fstr= 대한수학회 수학 학술 용어집] |
** http://mathnet.kaist.ac.kr/mathnet/math_list.php?mode=list&ftype=eng_term&fstr= | ** http://mathnet.kaist.ac.kr/mathnet/math_list.php?mode=list&ftype=eng_term&fstr= | ||
| − | * [http://kms.or.kr/home/kor/board/bulletin_list_subject.asp?bulletinid=%7BD6048897-56F9-43D7-8BB6-50B362D1243A%7D&boardname=%BC%F6%C7%D0%BF%EB%BE%EE%C5%E4%B7%D0%B9%E6&globalmenu=7&localmenu=4 | + | * [http://kms.or.kr/home/kor/board/bulletin_list_subject.asp?bulletinid=%7BD6048897-56F9-43D7-8BB6-50B362D1243A%7D&boardname=%BC%F6%C7%D0%BF%EB%BE%EE%C5%E4%B7%D0%B9%E6&globalmenu=7&localmenu=4 대한수학회 수학용어한글화 게시판] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ==사전 형태의 자료== | |
* http://ko.wikipedia.org/wiki/ | * http://ko.wikipedia.org/wiki/ | ||
| 257번째 줄: | 233번째 줄: | ||
* http://www.wolframalpha.com/input/?i=cos+x | * http://www.wolframalpha.com/input/?i=cos+x | ||
| − | |||
| − | + | ||
| − | + | ||
| − | + | ==관련논문== | |
| − | * [http://dx.doi.org/10.1007/1-4020-2204-2_16 A Note on the History of Trigonometric Functions] | + | * [http://dx.doi.org/10.1007/1-4020-2204-2_16 A Note on the History of Trigonometric Functions] |
** Jean-Pierre Merlet, International Symposium on History of Machines and Mechanisms, 2004 | ** Jean-Pierre Merlet, International Symposium on History of Machines and Mechanisms, 2004 | ||
* http://www.jstor.org/action/doBasicSearch?Query= | * http://www.jstor.org/action/doBasicSearch?Query= | ||
| 271번째 줄: | 246번째 줄: | ||
* http://dx.doi.org/10.1007/1-4020-2204-2_16 | * http://dx.doi.org/10.1007/1-4020-2204-2_16 | ||
| − | + | ||
| − | |||
| − | + | ==블로그== | |
| − | + | * http://navercast.naver.com/science/math/3005 | |
| − | + | [[분류:삼각함수]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==메타데이터== | |
| − | + | ===위키데이터=== | |
| − | + | * ID : [https://www.wikidata.org/wiki/Q93344 Q93344] | |
| − | + | ===Spacy 패턴 목록=== | |
| − | + | * [{'LOWER': 'trigonometric'}, {'LEMMA': 'function'}] | |
| − | + | * [{'LOWER': 'circular'}, {'LEMMA': 'function'}] | |
| − | * | + | * [{'LOWER': 'trigonometric'}, {'LEMMA': 'function'}] |
| − | * | + | * [{'LOWER': 'trig'}, {'LEMMA': 'functions'}] |
| − | ** | + | * [{'LOWER': 'angle'}, {'LEMMA': 'function'}] |
| − | * [ | + | * [{'LOWER': 'goniometric'}, {'LEMMA': 'function'}] |
| − | * [ | ||
| − | * [ | ||
2021년 2월 17일 (수) 05:47 기준 최신판
개요
- 중학교에서 배운 삼각비를 실수 전체에서 정의된 함수로 확장하여 얻어지는 함수
- 주기성을 가지며 삼각함수들 사이에 많은 공식이 성립
- 삼각비와 삼각함수의 차이에 대해서는 삼각비에서 삼각함수로 항목을 참조
- 삼각함수는 다양한 관점에서 이해가능하며, 각 관점에 따라 많은 방식으로 일반화된다
- 삼각함수가 수학에서 차지하는 중요성을 알기 위해서는 삼각함수의 일반화 항목을 참조
배우기 전에 알고 있어야 하는 것들
사인과 코사인
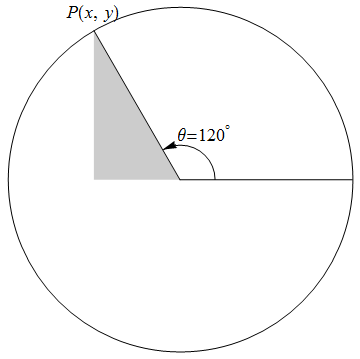
- 단위원의 방정식\[x^2+y^2=1\]
- 원 위에서 각도함수 정의하기 작업을 통해 단위원의 각 점에 해당하는 각도 \(\theta\)를 정의할 수 있다
- 코사인과 사인함수는 각각 각도 \(\theta\)에 해당하는 단위원의 점의 x-좌표와 y-좌표로 정의된다
- 단위원의 좌표로 함수가 정의되므로, 다음 공식을 만족시킨다\[\cos^2\theta + \sin^2\theta = 1\]
탄젠트와 코탄젠트, 시컨트와 코시컨트
- \(1 + \tan^2\theta = \sec^2\theta\)
삼각함수의 여러가지 공식들
- 삼각함수에 공식이 많은 이유는 삼각함수가 단위원의 매개함수로 정의되며, 단위원은 군(group)의 구조를 가지는 다양체이기 때문
- 군의 개념에 대해서는 군론 항목을 참조
- 더 자세한 사항은 삼각함수에는 왜 공식이 많은가? 항목을 참조
덧셈공식
\(\sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta\)
\(\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta\)
\(\tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}\)
배각공식
- 2배각공식과 3배각 공식
\(\sin 2\theta = 2 \sin \theta \cos \theta\)
\(\cos 2\theta = \cos^2 \theta - \sin^2 \theta = 2 \cos^2 \theta - 1\)
\(\tan 2\theta = \frac{2 \tan \theta} {1 - \tan^2 \theta}\)
\(\sin 3\theta = 3 \sin \theta - 4 \sin^3\theta\)
\(\cos 3\theta = 4 \cos^3\theta - 3 \cos \theta\)
- 더 일반적인 경우에 대해서는 삼각함수의 배각공식 표 항목과 체비셰프 다항식 참조
반각공식
\(\sin^2 \frac{\theta}{2} =\frac{1 - \cos \theta}{2}\)
\(\cos^2 \frac{\theta}{2} = \frac{1 + \cos\theta}{2}\)
삼각함수의 값
삼각함수의 급수 표현
- 사인함수와 코사인함수의 급수표현은 미적분학 강의를 통해서도 잘 배우지만, 탄젠트는 거의 언급되지 않음.
- 그 이유는, 표현에 베르누이수가 필요하기 때문.
\(\tan x = x + \frac{x^3}{3} + \frac{2 x^5}{15} + \frac{17 x^7}{315} + \cdots =\sum_{n=1}^\infty \frac{(-1)^{n-1} 2^{2n} (2^{2n}-1) B_{2n} x^{2n-1}}{(2n)!}\)
\(\cot x = \frac {1} {x} - \frac {x}{3} - \frac {x^3} {45} - \frac {2 x^5} {945} - \cdots = \sum_{n=0}^\infty \frac{(-1)^n 2^{2n} B_{2n} x^{2n-1}}{(2n)!}\)
- 베르누이 수 참조
쌍곡함수
- 쌍곡함수 \[\coth x = \frac{\cosh x}{\sinh x} = \frac {\frac {e^x + e^{-x}} {2}} {\frac {e^x - e^{-x}} {2}} = \frac {e^x + e^{-x}} {e^x - e^{-x}} = \frac{e^{2x} + 1} {e^{2x} - 1} = i \cot ix \]
삼각함수 표
역사
메모
- http://bomber0.byus.net/index.php/2008/11/11/869
- http://navercast.naver.com/science/math/3005
- lemniscate 곡선의 길이와 타원적분
하위페이지
관련된 개념 및 나중에 더 배우게 되는 것들
관련있는 다른 과목
- 물리학
- 단진동
- 파동
- 지구과학
- 지구의 크기
- 음악
관련된 대학교 수학
관련된 항목들
수학용어번역
사전 형태의 자료
- http://ko.wikipedia.org/wiki/
- http://en.wikipedia.org/wiki/Trigonometric_function
- http://en.wikipedia.org/wiki/List_of_trigonometric_identities
- http://en.wikipedia.org/wiki/Hyperbolic_function
- http://www.wolframalpha.com/input/?i=cos+x
관련논문
- A Note on the History of Trigonometric Functions
- Jean-Pierre Merlet, International Symposium on History of Machines and Mechanisms, 2004
- http://www.jstor.org/action/doBasicSearch?Query=
- http://www.ams.org/mathscinet
- http://dx.doi.org/10.1007/1-4020-2204-2_16
블로그
메타데이터
위키데이터
- ID : Q93344
Spacy 패턴 목록
- [{'LOWER': 'trigonometric'}, {'LEMMA': 'function'}]
- [{'LOWER': 'circular'}, {'LEMMA': 'function'}]
- [{'LOWER': 'trigonometric'}, {'LEMMA': 'function'}]
- [{'LOWER': 'trig'}, {'LEMMA': 'functions'}]
- [{'LOWER': 'angle'}, {'LEMMA': 'function'}]
- [{'LOWER': 'goniometric'}, {'LEMMA': 'function'}]