숫자 23과 다항식 x³-x+1
개요
- \(K=\mathbb{Q}(\sqrt{-23})\)
- 판별식이 \(\Delta=b^2-4ac=-23\)이 이차형식
\[x^2+xy+6y^2, 2x^2-xy+3y^2, 2x^2+xy+3y^2\]
- \(h(\Delta)=3\) 이 되는 첫번째 예
- 판별식이 작은 경우의 이차형식 목록 참조
- class field \(x^3-x+1\)의 해 \(\alpha\)에 대하여, \(H=K(\alpha)\)로 정의
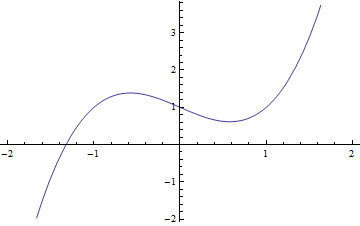
다항식 \(x^3-x+1\)
- 다항식의 판별식(discriminant)은 \(-4 a^3-27 b^2=-4(-1)^3-27=-23\)
- 다음과 같은 복소해를 가진다
\[ \{-1.32472,0.662359\, -0.56228 i,0.662359\, +0.56228 i\} \]
- 그래프
상호 법칙
- 정수론에서의 상호법칙 (reciprocity laws)
- 다항식 \(x^3-x+1 \pmod p\) 가 소수 \(p\) 에 따라 어떻게 분해되는지 혹은 몇 개의 근을 갖는지에 대한 질문
- 다음을 이용하여 답할 수 있다
\[ \begin{align} \eta(\tau)\eta(23\tau)&=q\prod_{n=1}^{\infty} (1-q^{n})(1-q^{23n})\\ {}&=q-q^2-q^3+q^6+q^8-q^{13}-q^{16}+q^{23}-q^{24}+q^{25}+q^{26}+q^{27}-q^{29}-q^{31}+q^{39}-q^{41}+\cdots \\ {}&=\sum_{n=1}^{\infty}a_n q^n \end{align} \] 여기서 \(\eta(\tau)\) 는 데데킨트 에타함수 \[\eta(\tau) = q^{1/24} \prod_{n=1}^{\infty} (1-q^{n}), \quad q=e^{2\pi i\tau}\]
- 소수 \(p\)에 대하여, \(c_p=-1+\#\{x\in \mathbb{F}_p|x^3-x+1=0\}\)라 두면, 다음이 성립한다
\[ a_p=c_p \]
- \(x^3-x+1 \pmod p\) 가 일차식으로 분해 \(\iff\) \(x^2+23y^2=p\) 의 정수해가 존재
테이블
\[ \begin{array}{c|c|c|c|c|c|c} p & p \bmod 23 & x^3-x+1 \pmod p & x^2+23y^2 & x^2+x y+6y^2 & 2x^2-x y+3y^2 & 2x^2+x y+3y^2 \\ \hline 2 & 2 & x^3+x+1 & 0 & 0 & 0 & 0 \\ 3 & 3 & x^3+2 x+1 & 0 & 0 & 0 & 0 \\ 5 & 5 & (x+2) \left(x^2+3 x+3\right) & 0 & 0 & 0 & 0 \\ 7 & 7 & (x+5) \left(x^2+2 x+3\right) & 0 & 0 & 0 & 0 \\ 11 & 11 & (x+6) \left(x^2+5 x+2\right) & 0 & 0 & 0 & 0 \\ 13 & 13 & x^3+12 x+1 & 0 & 0 & 0 & \{2,1\} \\ 17 & 17 & (x+5) \left(x^2+12 x+7\right) & 0 & 0 & 0 & 0 \\ 19 & 19 & (x+6) \left(x^2+13 x+16\right) & 0 & 0 & 0 & 0 \\ 23 & 0 & (x+3) (x+10)^2 & 0 & 0 & 0 & 0 \\ 29 & 6 & x^3+28 x+1 & 0 & 0 & \{2,3\} & 0 \\ 31 & 8 & x^3+30 x+1 & 0 & 0 & \{4,1\} & 0 \\ 37 & 14 & (x+13) \left(x^2+24 x+20\right) & 0 & 0 & 0 & 0 \\ 41 & 18 & x^3+40 x+1 & 0 & 0 & 0 & \{2,3\} \\ 43 & 20 & (x+10) \left(x^2+33 x+13\right) & 0 & 0 & 0 & 0 \\ 47 & 1 & x^3+46 x+1 & 0 & 0 & \{4,3\} & 0 \\ 53 & 7 & (x+37) \left(x^2+16 x+43\right) & 0 & 0 & 0 & 0 \\ 59 & 13 & (x+4) (x+13) (x+42) & \{6,1\} & \{5,2\} & 0 & 0 \\ 61 & 15 & (x+57) \left(x^2+4 x+15\right) & 0 & 0 & 0 & 0 \\ 67 & 21 & (x+7) \left(x^2+60 x+48\right) & 0 & 0 & 0 & 0 \\ 71 & 2 & x^3+70 x+1 & 0 & 0 & 0 & \{4,3\} \\ 73 & 4 & x^3+72 x+1 & 0 & 0 & \{2,5\} & 0 \\ 79 & 10 & (x+20) \left(x^2+59 x+4\right) & 0 & 0 & 0 & 0 \\ 83 & 14 & (x+66) \left(x^2+17 x+39\right) & 0 & 0 & 0 & 0 \\ 89 & 20 & (x+17) \left(x^2+72 x+21\right) & 0 & 0 & 0 & 0 \\ 97 & 5 & (x+51) \left(x^2+46 x+78\right) & 0 & 0 & 0 & 0 \\ 101 & 9 & (x+20) (x+89) (x+93) & \{3,2\} & \{1,4\} & 0 & 0 \\ 103 & 11 & (x+94) \left(x^2+9 x+80\right) & 0 & 0 & 0 & 0 \\ 107 & 15 & (x+34) \left(x^2+73 x+85\right) & 0 & 0 & 0 & 0 \\ 109 & 17 & (x+26) \left(x^2+83 x+21\right) & 0 & 0 & 0 & 0 \\ 113 & 21 & (x+54) \left(x^2+59 x+90\right) & 0 & 0 & 0 & 0 \\ 127 & 12 & x^3+126 x+1 & 0 & 0 & 0 & \{4,5\} \\ 131 & 16 & x^3+130 x+1 & 0 & 0 & \{8,3\} & 0 \\ 137 & 22 & (x+73) \left(x^2+64 x+122\right) & 0 & 0 & 0 & 0 \\ 139 & 1 & x^3+138 x+1 & 0 & 0 & 0 & \{8,1\} \\ 149 & 11 & (x+30) \left(x^2+119 x+5\right) & 0 & 0 & 0 & 0 \\ 151 & 13 & x^3+150 x+1 & 0 & 0 & \{4,7\} & 0 \\ 157 & 19 & (x+110) \left(x^2+47 x+10\right) & 0 & 0 & 0 & 0 \\ 163 & 2 & x^3+162 x+1 & 0 & 0 & \{8,5\} & 0 \\ 167 & 6 & (x+73) (x+127) (x+134) & \{12,1\} & \{11,2\} & 0 & 0 \\ 173 & 12 & (x+97) (x+110) (x+139) & \{9,2\} & \{7,4\} & 0 & 0 \\ 179 & 18 & x^3+178 x+1 & 0 & 0 & 0 & \{8,3\} \\ 181 & 20 & (x+30) \left(x^2+151 x+175\right) & 0 & 0 & 0 & 0 \\ 191 & 7 & (x+37) \left(x^2+154 x+31\right) & 0 & 0 & 0 & 0 \\ 193 & 9 & x^3+192 x+1 & 0 & 0 & \{10,1\} & 0 \\ 197 & 13 & x^3+196 x+1 & 0 & 0 & \{10,3\} & 0 \\ 199 & 15 & (x+54) \left(x^2+145 x+129\right) & 0 & 0 & 0 & 0 \\ 211 & 4 & (x+97) (x+120) (x+205) & \{2,3\} & 0 & 0 & 0 \\ 223 & 16 & (x+33) (x+63) (x+127) & \{4,3\} & \{1,6\} & 0 & 0 \\ 227 & 20 & (x+193) \left(x^2+34 x+20\right) & 0 & 0 & 0 & 0 \\ 229 & 22 & (x+43) \left(x^2+186 x+16\right) & 0 & 0 & 0 & 0 \end{array} \]
singular moduli
- 다음 세 다항식의
\[ x^2+x+6,2 x^2-x+3,2 x^2+x+3 \] 의 상반평면에서의 해를 구하여, 다음의 값을 생각하자 \[ j\left(\frac{1}{2} \left(-1+i \sqrt{23}\right)\right),j\left(\frac{1}{4} \left(1+i \sqrt{23}\right)\right),j\left(\frac{1}{4} \left(-1+i \sqrt{23}\right)\right)\] 여기서 \(j\)는 타원 모듈라 j-함수 (elliptic modular function, j-invariant)
- 이들은 대수적 정수이며, 다음 다항식의 해가 된다
\[ x^3+3491750 x^2-5151296875 x+12771880859375 \]
관련된 항목들
- 정수계수 이변수 이차형식(binary integral quadratic forms)
- 이차형식 x^2+27y^2
- 타원 모듈라 j-함수의 singular moduli
- 베버(Weber) 모듈라 함수
- 다항식 x³+x-1
계산 리소스
- https://docs.google.com/file/d/0B8XXo8Tve1cxTnFMSFZ2M2FtQkU/edit
- http://magma.maths.usyd.edu.au/users/volker/CompAlgSeminar/abstracts/kohel2.html
- https://oeis.org/A033217
- https://oeis.org/A106869
- https://oeis.org/A030199 G.f.: x * Product( (1 - x^k) * (1 - x^(23*k)), k=1..infinity).