"최단시간강하곡선 문제(Brachistochrone problem)"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
(→‎메타데이터: 새 문단)
 
(같은 사용자의 중간 판 하나는 보이지 않습니다)
95번째 줄: 95번째 줄:
 
* [http://curvebank.calstatela.edu/brach/brach.htm The Brachistochrone]
 
* [http://curvebank.calstatela.edu/brach/brach.htm The Brachistochrone]
 
[[분류:곡선]]
 
[[분류:곡선]]
 +
 +
== 노트 ==
 +
 +
===말뭉치===
 +
# More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp.<ref name="ref_9b3bb6c7">[https://en.wikipedia.org/wiki/Brachistochrone_curve Brachistochrone curve]</ref>
 +
# According to Newtonian scholar Tom Whiteside, in an attempt to outdo his brother, Jakob Bernoulli created a harder version of the brachistochrone problem.<ref name="ref_9b3bb6c7" />
 +
# Johann Bernoulli's direct method is historically important as it was the first proof that the brachistochrone is the cycloid.<ref name="ref_9b3bb6c7" />
 +
# In this blog post, we demonstrate how to use built-in mathematical expressions and the Optimization Module in COMSOL Multiphysics to solve for the brachistochrone curve.<ref name="ref_264bcfed">[https://www.comsol.com/blogs/how-to-solve-for-the-brachistochrone-curve-between-points/ How to Solve for the Brachistochrone Curve Between Points]</ref>
 +
# The brachistochrone curve is an idealized curve that provides the fastest descent possible.<ref name="ref_264bcfed" />
 +
# Next, we use an interpolation function to approximate the brachistochrone curve.<ref name="ref_264bcfed" />
 +
# The brachistochrone curve is a classic physics problem, that derives the fastest path between two points A and B which are at different elevations.<ref name="ref_aeddd8c4">[https://www.instructables.com/The-Brachistochrone-Curve/ The Brachistochrone Curve]</ref>
 +
# There is no better way to learn than through STEM, so follow on to make your very own working brachistochrone model.<ref name="ref_aeddd8c4" />
 +
# Before I end I must voice once more the admiration I feel for the unexpected identity of Huygens' tautochrone and my brachistochrone.<ref name="ref_4722e185">[https://mathshistory.st-andrews.ac.uk/HistTopics/Brachistochrone/ Brachistochrone problem]</ref>
 +
# This article presents the problem of quickest descent, or the Brachistochrone curve, that may be solved by the calculus of variations and the Euler-Lagrange equation.<ref name="ref_68ed8ad5">[https://www.tau.ac.il/~flaxer/edu/course/computerappl/exercise/Brachistochrone%20Curve.pdf Osaka keidai ronshu, vol. 61 no. 6 march 2011]</ref>
 +
# The rst step in the solution of the Euler-Lagrange equation for the brachistochrone problem: is to reduce it to a rst-order equation.<ref name="ref_ef0bb1d5">[http://www.math.utk.edu/~freire/teaching/m231f08/m231f08brachistochrone.pdf The brachistochrone problem.]</ref>
 +
# the red cycloid beats the other two It can also be asked what the brachistochrone curve among the curves joining two points and having a given shape would be.<ref name="ref_b32ffb35">[https://mathcurve.com/courbes2d.gb/brachistochrone/brachistochrone.shtml Brachistochrone]</ref>
 +
# For example, for two points at the same altitude and V-shaped curves, the brachistochrone curve is the one for which the angle of the V is a right angle, as is shown in the animation opposite.<ref name="ref_b32ffb35" />
 +
# The problem of the brachistochrone with given length is studied on this page.<ref name="ref_b32ffb35" />
 +
# One can also try to find the brachistochrone "with friction".<ref name="ref_b32ffb35" />
 +
# The brachistochrone problem was one of the earliest problems posed in the calculus of variations.<ref name="ref_f5cca441">[https://mathworld.wolfram.com/BrachistochroneProblem.html Brachistochrone Problem -- from Wolfram MathWorld]</ref>
 +
# Brachistochrone, the planar curve on which a body subjected only to the force of gravity will slide (without friction) between two points in the least possible time.<ref name="ref_5bcf547e">[https://www.britannica.com/science/brachistochrone Brachistochrone | physics]</ref>
 +
# The name brachistochrone comes from two Greek words, brachistos meaning shortest, and chronos meaning time.<ref name="ref_02e66dfd">[https://www.myphysicslab.com/roller/brachistochrone-en.html myPhysicsLab Brachistochrone]</ref>
 +
# The brachistochrone curve can be generated by tracking a point on the rim of a wheel as it rolls on the ground.<ref name="ref_02e66dfd" />
 +
# This mathematical challenge is known as the problem of the brachistochrone.<ref name="ref_e19ac3b2">[https://medium.com/cantors-paradise/the-famous-problem-of-the-brachistochrone-8b955d24bdf7 The Famous Problem of the Brachistochrone]</ref>
 +
# Figure 3: Newton’s handwritten solution to the brachistochrone problem (source).<ref name="ref_e19ac3b2" />
 +
# The classical problem in calculus of variation is the so called brachistochrone problem 1 posed (and solved) by Bernoulli in 1696.<ref name="ref_69295678">[https://wiki.math.ntnu.no/_media/tma4180/2015v/calcvar.pdf Basics of calculus of variations]</ref>
 +
# Abstract: This article presents the problem of quickest descent, or the Brachistochrone curve, that may be solved by the calculus of variations and the Euler-Lagrange equation.<ref name="ref_b10a7db6">[https://ijpam.eu/contents/2013-82-3/8/8.pdf International journal of pure and applied mathematics]</ref>
 +
# Historically and pedagogically, the prototype problem introducing the cal- culus of variations is the brachistochrone, from the Greek for shortest time.<ref name="ref_15b1f6a4">[http://www.hep.caltech.edu/~fcp/math/variationalCalculus/variationalCalculus.pdf Physics 129a]</ref>
 +
===소스===
 +
<references />
 +
 +
== 메타데이터 ==
 +
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q529985 Q529985]
 +
===Spacy 패턴 목록===
 +
* [{'LOWER': 'brachistochrone'}, {'LEMMA': 'curve'}]
 +
* [{'LEMMA': 'brachistochrone'}]

2021년 2월 23일 (화) 19:09 기준 최신판

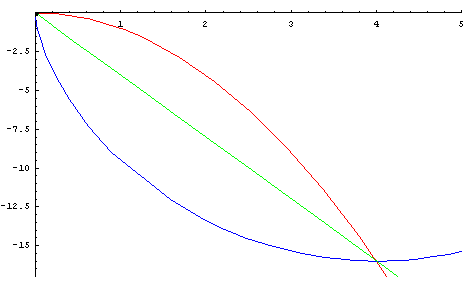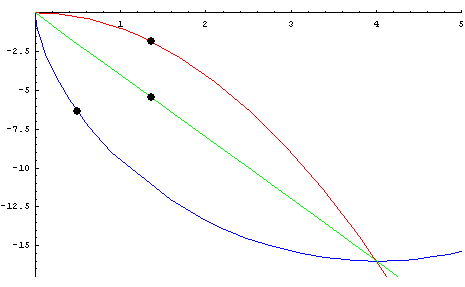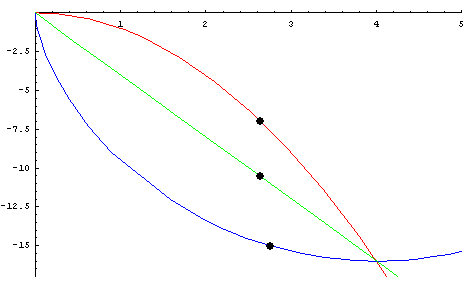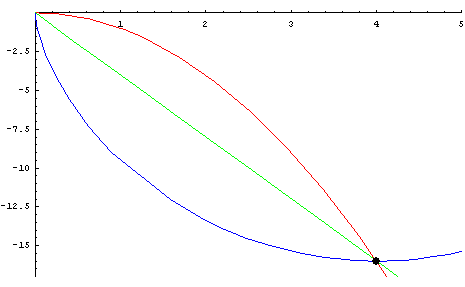
개요

  • 중력을 받고 있는 물체가 정지상태에서 출발하여 가장 짧은 시간내에 하강하기 위해서 따라야 하는 곡선
  • 1697년에 베르누이에 의하여 답이 출판

4402517-ParabNickF.gif


Classical Mechanics

곡선의 시작점을 \((x_0,y_0)=(0,0)\), 끝점을 \((x_1,y_1)\)라 두자.

곡선을 따라 내려올때 걸리는 시간은 다음과 같이 구할 수 있다.

\(t=\int \frac{1}{v} \, ds\)(v는 속력, ds 는 길이요소, t는 시간)

에너지 보존 법칙 \(mgy=\frac{1}{2}mv^2\) 에서\(v=\sqrt{2gy}\).

이제 곡선의 x좌표를 y의 함수로 생각하자. 곡선을 따라 내려올 때 걸리는 시간은 \[T=\int \frac{1}{v} \, ds=\frac{1}{\sqrt{2g}}\int_{0}^{y} \frac{\sqrt{1+x'(y)^2}}{\sqrt{y}} \, dy\]

문제의 정의에 따라 이 적분값을 최소가 되게 하는 곡선을 찾아야 한다.

\(F(y,x,x')=\frac{\sqrt{1+(x')^2}}{\sqrt{y}}\) 에 대하여 오일러-라그랑지 방정식 을 적용하면, \[0 =\frac{\partial F}{\partial x} - \frac{d}{dy} \frac{\partial F}{\partial x'}=-\frac{d}{dy}(\frac{x'(y)}{\sqrt{y(1+x'(y)^2)}})\]

적당한 상수 a에 대하여 \(\frac{x'(y)}{\sqrt{y(1+x'(y)^2)}}=\frac{1}{\sqrt{2a}}\)라 두자.

이를 풀면 다음의 미분방정식을 얻는다. \[\frac{dx}{dy}=\sqrt{\frac{y}{2a-y}}\]

(미분방정식의 여러 해에 대한 논의는 http://whistleralley.com/brachistochrone/brachistochrone.htm)

\(x=\int_{0}^{y}\sqrt{\frac{y}{2a-y}}dy\), \(y=2a\sin^2\frac{\theta}{2}=a(1-\cos\theta)\)로 치환하면, \(x=a(\theta-\sin\theta)\)를 얻는다.

여기서 상수 a는 주어진 점 \((x_1,y_1)\)를 지날 수 있는 값으로 결정된다.

따라서 사이클로이드를 얻었다.■



재미있는 사실


수학용어번역

  • Brachistochrone curve
    • brachistos - the shortest, chronos - time
    • 최단시간강하 곡선, 최속강하선, 최단강하선


관련된 항목들


매스매티카 파일 및 계산 리소스


사전 형태의 자료



관련논문



관련도서


링크

노트

말뭉치

  1. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp.[1]
  2. According to Newtonian scholar Tom Whiteside, in an attempt to outdo his brother, Jakob Bernoulli created a harder version of the brachistochrone problem.[1]
  3. Johann Bernoulli's direct method is historically important as it was the first proof that the brachistochrone is the cycloid.[1]
  4. In this blog post, we demonstrate how to use built-in mathematical expressions and the Optimization Module in COMSOL Multiphysics to solve for the brachistochrone curve.[2]
  5. The brachistochrone curve is an idealized curve that provides the fastest descent possible.[2]
  6. Next, we use an interpolation function to approximate the brachistochrone curve.[2]
  7. The brachistochrone curve is a classic physics problem, that derives the fastest path between two points A and B which are at different elevations.[3]
  8. There is no better way to learn than through STEM, so follow on to make your very own working brachistochrone model.[3]
  9. Before I end I must voice once more the admiration I feel for the unexpected identity of Huygens' tautochrone and my brachistochrone.[4]
  10. This article presents the problem of quickest descent, or the Brachistochrone curve, that may be solved by the calculus of variations and the Euler-Lagrange equation.[5]
  11. The rst step in the solution of the Euler-Lagrange equation for the brachistochrone problem: is to reduce it to a rst-order equation.[6]
  12. the red cycloid beats the other two It can also be asked what the brachistochrone curve among the curves joining two points and having a given shape would be.[7]
  13. For example, for two points at the same altitude and V-shaped curves, the brachistochrone curve is the one for which the angle of the V is a right angle, as is shown in the animation opposite.[7]
  14. The problem of the brachistochrone with given length is studied on this page.[7]
  15. One can also try to find the brachistochrone "with friction".[7]
  16. The brachistochrone problem was one of the earliest problems posed in the calculus of variations.[8]
  17. Brachistochrone, the planar curve on which a body subjected only to the force of gravity will slide (without friction) between two points in the least possible time.[9]
  18. The name brachistochrone comes from two Greek words, brachistos meaning shortest, and chronos meaning time.[10]
  19. The brachistochrone curve can be generated by tracking a point on the rim of a wheel as it rolls on the ground.[10]
  20. This mathematical challenge is known as the problem of the brachistochrone.[11]
  21. Figure 3: Newton’s handwritten solution to the brachistochrone problem (source).[11]
  22. The classical problem in calculus of variation is the so called brachistochrone problem 1 posed (and solved) by Bernoulli in 1696.[12]
  23. Abstract: This article presents the problem of quickest descent, or the Brachistochrone curve, that may be solved by the calculus of variations and the Euler-Lagrange equation.[13]
  24. Historically and pedagogically, the prototype problem introducing the cal- culus of variations is the brachistochrone, from the Greek for shortest time.[14]

소스

  1. ↑ 1.0 1.1 1.2 Brachistochrone curve
  2. ↑ 2.0 2.1 2.2 How to Solve for the Brachistochrone Curve Between Points
  3. ↑ 3.0 3.1 The Brachistochrone Curve
  4. ↑ Brachistochrone problem
  5. ↑ Osaka keidai ronshu, vol. 61 no. 6 march 2011
  6. ↑ The brachistochrone problem.
  7. ↑ 7.0 7.1 7.2 7.3 Brachistochrone
  8. ↑ Brachistochrone Problem -- from Wolfram MathWorld
  9. ↑ Brachistochrone | physics
  10. ↑ 10.0 10.1 myPhysicsLab Brachistochrone
  11. ↑ 11.0 11.1 The Famous Problem of the Brachistochrone
  12. ↑ Basics of calculus of variations
  13. ↑ International journal of pure and applied mathematics
  14. ↑ Physics 129a

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'brachistochrone'}, {'LEMMA': 'curve'}]
  • [{'LEMMA': 'brachistochrone'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=최단시간강하곡선_문제(Brachistochrone_problem)&oldid=52676"