"카탈란 수 (Catalan numbers)"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
(피타고라스님이 이 페이지의 이름을 카탈란 수로 바꾸었습니다.)
 
(사용자 2명의 중간 판 36개는 보이지 않습니다)
1번째 줄: 1번째 줄:
 +
==개요==
  
 +
* 조합수학에서 빈번하게 등장하는 수열의 하나
 +
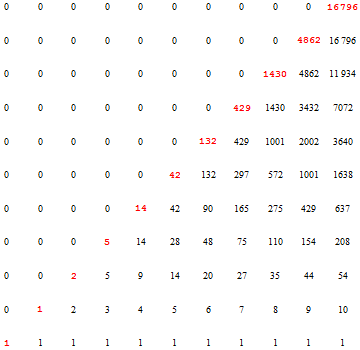
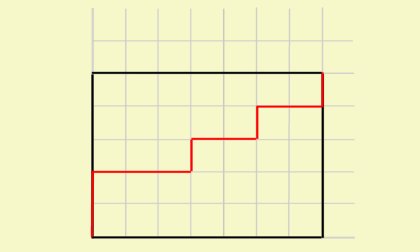
* (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 <math>y=x</math>를 넘지 않는 경우의 수
 +
* <math>n\geq 0 </math>에 대하여 다음과 같이 주어짐:<math>c_n = \frac{1}{n+1}{2n\choose n} = \frac{(2n)!}{(n+1)!\,n!}</math>
 +
*  1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012,…
 +
 +
[[파일:카탈란 수열(Catalan numbers)1.png]]
 +
 +
 +
 +
 +
==점화식==
 +
* 다음의 점화식이 성립한다
 +
<math>c_{n+1}=c_0c_n+c_1c_{n-1}+\cdots+c_nc_0 \label{rec}</math>
 +
* [[홀로노믹 수열]]
 +
:<math>
 +
(n+2)c_{n+1}+(-4 n-2)c_{n}=0
 +
</math>
 +
 +
 +
 +
 +
==생성함수==
 +
* 기본적인 내용에 대해서는  [[생성함수]] 항목을 참조
 +
* 카탈란 수열의 생성함수는 다음과 같이 주어짐
 +
:<math>G(x)= c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots=\frac{1-\sqrt{1-4x}}{2x}</math>
 +
 +
===증명===
 +
생성함수를 다음과 같이 두자
 +
:<math>G(x)= c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots</math>
 +
다음을 얻을 수 있다
 +
:<math>x G(x)^2= (c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots)^2=c_0^2x+(c_0c_1+c_1c_0)x^2+(c_0c_2+c_1c_1+c_2c_0)x^3+\cdots=G(x)-1</math>
 +
여기에 \ref{rec} 을 이용하면,
 +
:<math>x G(x)^2-G(x)+1=0</math>
 +
따라서
 +
:<math>G(x)= \frac{1-\sqrt{1-4x}}{2x}</math>■
 +
 +
 +
 +
 +
 +
==점근 급수==
 +
* 멱급수 <math>(1-x)^{-1/2}=\sum_{n=0}^{\infty} a_n x^n</math>의 계수는 다음과 같은 점근 급수를 갖는다
 +
:<math>
 +
a_n \sim \frac{1}{\sqrt{\pi n}}\left(1-\frac{1}{8 n}+\frac{1}{128 n^2}+\frac{5}{1024 n^3}+O(\frac{1}{n^4})\right)
 +
</math>
 +
* 카탈란 상수는 다음을 만족한다
 +
:<math>
 +
c_n=\frac{4^n}{n+1}a_n \sim \frac{4^n}{(n+1)\sqrt{\pi n}}\left(1-\frac{1}{8 n}+\frac{1}{128 n^2}+\frac{5}{1024 n^3}+O(\frac{1}{n^4})\right)
 +
</math>
 +
* [[스털링 공식]] 을 이용하여 다음을 증명할 수 있다
 +
:<math>c_{n}\sim \frac{4^{n}}{\sqrt{\pi n}(n+1)}(1-\frac{1}{8n})</math>
 +
* [[점근 급수(asymptotic series)]]
 +
 +
 +
 +
==격자경로와 카탈란 수==
 +
===증명의 아이디어===
 +
*  (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로의 수
 +
:<math>{2n \choose n}</math>
 +
*  (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 <math>y=x</math>를 넘지 않는 경우의 수 (카탈란 수)
 +
:<math>\frac{1}{n+1}{2n \choose n}</math>
 +
* (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수를 구한 다음, 그 중에서 y=x를 넘어서 가는 방법의 수를 빼면 된다. 이 방법의 수가 얼마가 되겠느냐를 구하는 과정에서 일대일대응이 등장한다.
 +
 +
 +
 +
===일단계===
 +
(0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수를 구해 보자. 이것은 매우 간단한 문제인데, 일대일대응을 통하여 문제를 풀어보자.  각 경로에서 x축으로 움직이는 것을 X로 표시하고 y축으로 움직이는 것을 Y로 표시하면, 각 경로는 X와Y를 n개 씩 쓴 문자열로 표현된다. 이것이 일대일 대응이다. 각각의 경로는 서로 다른 문자열로 표현될테고, 문자열은 또한 어떤 경로를 표현할테니까 말이다. 따라서 죽 늘어놓은 2n개 중에서 n개를 골라 X라고 써 놓으면 나머지 위치는 Y가 될 것이고 결정될 것이고, 그런 방법의 수는 <math>{2n \choose n}</math>이다. 즉, (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수는 <math>{2n \choose n}</math>이다.
 +
 +
 +
 +
===이단계===
 +
이제 직선 <math>y=x</math>를 넘어서서 가는 경로의 수를 구하자. 경로는 반드시 <math>y=x+1</math>과 만나게 될 것이다.
 +
 +
[[파일:카탈란 수열(Catalan numbers)meeting.jpg]]
 +
 +
이 때, 이 경로의 <math>(0,0)</math>에서부터 <math>y=x+1</math>과 처음으로 만나는 점까지를 잘라서, <math>y=x</math>에 대칭시키자.
 +
 +
[[파일:카탈란 수열(Catalan numbers)Symmetrization.jpg]]
 +
 +
그리고 나머지 경로를 평행이동시켜 대칭이동된 경로에 갖다붙이자.
 +
 +
[[파일:카탈란 수열(Catalan numbers)translation.jpg]]
 +
 +
그 결과는 <math>(0,0)</math>에서 출발하여 <math>(n+1,n-1)</math>에 도착하는 경로일 것이다.
 +
 +
[[파일:카탈란 수열(Catalan numbers)result.jpg]]
 +
 +
위에서 한 작업은 서로 다른 두 경로의 집합 사이에 어떤 대응을 만들어 낸 것이다. 이 대응은 일대일 대응이다. 일대일대응임을 보이기 위해서는 두 가지를 생각해야 한다. 첫번째는, 서로 다른 것으로 대응되었는지를 살피고, 두번째는 공역의 모든 원소가 대응되었는지를 살피는 것이다.
 +
 +
<math>y=x</math>를 넘어서서 가는 경로는 <math>(0,0)</math>에서 <math>(n+1,n-1)</math>까지 가는 경로와 일대일 대응되므로 그 개수는 <math>{2n \choose n+1}</math>이다.
 +
 +
따라서 처음에 제기했던 문제의 답은 다음과 같다
 +
:<math>{2n \choose n}-{2n \choose n+1}=\frac{1}{n+1}{2n \choose n}</math> ■
 +
 +
 +
 +
 +
 +
 +
 +
==적분표현==
 +
 +
* <math>c_n=\int_{0}^{1} 2^{2n+1}{\cos^{2n} \pi x}\, {\sin^2 \pi x}\,dx</math>
 +
 +
 +
 +
==역사==
 +
 +
* [[수학사 연표]]
 +
 +
 +
 +
 +
 +
==메모==
 +
* [http://bomber0.byus.net/index.php/2008/05/10/643 일대일대응 그리고 카탈란의 수(Catalan Numbers)]
 +
 +
 +
 +
==관련된 항목들==
 +
* [[정다각형의 삼각화]]
 +
* [[Dyck 경로]]
 +
* [[Associahedron]]
 +
* [[모츠킨 수 (Motzkin number)]]
 +
* [[격자 경로]]
 +
 +
 +
 +
==매스매티카 파일 및 계산 리소스==
 +
* [http://www.research.att.com/%7Enjas/sequences/index.html The On-Line Encyclopedia of Integer Sequences]
 +
** https://oeis.org/A000108
 +
 +
 +
 +
==사전 형태의 자료==
 +
 +
* http://ko.wikipedia.org/wiki/
 +
* http://en.wikipedia.org/wiki/Catalan_number
 +
 +
 +
 +
==리뷰, 에세이, 강의노트==
 +
* Pak, Igor. “History of Catalan Numbers.” arXiv:1408.5711 [math], August 25, 2014. http://arxiv.org/abs/1408.5711.
 +
 +
 +
 +
==관련도서==
 +
 +
* Thomas Koshy [http://www.amazon.com/exec/obidos/ASIN/019533454X/ref=nosim/addallbooksearch Catalan Numbers with Applications], Oxford University Press, USA, 2008
 +
 +
[[분류:조합수학]]
 +
[[분류:수열]]
 +
 +
==메타데이터==
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q270513 Q270513]
 +
===Spacy 패턴 목록===
 +
* [{'LOWER': 'catalan'}, {'LEMMA': 'number'}]

2021년 2월 17일 (수) 06:01 기준 최신판

개요

  • 조합수학에서 빈번하게 등장하는 수열의 하나
  • (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 \(y=x\)를 넘지 않는 경우의 수
  • \(n\geq 0 \)에 대하여 다음과 같이 주어짐\[c_n = \frac{1}{n+1}{2n\choose n} = \frac{(2n)!}{(n+1)!\,n!}\]
  • 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012,…

카탈란 수열(Catalan numbers)1.png



점화식

  • 다음의 점화식이 성립한다

\(c_{n+1}=c_0c_n+c_1c_{n-1}+\cdots+c_nc_0 \label{rec}\)

\[ (n+2)c_{n+1}+(-4 n-2)c_{n}=0 \]



생성함수

  • 기본적인 내용에 대해서는 생성함수 항목을 참조
  • 카탈란 수열의 생성함수는 다음과 같이 주어짐

\[G(x)= c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots=\frac{1-\sqrt{1-4x}}{2x}\]

증명

생성함수를 다음과 같이 두자 \[G(x)= c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots\] 다음을 얻을 수 있다 \[x G(x)^2= (c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots)^2=c_0^2x+(c_0c_1+c_1c_0)x^2+(c_0c_2+c_1c_1+c_2c_0)x^3+\cdots=G(x)-1\] 여기에 \ref{rec} 을 이용하면, \[x G(x)^2-G(x)+1=0\] 따라서 \[G(x)= \frac{1-\sqrt{1-4x}}{2x}\]■



점근 급수

  • 멱급수 \((1-x)^{-1/2}=\sum_{n=0}^{\infty} a_n x^n\)의 계수는 다음과 같은 점근 급수를 갖는다

\[ a_n \sim \frac{1}{\sqrt{\pi n}}\left(1-\frac{1}{8 n}+\frac{1}{128 n^2}+\frac{5}{1024 n^3}+O(\frac{1}{n^4})\right) \]

  • 카탈란 상수는 다음을 만족한다

\[ c_n=\frac{4^n}{n+1}a_n \sim \frac{4^n}{(n+1)\sqrt{\pi n}}\left(1-\frac{1}{8 n}+\frac{1}{128 n^2}+\frac{5}{1024 n^3}+O(\frac{1}{n^4})\right) \]

\[c_{n}\sim \frac{4^{n}}{\sqrt{\pi n}(n+1)}(1-\frac{1}{8n})\]


격자경로와 카탈란 수

증명의 아이디어

  • (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로의 수

\[{2n \choose n}\]

  • (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 \(y=x\)를 넘지 않는 경우의 수 (카탈란 수)

\[\frac{1}{n+1}{2n \choose n}\]

  • (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수를 구한 다음, 그 중에서 y=x를 넘어서 가는 방법의 수를 빼면 된다. 이 방법의 수가 얼마가 되겠느냐를 구하는 과정에서 일대일대응이 등장한다.


일단계

(0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수를 구해 보자. 이것은 매우 간단한 문제인데, 일대일대응을 통하여 문제를 풀어보자. 각 경로에서 x축으로 움직이는 것을 X로 표시하고 y축으로 움직이는 것을 Y로 표시하면, 각 경로는 X와Y를 n개 씩 쓴 문자열로 표현된다. 이것이 일대일 대응이다. 각각의 경로는 서로 다른 문자열로 표현될테고, 문자열은 또한 어떤 경로를 표현할테니까 말이다. 따라서 죽 늘어놓은 2n개 중에서 n개를 골라 X라고 써 놓으면 나머지 위치는 Y가 될 것이고 결정될 것이고, 그런 방법의 수는 \({2n \choose n}\)이다. 즉, (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수는 \({2n \choose n}\)이다.


이단계

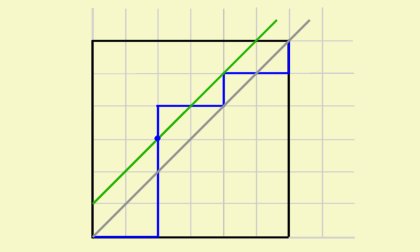
이제 직선 \(y=x\)를 넘어서서 가는 경로의 수를 구하자. 경로는 반드시 \(y=x+1\)과 만나게 될 것이다.

카탈란 수열(Catalan numbers)meeting.jpg

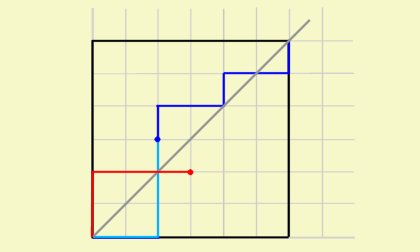
이 때, 이 경로의 \((0,0)\)에서부터 \(y=x+1\)과 처음으로 만나는 점까지를 잘라서, \(y=x\)에 대칭시키자.

카탈란 수열(Catalan numbers)Symmetrization.jpg

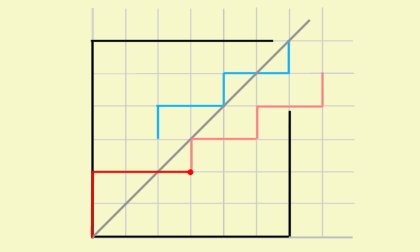
그리고 나머지 경로를 평행이동시켜 대칭이동된 경로에 갖다붙이자.

카탈란 수열(Catalan numbers)translation.jpg

그 결과는 \((0,0)\)에서 출발하여 \((n+1,n-1)\)에 도착하는 경로일 것이다.

카탈란 수열(Catalan numbers)result.jpg

위에서 한 작업은 서로 다른 두 경로의 집합 사이에 어떤 대응을 만들어 낸 것이다. 이 대응은 일대일 대응이다. 일대일대응임을 보이기 위해서는 두 가지를 생각해야 한다. 첫번째는, 서로 다른 것으로 대응되었는지를 살피고, 두번째는 공역의 모든 원소가 대응되었는지를 살피는 것이다.

\(y=x\)를 넘어서서 가는 경로는 \((0,0)\)에서 \((n+1,n-1)\)까지 가는 경로와 일대일 대응되므로 그 개수는 \({2n \choose n+1}\)이다.

따라서 처음에 제기했던 문제의 답은 다음과 같다 \[{2n \choose n}-{2n \choose n+1}=\frac{1}{n+1}{2n \choose n}\] ■




적분표현

  • \(c_n=\int_{0}^{1} 2^{2n+1}{\cos^{2n} \pi x}\, {\sin^2 \pi x}\,dx\)


역사



메모


관련된 항목들


매스매티카 파일 및 계산 리소스


사전 형태의 자료


리뷰, 에세이, 강의노트


관련도서

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'catalan'}, {'LEMMA': 'number'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=카탈란_수_(Catalan_numbers)&oldid=52488"