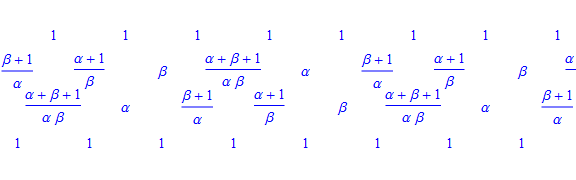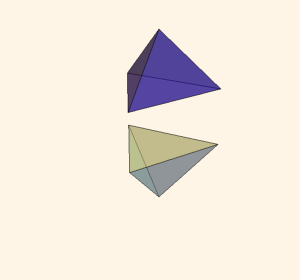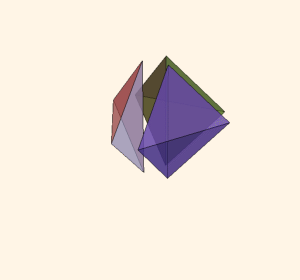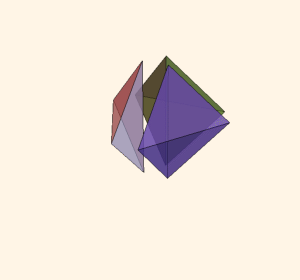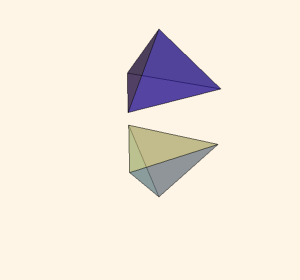5항 관계식 (5-term relation)
개요
- 다이로그 함수(dilogarithm) 가 만족시키는 중요한 항등식
- 함수 다이로그 항등식(functional dilogarithm identity) 으로 일반화됨
로저스 다이로그 함수
- \(x\in (0,1)\)일 때, 로저스 다이로그 함수 (Rogers' dilogarithm) 를 다음과 같이 정의
\[L(x)=\operatorname{Li}_ 2(x)+\frac{1}{2}\log x\log (1-x)=-\frac{1}{2}\int_{0}^{x}\left(\frac{\log(1-y)}{y}+\frac{\log(y)}{1-y}\right)dy\]
5항 관계식
- 로저스 다이로그 함수 \(L(x)\)
- \(0\leq x,y\leq 1\) 일 때, 다음이 성립한다
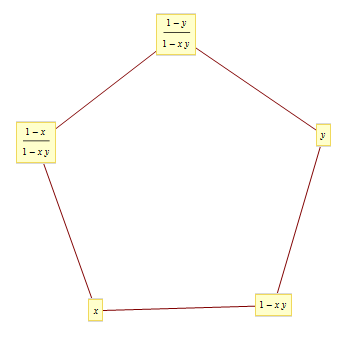
\[L(x)+L(1-xy)+L(y)+L\left(\frac{1-y}{1-xy}\right)+L\left(\frac{1-x}{1-xy} \right)=\frac{\pi^2}{2}\]
- \(1-x_{i}=x_{i-1}x_{i+1}\), \(x_0=x\), \(x_2=y\)로 정의되는 점화식은 주기가 5인 수열이 된다\[x_0=x, x_1=1-xy, x_2=y, x_3=\frac{1-y}{1-xy}, x_4=\frac{1-x}{1-xy}\]
- 이 수열은 Lyness 차분방정식 이라는 이름으로 연구되기도 하였음
- 집합 \(\{0,1,\infty,y,xy\}\) 에서 4개의 원소를 뽑아 얻어지는 교차비(cross ratio)
q-이항정리를 통한 증명
- [GM1997]참고
- q-이항정리\[\sum_{n=0}^{\infty} \frac{(a;q)_n}{(q;q)_n}b^n=\frac{(ab;q)_{\infty}}{(b;q)_{\infty}}\]
- z를 \((1-az)b=1-z\) 의 해로 정의, 즉\[z=\frac{1-b}{1-ab}\]
- \(q=e^{-t}\)이고 t가 0으로 갈 때, 양변의 근사식은 다음과 같다 좌변 \(\frac{\operatorname{Li}_2(az)-\operatorname{Li}_2(a)-\operatorname{Li}_2(z)+\operatorname{Li}_2(1)-\log z\log b}{t}\) 우변 \(\frac{\operatorname{Li}_2(b)-\operatorname{Li}_2(ab)}{t}\)
- 양변의 근사식을 비교하여 5항 관계식을 얻는다 \[\operatorname{Li}_2(az)-\operatorname{Li}_2(a)-\operatorname{Li}_2(z)+\operatorname{Li}_2(1)-\log z\log b=\operatorname{Li}_2(b)-\operatorname{Li}_2(ab)\]
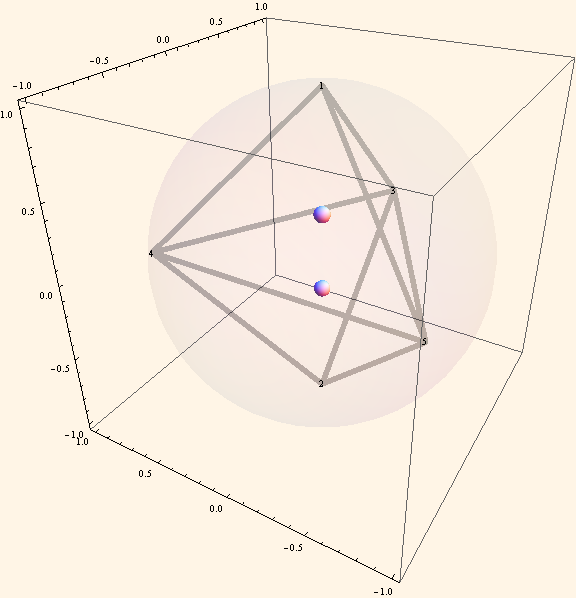
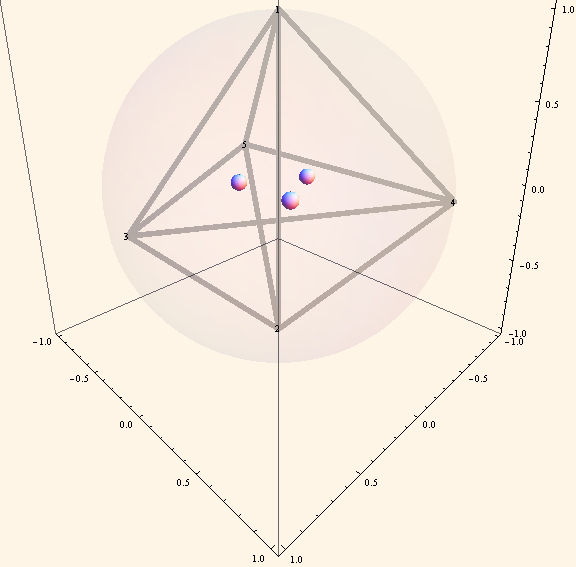
Pachner Move
- 사면체 두 개를 붙여 얻어진 다면체를 세 개의 사면체로 쪼개는 방법
- 쌍곡 3차원 다양체에 이를 적용하면, 다이로그 함수의 5항 관계식을 얻는다
재미있는 사실
" I like explicit, hands-on formulas. To me they have a beauty of their own. They can be deep or not. As an example, imagine you have a series of numbers such that if you add 1 to any number you will get the product of its left and right neighbors. Then this series will repeat itself at every fifth step! For instance, if you start with 3, 4 then the sequence continues: 3, 4, 5/3, 2/3, 1, 3, 4, 5/3, etc. The difference between a mathematician and a nonmathematician is not just being able to discover something like this, but to care about it and to be curious about why it's true, what it means, and what other things in mathematics it might be connected with. In this particular case, the statement itself turns out to be connected with a myriad of deep topics in advanced mathematics: hyperbolic geometry, algebraic K-theory, the Schrodinger equation of quantum mechanics, and certain models of quantum field theory. I find this kind of connection between very elementary and very deep mathematics overwhelmingly beautiful." Don Zagier (Mathematicians: An Outer View of the Inner World):
- Doliwa, Adam, and Sergey M. Sergeev. “The Pentagon Relation and Incidence Geometry.” arXiv:1108.0944 [math-Ph, Physics:nlin], August 3, 2011. http://arxiv.org/abs/1108.0944.
역사
메모
관련된 항목들
매스매티카 파일 및 계산 리소스
사전 형태의 자료
리뷰논문, 에세이, 강의노트
- Gregory Leibon, Scissors Congruence : The Birth of Hyperbolic Volume
관련논문
- Adriano Garsia, Anton Mellit, Five-term relation and Macdonald polynomials, arXiv:1604.08655 [math.CO], April 29 2016, http://arxiv.org/abs/1604.08655
- Gahramanov, Ilmar, and Hjalmar Rosengren. “Integral Pentagon Relations for 3d Superconformal Indices.” arXiv:1412.2926 [hep-Th, Physics:math-Ph], December 9, 2014. http://arxiv.org/abs/1412.2926.
- Faddeev, L. D. 2012. “Volkov’s Pentagon for the Modular Quantum Dilogarithm.” arXiv:1201.6464 (January 31). http://arxiv.org/abs/1201.6464.
- Kashaev, R. M. 2004. “The Q-binomial Formula and the Rogers Dilogarithm Identity”. ArXiv e-print math/0407078. http://arxiv.org/abs/math/0407078.
- [GM1997] Gordon, Basil, and Richard J. Mcintosh. 1997. “Algebraic Dilogarithm Identities.” The Ramanujan Journal 1 (4) (December 1): 431–448. doi:10.1023/A:1009709927327.
- Zdzisław Wojtkowiak, Functional equations of iterated integrals with regular singularities, Nagoya Math. J. Volume 142 (1996), 145-159. http://projecteuclid.org/euclid.nmj/1118772047
- Moak, Daniel S. 1984. “The \(q\)-analogue of Stirling’s formula”. The Rocky Mountain Journal of Mathematics 14 (2): 403–413. doi:10.1216/RMJ-1984-14-2-403.
- N. H. Abel, Note sur la fonction \(\psi x=x+\frac{x^2}{2^2}+\frac{x^3}{3^2}+\cdots\), Oeuvres complètes de Niels Hendrik Abel, Tome second, Christiania 1881; reprinted by Johnson Reprint Corp., New York, 1973, pp. 189-193. http://www.abelprisen.no/nedlastning/verker/oeuvres_1881_del2/oeuvres_completes_de_abel_nouv_ed_2_kap14_opt.pdf