황금비

황금비

• \(\varphi=\frac{1+\sqrt5}{2}=1.61803398874989\cdots\)
• 두 수 (또는 길이) \(a,b\)가 \(a+b:a=a:b\) 를 만족시키면 황금비를 이룬다고 말함

[[Media:|Media:]]

정오각형과 황금비

• 정오각형의 한 변의 길이와 대각선의 길이의 비율은 황금비가 된다.

\({b \over a}={{(1+\sqrt{5})}\over 2}\)

• 정오각형

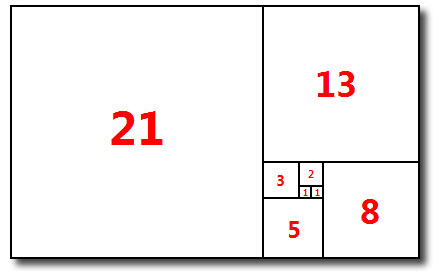
황금비와 피보나치 수열

• 피보나치 수열의 여러가지 성질

황금비와 정이십면체

Golden rectangles in an icosahedron

• 황금사각형 세 개가 이루는 꼭지점이 정이십면체의 꼭지점이 된다

연분수

\(\frac{1+\sqrt5}{2}=1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}\)

유리수 근사와 황금비

무리수 \(\alpha\) 에 대하여,

\(|\frac{p}{q}-\alpha|<\frac{1}{\sqrt{5}{q^2}}\)

는 무한히 많은 p,q 에 의하여 만족된다. 하지만 여기서 \(\sqrt{5}\) 는 더 큰 수로 대체될 수 없다.

• 연분수 항목을 참조

로저스-라마누잔 연분수

\(\cfrac{1}{1 + \cfrac{e^{-2\pi}}{1 + \cfrac{e^{-4\pi}}{1+\dots}}} = \left({\sqrt{5+\sqrt{5}\over 2}-{\sqrt{5}+1\over 2}}\right)e^{2\pi/5} = e^{2\pi/5}\left({\sqrt{\varphi\sqrt{5}}-\varphi}\right) = 0.9981360\dots\)

• 라마누잔의 연분수

Dilogarithm

\(\mbox{Li}_{2}(\frac{3-\sqrt{5}}{2})=\frac{\pi^2}{15}-\log^2(\frac{1+\sqrt{5}}{2})\)

\(\mbox{Li}_{2}(\frac{-1+\sqrt{5}}{2})=\frac{\pi^2}{10}-\log^2(\frac{1+\sqrt{5}}{2})\)

\(\mbox{Li}_{2}(\frac{1-\sqrt{5}}{2})=-\frac{\pi^2}{15}+\frac{1}{2}\log^2(\frac{1+\sqrt{5}}{2})\)

\(\mbox{Li}_{2}(\frac{-1-\sqrt{5}}{2})=-\frac{\pi^2}{10}+\frac{1}{2}\log^2(\frac{1+\sqrt{5}}{2})\)

• Dilogarithm 항목을 참조

르장드르 카이 함수

• 르장드르 카이 함수

\[\chi_2(\frac{\sqrt{5} -1}{2}) = \frac{\pi^2}{12}-\frac{3}{4}\ln^2(\frac{\sqrt{5}+1}{2})\] \[\chi_2(\sqrt{5} -2) = \frac{\pi^2}{24}-\frac{3}{4}\ln^2(\frac{\sqrt{5}+1}{2})\]

메모

• golden integral : http://www.mathlinks.ro/Forum/viewtopic.php?p=785258#785258
• 숫자 5 http://plus.maths.org/issue45/features/kaplan/index.html
• This Week's Finds in Mathematical Physics (Week 203)
  • John Baez
• Misconceptions about the Golden Ratio
  • George Markowsky
  • The College Mathematics Journal, Vol. 23, No. 1 (Jan., 1992), pp. 2-19

관련된 항목들

• 정오각형
• 정다면체
• 피보나치 수열의 여러가지 성질
• Dilogarithm
• 라마누잔의 연분수

사전형태의 자료

• http://ko.wikipedia.org/wiki/황금비
• http://en.wikipedia.org/wiki/golden_ratio
• http://www18.wolframalpha.com/input/?i=golden+ratio

동영상

• Nature by Numbers
• http://www.youtube.com/results?search_type=&search_query=

메타데이터

위키데이터

• ID : Q41690

Spacy 패턴 목록

• [{'LOWER': 'golden'}, {'LEMMA': 'ratio'}]
• [{'LEMMA': 'φ'}]
• [{'LEMMA': 'φ'}]
• [{'LEMMA': 'Τ'}]
• [{'LEMMA': 'τ'}]
• [{'LEMMA': 'Phi'}]
• [{'LEMMA': 'Tau'}]
• [{'LOWER': 'golden'}, {'LEMMA': 'mean'}]
• [{'LOWER': 'golden'}, {'LEMMA': 'section'}]