"톨레미의 정리"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
|||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| + | * 원에 내접하는 사각형의 변의 길이 사이의 관계 | ||
| − | + | [[Image:톨레미.png|500px]] | |
| − | + | ||
| − | + | ==내접사각형에 대한 톨레미의 정리== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
: | : | ||
| 27번째 줄: | 18번째 줄: | ||
| − | + | ||
| − | + | ==삼각함수 덧셈공식의 유도== | |
[/pages/3324857/attachments/4590231 sin_cosine3.gif] | [/pages/3324857/attachments/4590231 sin_cosine3.gif] | ||
| 36번째 줄: | 27번째 줄: | ||
* [[삼각함수]] | * [[삼각함수]] | ||
| − | + | ||
| − | + | ||
| − | + | ==메모== | |
* [http://www.maths.gla.ac.uk/%7Ewws/cabripages/hyperbolic/ptolemyproof.html http://www.maths.gla.ac.uk/~wws/cabripages/hyperbolic/ptolemyproof.html] | * [http://www.maths.gla.ac.uk/%7Ewws/cabripages/hyperbolic/ptolemyproof.html http://www.maths.gla.ac.uk/~wws/cabripages/hyperbolic/ptolemyproof.html] | ||
* An analogue of Ptolemy's theorem and its converse in hyperbolic geometry. http://goo.gl/iupfB | * An analogue of Ptolemy's theorem and its converse in hyperbolic geometry. http://goo.gl/iupfB | ||
| − | + | ||
| − | + | ==재미있는 사실== | |
* 톨레미 알마게스트의 사인표(정확히는 현의 길이) 계산에 이용됨 | * 톨레미 알마게스트의 사인표(정확히는 현의 길이) 계산에 이용됨 | ||
| − | + | ||
| − | + | ||
| − | + | ==관련된 항목들== | |
* [[정다각형의 대각선의 길이]] | * [[정다각형의 대각선의 길이]] | ||
| 63번째 줄: | 54번째 줄: | ||
* [[수학사연표 (역사)|수학사연표]] | * [[수학사연표 (역사)|수학사연표]] | ||
| − | + | ||
| − | + | ||
| − | + | ==사전형태의 자료== | |
* http://ko.wikipedia.org/wiki/ | * http://ko.wikipedia.org/wiki/ | ||
* http://en.wikipedia.org/wiki/Ptolemy%27s_theorem | * http://en.wikipedia.org/wiki/Ptolemy%27s_theorem | ||
| − | + | ||
| − | + | ==관련도서== | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==관련논문== | |
| − | + | * Guo, Ren, and Nilgün Sönmez. 2010. Cyclic polygons in classical geometry. 1009.2970 (September 15). http://arxiv.org/abs/1009.2970. | |
| − | + | * Apostol, Tom M. 1967. Ptolemy's Inequality and the Chordal Metric. Mathematics Magazine 40, no. 5 (November 1): 233-235. doi:[http://dx.doi.org/10.2307/2688275 10.2307/2688275]. | |
| − | * Guo, Ren, and Nilgün Sönmez. 2010. Cyclic polygons in classical geometry. 1009.2970 (September 15). http://arxiv.org/abs/1009.2970. | ||
| − | * Apostol, Tom M. 1967. Ptolemy's Inequality and the Chordal Metric. Mathematics Magazine 40, no. 5 (November 1): 233-235. doi:[http://dx.doi.org/10.2307/2688275 10.2307/2688275]. | ||
* [http://hypertextbook.com/eworld/chords.shtml Ptolemy's Table of Chords Trigonometry in the Second Century] | * [http://hypertextbook.com/eworld/chords.shtml Ptolemy's Table of Chords Trigonometry in the Second Century] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
2012년 9월 16일 (일) 12:42 판
개요
- 원에 내접하는 사각형의 변의 길이 사이의 관계
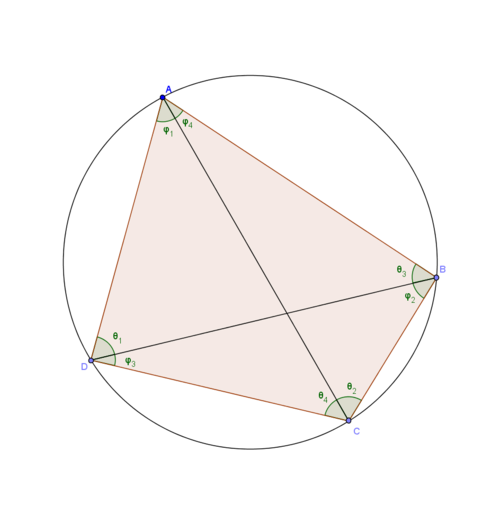
내접사각형에 대한 톨레미의 정리
(정리)
사각형이 원에 내접할때, 두 대각선의 길이의 곱은 서로 마주보고 있는 두 변의 쌍의 길이의 곱의 합과 같다.
\(\overline{AC}\cdot \overline{BD}=\overline{AB}\cdot \overline{CD}+\overline{BC}\cdot \overline{AD}\)
[/pages/3324857/attachments/3540037 PtolemyQD.jpg]
삼각함수 덧셈공식의 유도
[/pages/3324857/attachments/4590231 sin_cosine3.gif]
메모
- http://www.maths.gla.ac.uk/~wws/cabripages/hyperbolic/ptolemyproof.html
- An analogue of Ptolemy's theorem and its converse in hyperbolic geometry. http://goo.gl/iupfB
재미있는 사실
- 톨레미 알마게스트의 사인표(정확히는 현의 길이) 계산에 이용됨
관련된 항목들
사전형태의 자료
관련도서
관련논문
- Guo, Ren, and Nilgün Sönmez. 2010. Cyclic polygons in classical geometry. 1009.2970 (September 15). http://arxiv.org/abs/1009.2970.
- Apostol, Tom M. 1967. Ptolemy's Inequality and the Chordal Metric. Mathematics Magazine 40, no. 5 (November 1): 233-235. doi:10.2307/2688275.
- Ptolemy's Table of Chords Trigonometry in the Second Century