정다각형의 대각선의 길이

수학노트
둘러보기로 이동 검색으로 이동

개요

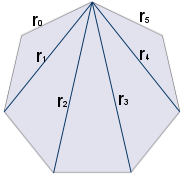
  • 한 변의 길이가 1인 정n각형의 대각선의 길이
  • 편의상 <math>n=\ell+2</math>로 두자. 대각선의 길이 <math>r_i</math>는 다음과 같이 주어진다
<math>r_i=\frac{\sin \left(\frac{\pi (i+1)}{\ell+2}\right)}{\sin \left(\frac{\pi }{\ell+2}\right)},\quad i=0,1,\cdots,\ell</math>

6782509-heptagon.png


대각선이 만족시키는 항등식 1

  • 다음을 만족한다
<math>r_h\times r_k=r_{h-k}+r_{h-k+2}+\cdots+r_{h+k} \label{pd}</math>

여기서 <math>0\leq k\leq h<n/2</math>이고, 우변은 k+1개항의 합.

  • 다음과 같이 쓸 수 있다
<math>

r_{h}\times r_{k}= r_{|h-k|}+ r_{|h-k|+2}+ \cdots + r_{\operatorname{min}(2\ell-(h+k),h+k)} </math> 여기서 <math>0\leq h,k \leq \ell</math>

  • 고등수학의 등각장론에서 fusion rule 로 등장한다


증명

다음과 같은 삼각함수의 덧셈과 곱셈 공식 을 이용하자.

<math>\sin{x} \sin{y} = -{\cos(x + y) - \cos(x - y) \over 2}</math>

이를 이용하여, 다음을 얻을 수 있다

<math>\sin \frac{(h+1)\pi}{n}\sin \frac{(k+1)\pi}{n}=\sum_{j=0}^{k}\sin \frac{(h-k+2j+1)\pi}{n}\sin \frac{\pi}{n}</math>

따라서

<math>r_h\times r_k=r_{h-k}+r_{h-k+2}+\cdots+r_{h+k}</math> ■


대각선이 만족시키는 항등식 2

  • <math>r_i</math>는 다음의 점화식을 만족한다
<math>r_i^2=1+r_{i-1}r_{i+1}, 1\leq i \leq \ell-1</math>
  • \ref{pd}을 이용하여 증명할 수 있다
  • 이는 제2종 체비셰프 다항식이 만족시키는 항등식 <math>U_n(x)^2=1+U_{n-1}(x)U_{n+1}(x)</math>과 같다


양자미적분학

  • q-초기하급수(q-hypergeometric series)와 양자미적분학(q-calculus) 에서 실수 n 의 q-analogue 로:<math>[n]_q =\frac{q^{n}-q^{-n}}{q-q^{-1}} </math> 와 같은 표현을 사용하기도 함
  • <math>q=e^{i\theta}</math> 로 두면,:<math>[n]_q =\frac{e^{in\theta}-e^{-in\theta}}{e^{i\theta}-e^{-i\theta}} =\frac{\sin n\theta}{\sin \theta}</math> 를 얻는다
  • 정다각형의 대각선의 길이:<math>r_i=\frac{\sin \left(\frac{\pi (i+1)}{n}\right)}{\sin \left(\frac{\pi }{n}\right)}</math> 와 유사한 표현을 얻는다
  • 이는 바일 차원 공식(Weyl dimension formula)을 이용하여 quantum dimension을 정의할 때 등장하는 표현이다


예

정사각형의 대각선


정사각형의 대각선의 길이

한변의 길이가 1인 정사각형의 대각선의 길이는 피타고라스의 정리를 이용하여 루트 2가 됨을 보일수 있다. "루트2는 무리수" 라는 이야기는 중고교수학에서 배우는 가장 멋진 사실의 하나라 할 수 있다.



정오각형의 대각선

방법1

정오각형의 한 변의 길이와 대각선의 길이의 비율이 황금비가 된다는 것은 잘 알려진 사실이다.

<math>{b \over a}={{(1+\sqrt{5})}\over 2}</math>

3002548-pentagon(1).png

정오각형의 한 변의 길이가 1인 경우, 즉 <math>a=1</math>인 경우에 b는 황금비가 된다.

증명

삼각형 ABD에서 선분 AC는 각 A의 이등분선이다. (각 DAC와 각 CAB가 같은 길이를 갖는 두 현 DC와 BC의 원주각이기 때문)

AC와 BD의 교점을 E라 하자.

각의 이등분선의 성질에 의해,

AB : AD = BE : DE 즉 <math>a : b = b-a : a</math> 가 성립한다.

<math>b^2 - ab - a^2 = 0</math>
<math>(\frac{b}{a})^2- \frac{b}{a} - 1 =0</math>

■


방법 2

정오각형의 대각선의 길이를 구하는 또 다른 방법의 하나는 평면기하의 톨레미의 정리를 이용하는 것이다. 톨레미의 정리는 다음과 같다 :

사각형이 원에 내접할때, 두 대각선의 길이의 곱은 서로 마주보고 있는 두 변의 쌍의 길이의 곱의 합과 같다.

즉, 아래그림에서 <math>\overline{AC}\cdot \overline{BD}=\overline{AB}\cdot \overline{CD}+\overline{BC}\cdot \overline{AD}</math> 이 성립한다.


3002548-pentagon(1).png


톨레미의 정리를 적용해 보면, 사각형 ABCD가 원에 내접하고 있으므로, 두 대각선 AC와 BD의 길이의 곱으로부터 <math>\overline{AC}\cdot \overline{BD}=b^2</math>을 얻고, <math>\overline{AB}\cdot \overline{CD}+\overline{BC}\cdot \overline{AD}=a^2+ab</math>를 얻을 수 있다.

이로부터 <math>b^2 - ab - a^2 = 0</math>를 얻을 수도 있다.

정육각형의 대각선

정육각형의 대각선의 길이

각 변의 길이가 1인 정육각형의 대각선의 길이는 <math>\sqrt{3}</math>과 2가 되는데, 이는 정삼각형의 변의 길이를 구할 수 있다면 어렵지 않게 구할 수 있다.



정칠각형의 대각선


정칠각형의 대각선의 길이

정칠각형의 대각선의 길이도 마찬가지로 톨레미의 정리를 여러번 적용하면 구할 수 있다.

6782509-heptagon.png

한변의 길이 <math>r_0=1</math> 라 두고, 톨레미의 정리를 적용하면,

<math>r_1^2=1+r_2</math>

<math>r_2r_1=r_1+r_2</math>

<math>r_2^2=r_2r_1+1</math>

와 같은 관계를 얻을 수 있다.


이를 이용하면, 다음과 같은 사실들을 알 수 있다.

<math>r_1</math>은 <math>x^3-x^2-2x+1=0</math> 의 해이고, <math>r_2</math>은 <math>x^3-2x^2-x+1=0</math> 의 해이다.

(증명)

<math>r_2=r_1^2-1</math> 이므로, <math>r_2r_1=r_1+r_2</math>로부터 <math>r_1(r_1^2-1)=r_1+r_1^2-1</math>.

<math>r_2^2=r_2r_1+1=r_1+r_2+1</math> 이므로, <math>r_1=r_2^2-r_2-1</math>. 이제 <math>r_2r_1=r_1+r_2</math>로부터, <math>r_2(r_2^2-r_2-1)=r_2^2-r_2-1+r_2</math>. ■

이제 3차 방정식을 풀면 된다.


메모



관련된 항목들


관련논문


매스매티카 파일 및 계산 리소스

원본 주소 "https://wiki.mathnt.net/index.php?title=정다각형의_대각선의_길이&oldid=38694"