"Nested radicals"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| 62번째 줄: | 62번째 줄: | ||
| + | ==함수방정식== | ||
| + | * $f(x)=\sqrt{1+x \sqrt{1+(x+1) \sqrt{1+(x+2) \sqrt{\cdots}}}}$ | ||
| + | * $[f(x)]^2=1+xf(x+1)$ | ||
| + | * Functional Equations and and How to Solve Them Section 3.8 Functional equations and nested radicals | ||
| 82번째 줄: | 86번째 줄: | ||
| − | == | + | ==관련도서== |
| − | |||
* Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000. | * Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000. | ||
| + | * Functional Equations and and How to Solve Them | ||
| + | ** section 3.8 | ||
2012년 12월 25일 (화) 15:18 판
이 항목의 스프링노트 원문주소
개요
- 황금비
\(\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}}=\varphi=\frac{1+\sqrt5}{2}=1.61803398874989\cdots\) - 비에타의 공식
\(\frac{2}{\pi}=\frac{\sqrt{2}}{2}\frac{\sqrt{2+\sqrt{2}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}}{2}\cdots\) - nested radical 상수
\(\sqrt{1+\sqrt{2+\sqrt{3+\sqrt{4+\sqrt{5+\sqrt{6+\cdots}}}}}}=1.75793275661800453270881963821820816125\cdots\) - 삼각함수의 값
\(\cos \frac{\pi}{32}=\cos\frac{\pi}{2^5}= \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2}\)
\(\cos \frac{\pi}{64}=\cos\frac{\pi}{2^6}= \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}{2}\)
라마누잔이 제시한 문제
- \(\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+5\sqrt{1+6\cdots}}}}} = 3\)
- 다음 수열의 극한
\(1,\sqrt{1+2 },\sqrt{1+2 \sqrt{1+3 }},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 }}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 }}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 }}}}}, \cdots\)
증명
먼저 수렴성을 증명하자. 다음과 같이 정의된 수열
\(1,\sqrt{1+2 },\sqrt{1+2 \sqrt{1+3 }},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 }}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 }}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 }}}}}, \cdots\) 은 위로 유계이다.
\(\sqrt{1+2 \sqrt{1+3\sqrt{1+\cdots+ (n-1)\sqrt{1+n} }}} \leq \sqrt{1+2 \sqrt{1+3\sqrt{1+\cdots+ (n-1)\sqrt{1+n(n+2)} }}}=3\)
\(n=\sqrt{1+(n-1)(n+1)}\)을 이용
\(\begin{eqnarray*}3 &=& \sqrt{1+2\cdot4}\\ &=& \sqrt{1+2\sqrt{1+3\cdot5}}\\ &=& \sqrt{1+2\sqrt{1+3\sqrt{1+4\cdot6}}}\\ &=& \cdots\end{eqnarray*}\)
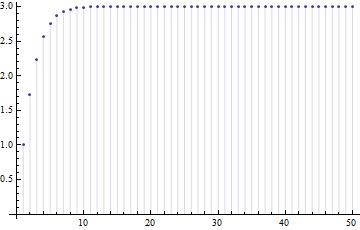
수열의 크기 변화를 나타내는 그래프
\(1,\sqrt{1+2 },\sqrt{1+2 \sqrt{1+3 }},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 }}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 }}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 }}}}}, \cdots\)
매쓰매티카 코드
- f[n_][x_]:=Sqrt[1+n*x]
a[1][x_]:=x
a[n_][x_]:=Composition[a[n-1],f[n]][x]
Table[a[n][x],{n,1,6}]
DiscretePlot[a[n][1],{n,1,50}]
- 결과
\(\left\{x,\sqrt{1+2 x},\sqrt{1+2 \sqrt{1+3 x}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 x}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 x}}}},\sqrt{1+2 \sqrt{1+3 \sqrt{1+4 \sqrt{1+5 \sqrt{1+6 x}}}}}\right\}\)
함수방정식
- $f(x)=\sqrt{1+x \sqrt{1+(x+1) \sqrt{1+(x+2) \sqrt{\cdots}}}}$
- $[f(x)]^2=1+xf(x+1)$
- Functional Equations and and How to Solve Them Section 3.8 Functional equations and nested radicals
메모
- http://www.dgp.toronto.edu/~mjmcguff/math/nestedRadicals.pdf
- http://fluxionsdividebyzero.com/p1/math/calculus/number/cr/sr_nroots.pdf
관련된 항목들
관련도서
- Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000.
- Functional Equations and and How to Solve Them
- section 3.8
관련논문
- Ramanujan, S. Question No. 298. J. Indian Math. Soc. 1911.
사전형태의 참고자료