"리대수 sl(4,C)의 유한차원 표현론"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) (새 문서: ==개요== * 복소수체 위의 15차원 리대수 $\mathfrak{g}=\mathfrak{sl}(4,\mathbb{C})$ * $\mathfrak{g}=\{X\in \mathfrak{gl}(4,\mathbb{C})|\operatorname{Tr}(X)=0 \}$ * $A_3$ ...) |
Pythagoras0 (토론 | 기여) |
||
| 118번째 줄: | 118번째 줄: | ||
** <math>\alpha_2=(0,1,-1,0)</math> | ** <math>\alpha_2=(0,1,-1,0)</math> | ||
** <math>\alpha_3=(0,0,1,-1)</math> | ** <math>\alpha_3=(0,0,1,-1)</math> | ||
| + | [[파일:리대수 sl(4,C)의 유한차원 표현론1.png]] | ||
* fundamental weights | * fundamental weights | ||
** $\omega_1=(3/4, -(1/4), -(1/4), -(1/4))$ | ** $\omega_1=(3/4, -(1/4), -(1/4), -(1/4))$ | ||
| 147번째 줄: | 148번째 줄: | ||
\chi_{\omega_1}=x_1+\frac{x_2}{x_1}+\frac{1}{x_3}+\frac{x_3}{x_2} | \chi_{\omega_1}=x_1+\frac{x_2}{x_1}+\frac{1}{x_3}+\frac{x_3}{x_2} | ||
$$ | $$ | ||
| + | * weight diagram | ||
| + | [[파일:리대수 sl(4,C)의 유한차원 표현론2.png]] | ||
| + | |||
===예2=== | ===예2=== | ||
| 155번째 줄: | 159번째 줄: | ||
\chi_{\omega_1+\omega_3}=3+\frac{x_1^2}{x_2}+\frac{x_2}{x_1^2}+\frac{x_2}{x_3^2}+\frac{1}{x_1 x_3}+\frac{x_1}{x_2 x_3}+\frac{x_1 x_2}{x_3}+\frac{x_2^2}{x_1 x_3}+x_1 x_3+\frac{x_1 x_3}{x_2^2}+\frac{x_3}{x_1 x_2}+\frac{x_2 x_3}{x_1}+\frac{x_3^2}{x_2} | \chi_{\omega_1+\omega_3}=3+\frac{x_1^2}{x_2}+\frac{x_2}{x_1^2}+\frac{x_2}{x_3^2}+\frac{1}{x_1 x_3}+\frac{x_1}{x_2 x_3}+\frac{x_1 x_2}{x_3}+\frac{x_2^2}{x_1 x_3}+x_1 x_3+\frac{x_1 x_3}{x_2^2}+\frac{x_3}{x_1 x_2}+\frac{x_2 x_3}{x_1}+\frac{x_3^2}{x_2} | ||
$$ | $$ | ||
| + | * weight diagram | ||
| + | [[파일:리대수 sl(4,C)의 유한차원 표현론3.png]] | ||
| + | |||
| + | |||
| + | ===예3=== | ||
| + | * highest weight $\omega_1+\omega_2+\omega_3$ | ||
| + | * 64차원 표현 | ||
| + | * weight diagram | ||
| + | [[파일:리대수 sl(4,C)의 유한차원 표현론4.png]] | ||
| + | |||
==관련된 항목들== | ==관련된 항목들== | ||
2014년 2월 4일 (화) 22:06 판
개요
- 복소수체 위의 15차원 리대수 $\mathfrak{g}=\mathfrak{sl}(4,\mathbb{C})$
- $\mathfrak{g}=\{X\in \mathfrak{gl}(4,\mathbb{C})|\operatorname{Tr}(X)=0 \}$
- $A_3$ 타입의 단순 리대수
리대수 $\mathfrak{sl}(4,\mathbb{C})$
- 기저
$$ \begin{array}{|rcl|} \hline h_1 & = & \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \hline h_2 & = & \left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \hline h_3 & = & \left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{array} \right) \\ \hline e_1 & = & \left( \begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \hline e_2 & = & \left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \hline e_3 & = & \left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \hline e_4 & = & \left( \begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \hline e_5 & = & \left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \hline e_6 & = & \left( \begin{array}{cccc} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \hline f_i & = & e_i^t,\quad 1\leq i\leq 6 \\ \hline \end{array} $$
- $A_3$ 카르탄 행렬
\[A=\left( \begin{array}{ccc} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{array} \right)\]
- $A_3$ 루트 시스템
\[\Phi=\left\{ \alpha _1,\alpha _2,\alpha _3,\alpha _1+\alpha _2,\alpha _2+\alpha _3,\alpha _1+\alpha _2+\alpha _3,\\ -\alpha _1,-\alpha _2,-\alpha _3,-\alpha _1-\alpha _2,-\alpha _2-\alpha _3,-\alpha _1-\alpha _2-\alpha _3 \right \}\]
- 바일군
$$\{s[],s[1],s[2],s[3],s[1,2],s[1,3],s[2,1],s[2,3],s[3,2],\\ s[1,2,1],s[1,2,3],s[1,3,2],s[2,1,3],s[2,3,2],s[3,2,1],\\ s[1,2,1,3],s[1,2,3,2],s[1,3,2,1],s[2,1,3,2],s[2,3,2,1],s[1,2,1,3,2],s[1,2,3,2,1],s[2,1,3,2,1],s[1,2,1,3,2,1]\} $$
- \(A_3\)의 루트 시스템을 \(\mathbb{R}^4\)안에서 다음과 같이 얻을 수 있다
- \(\alpha_1=(1,-1,0,0)\)
- \(\alpha_2=(0,1,-1,0)\)
- \(\alpha_3=(0,0,1,-1)\)
- fundamental weights
- $\omega_1=(3/4, -(1/4), -(1/4), -(1/4))$
- $\omega_2=(1/2, 1/2, -(1/2), -(1/2))$
- $\omega_3=(1/4, 1/4, 1/4, -(3/4))$
- 바일 벡터 \(\rho=(3/2, 1/2, -(1/2), -(3/2))\)
유한차원 기약 표현의 분류
- 유한차원 기약 표현 $V$에 대하여, 적당한 dominant weight $\omega=a\omega_1+b\omega_2+c\omega_3,\quad a,b,c\in \mathbb{Z}_{\geq 0}$가 존재하여, $V\cong L(\omega)$가 성립
- 바일 차원 공식(Weyl dimension formula)을 이용하면, 다음을 얻는다
$$ \dim L(a\omega_1+b\omega_2+c\omega_3)=\frac{1}{12} (a+1) (b+1) (c+1) (a+b+2) (b+c+2) (a+b+c+3) $$
기약표현의 예
- 표현 $V=L(\lambda)$의 지표를 다음과 같이 정의
$$ \chi_{\lambda}=\sum_{\lambda' \in P} (\dim{V_{\lambda'}})e^{\lambda'} $$
- $x_1=e^{\omega_1}, x_2=e^{\omega_2},x_3=e^{\omega_3}$로 두면, $\chi_{\lambda}$는 $\mathbb{Z}[x_1^{\pm},x_2^{\pm},x_3^{\pm}]$의 원소가 된다
- 바일 지표 공식 (Weyl character formula) 항목 참조
예1
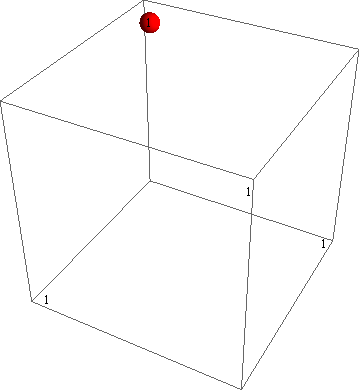
- fundamental 표현, highest weight은 $\omega_1$
- 4차원 표현
- 지표
$$ \chi_{\omega_1}=x_1+\frac{x_2}{x_1}+\frac{1}{x_3}+\frac{x_3}{x_2} $$
- weight diagram
예2
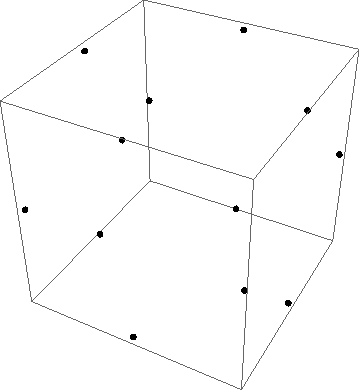
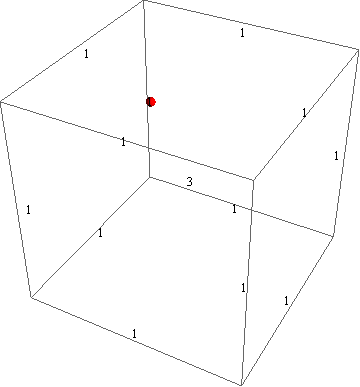
- adjoint 표현, highest weight은 $\omega_1+\omega_3$
- 15차원 표현
- 지표
$$ \chi_{\omega_1+\omega_3}=3+\frac{x_1^2}{x_2}+\frac{x_2}{x_1^2}+\frac{x_2}{x_3^2}+\frac{1}{x_1 x_3}+\frac{x_1}{x_2 x_3}+\frac{x_1 x_2}{x_3}+\frac{x_2^2}{x_1 x_3}+x_1 x_3+\frac{x_1 x_3}{x_2^2}+\frac{x_3}{x_1 x_2}+\frac{x_2 x_3}{x_1}+\frac{x_3^2}{x_2} $$
- weight diagram
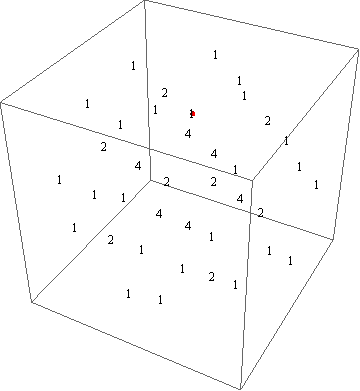
예3
- highest weight $\omega_1+\omega_2+\omega_3$
- 64차원 표현
- weight diagram
관련된 항목들