"뫼비우스의 띠"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
(피타고라스님이 이 페이지에 moeb.gif 파일을 등록하셨습니다.)
 
(사용자 3명의 중간 판 33개는 보이지 않습니다)
1번째 줄: 1번째 줄:
−
<h5>간단한 소개</h5>
+
==개요==
  
−
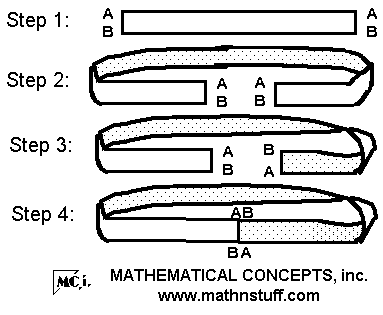
* 사각형 모양의 종이를 하나 가져와서, 왼쪽과 오른쪽 양끝을 서로 붙이되 한번 꼬아서 붙인 것을 뫼비우스의 띠라 함.
+
* 사각형 모양의 띠를 가지고, 왼쪽과 오른쪽 양끝을 서로 붙이되 한번 꼬아서 붙인 것을 뫼비우스의 띠라 함.
−
* 뫼비우스의 띠에서는 곡면의 안과 밖을 구분할 수가 없음.
 
−
* 한 점에서 출발하여 계속 나아가면, 같은 ㅈ
 
  
−
 
+
[[파일:2014134-moeb.gif]]
  
−
<h5>재미있는 사실</h5>
+
*  뫼비우스의 띠에서는 곡면의 안과 밖을 구분할 수가 없음.
 +
** 한 점에서 출발하여 계속 걸어가면, 같은 점에 반대면에 처음에서 거꾸로 선 상태로 도달할수 있고, 계속 걸어간다면, 그 점에 처음 출발할 때의 상태로 돌아올 수 있음.
  
−
 
+
[[파일:2014134-escher-mobius-2.jpg]]
  
−
 
+
수학을 소재로 한 예술작품을 많이 남긴 에셔의 작품
  
−
<h5>관련된 단원</h5>
+
* fiber product
  
−
 
+
  
−
 
+
  
−
<h5>관련된 다른 주제들</h5>
+
==재미있는 사실==
  
−
 
+
* 조세희의 연작 소설 '난장이가 쏘아올린 작은 공'에는 '〈뫼비우스의 띠〉'를 제목으로 하는 이야기가 수록되어 있음.
 +
* 이렇게 돌고도는 뫼비우스 띠의 성질은, 주변에서 흔히 볼 수 있는 재활용 마크의 디자인에 활용되었음.
  
−
 
+
[[파일:2014134-recycle.jpg]]
  
−
<h5>관련도서 및 추천도서</h5>
+
*  직접 뫼비우스의 띠를 만들어 보는 것도 재미있을 것이다. 긴 띠를 한번 꼬아서 풀로 붙이면 된다.
 +
** 뫼비우스 띠 양 모서리의 중점을 이어서 가위로 자르면 재미있는 일이 벌어진다.
 +
** ⅓ 점과 ⅔ 점을 가위로 잘라 보는 것도 괜찮을걸? (※ 잘라 보면 알겠지만, 가위질은 한 번이다.)
 +
*  SK 텔레콤의 T로고는 뫼비우스 띠를 모티브로 삼은 것
 +
** [http://news.naver.com/main/read.nhn?mode=LSD&mid=sec&sid1=105&oid=015&aid=0002058121 [천자칼럼] 뫼비우스의 띠]
 +
***  한국경제, 2009-4-1[[파일:2014134-20080420143114__C9KS1.jpg]]
  
−
 
+
  
−
 
+
*  브라질의 우표[[파일:2014134-Moebius.jpg]]
 +
* 뫼비우스 띠를 이용한 뮤직박스 http://www.youtube.com/watch?v=3iMI_uOM_fY
  
−
<h5>관련된 고교수학 또는 대학수학</h5>
+
  
−
 
+
==역사==
  
−
 
+
*  1858년 뫼비우스가 발견
 +
* [[수학사 연표]]
  
−
<h5>참고할만한 자료</h5>
+
 +
 
 +
 +
 
 +
==관련된 고교수학 또는 대학수학==
 +
 
 +
* [[대수적위상수학]] (대학수학)
 +
 
 +
 +
 
 +
 +
 
 +
==관련된 항목들==
 +
 
 +
* [[클라인씨의 병(Klein bottle)|클라인씨의 병]]
 +
* [[뫼비우스 변환군과 기하학]]
 +
 
 +
 +
 
 +
 +
 
 +
==관련도서==
 +
 
 +
* [http://book.daum.net/search/contentSearch.do?query=%EB%AB%BC%EB%B9%84%EC%9A%B0%EC%8A%A4%EC%9D%98%EB%9D%A0 http://book.daum.net/search/contentSearch.do?query=뫼비우스의띠]
 +
 
 +
 +
 
 +
 +
 
 +
==사전형태의 자료==
 +
 
 +
* [http://en.wikipedia.org/wiki/M%C3%B6bius_strip http://en.wikipedia.org/wiki/Möbius_strip]
 +
* http://en.wikipedia.org/wiki/Recycling_symbol
 +
 
 +
 +
 
 +
==리뷰, 에세이, 강의노트==
 +
* http://navercast.naver.com/science/math/3630
 +
 
 +
 +
 
 +
==관련기사==
 +
 
 +
* [http://biz.chosun.com/site/data/html_dir/2010/12/22/2010122201900.html 분자 크기 세계에서 뫼비우스 띠 만들어]
 +
* [http://newscenter.lbl.gov/feature-stories/2010/12/20/mobius-symmetry-in-metamaterials/ Strange New Twist: Berkeley Researchers Discover Möbius Symmetry in Metamaterials]
 +
* [http://news.khan.co.kr/section/khan_art_view.html?mode=view&artid=200709181000041&code=900314 [예술속 수학이야기](35) ‘난쏘공’ 에 등장하는 ‘뫼비우스의 띠’]
 +
**  강문봉, 2007-9-18
 +
 
 +
 
 +
[[분류:중학수학]]
 +
 
 +
==메타데이터==
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q226843 Q226843]
 +
===Spacy 패턴 목록===
 +
* [{'LOWER': 'möbius'}, {'LEMMA': 'strip'}]

2021년 2월 17일 (수) 04:43 기준 최신판

개요

  • 사각형 모양의 띠를 가지고, 왼쪽과 오른쪽 양끝을 서로 붙이되 한번 꼬아서 붙인 것을 뫼비우스의 띠라 함.

2014134-moeb.gif

  • 뫼비우스의 띠에서는 곡면의 안과 밖을 구분할 수가 없음.
    • 한 점에서 출발하여 계속 걸어가면, 같은 점에 반대면에 처음에서 거꾸로 선 상태로 도달할수 있고, 계속 걸어간다면, 그 점에 처음 출발할 때의 상태로 돌아올 수 있음.

2014134-escher-mobius-2.jpg

수학을 소재로 한 예술작품을 많이 남긴 에셔의 작품

  • fiber product



재미있는 사실

  • 조세희의 연작 소설 '난장이가 쏘아올린 작은 공'에는 '〈뫼비우스의 띠〉'를 제목으로 하는 이야기가 수록되어 있음.
  • 이렇게 돌고도는 뫼비우스 띠의 성질은, 주변에서 흔히 볼 수 있는 재활용 마크의 디자인에 활용되었음.

2014134-recycle.jpg

  • 직접 뫼비우스의 띠를 만들어 보는 것도 재미있을 것이다. 긴 띠를 한번 꼬아서 풀로 붙이면 된다.
    • 뫼비우스 띠 양 모서리의 중점을 이어서 가위로 자르면 재미있는 일이 벌어진다.
    • ⅓ 점과 ⅔ 점을 가위로 잘라 보는 것도 괜찮을걸? (※ 잘라 보면 알겠지만, 가위질은 한 번이다.)
  • SK 텔레콤의 T로고는 뫼비우스 띠를 모티브로 삼은 것



역사



관련된 고교수학 또는 대학수학



관련된 항목들



관련도서



사전형태의 자료


리뷰, 에세이, 강의노트


관련기사

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'möbius'}, {'LEMMA': 'strip'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=뫼비우스의_띠&oldid=52290"