"카탈란 수 (Catalan numbers)"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
|||
| (사용자 2명의 중간 판 35개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | + | * 조합수학에서 빈번하게 등장하는 수열의 하나 | |
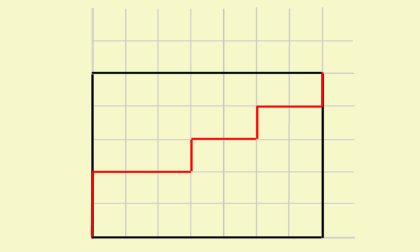
| + | * (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 <math>y=x</math>를 넘지 않는 경우의 수 | ||
| + | * <math>n\geq 0 </math>에 대하여 다음과 같이 주어짐:<math>c_n = \frac{1}{n+1}{2n\choose n} = \frac{(2n)!}{(n+1)!\,n!}</math> | ||
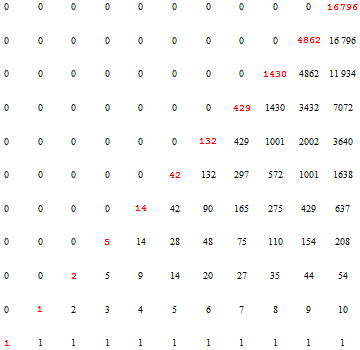
| + | * 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012,… | ||
| − | + | [[파일:카탈란 수열(Catalan numbers)1.png]] | |
| + | |||
| − | + | ||
| − | * | + | ==점화식== |
| − | + | * 다음의 점화식이 성립한다 | |
| + | <math>c_{n+1}=c_0c_n+c_1c_{n-1}+\cdots+c_nc_0 \label{rec}</math> | ||
| + | * [[홀로노믹 수열]] | ||
| + | :<math> | ||
| + | (n+2)c_{n+1}+(-4 n-2)c_{n}=0 | ||
| + | </math> | ||
| + | |||
| − | + | ||
| − | + | ==생성함수== | |
| + | * 기본적인 내용에 대해서는 [[생성함수]] 항목을 참조 | ||
| + | * 카탈란 수열의 생성함수는 다음과 같이 주어짐 | ||
| + | :<math>G(x)= c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots=\frac{1-\sqrt{1-4x}}{2x}</math> | ||
| − | < | + | ===증명=== |
| + | 생성함수를 다음과 같이 두자 | ||
| + | :<math>G(x)= c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots</math> | ||
| + | 다음을 얻을 수 있다 | ||
| + | :<math>x G(x)^2= (c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots)^2=c_0^2x+(c_0c_1+c_1c_0)x^2+(c_0c_2+c_1c_1+c_2c_0)x^3+\cdots=G(x)-1</math> | ||
| + | 여기에 \ref{rec} 을 이용하면, | ||
| + | :<math>x G(x)^2-G(x)+1=0</math> | ||
| + | 따라서 | ||
| + | :<math>G(x)= \frac{1-\sqrt{1-4x}}{2x}</math>■ | ||
| − | + | ||
| − | + | ||
| − | + | ==점근 급수== | |
| + | * 멱급수 <math>(1-x)^{-1/2}=\sum_{n=0}^{\infty} a_n x^n</math>의 계수는 다음과 같은 점근 급수를 갖는다 | ||
| + | :<math> | ||
| + | a_n \sim \frac{1}{\sqrt{\pi n}}\left(1-\frac{1}{8 n}+\frac{1}{128 n^2}+\frac{5}{1024 n^3}+O(\frac{1}{n^4})\right) | ||
| + | </math> | ||
| + | * 카탈란 상수는 다음을 만족한다 | ||
| + | :<math> | ||
| + | c_n=\frac{4^n}{n+1}a_n \sim \frac{4^n}{(n+1)\sqrt{\pi n}}\left(1-\frac{1}{8 n}+\frac{1}{128 n^2}+\frac{5}{1024 n^3}+O(\frac{1}{n^4})\right) | ||
| + | </math> | ||
| + | * [[스털링 공식]] 을 이용하여 다음을 증명할 수 있다 | ||
| + | :<math>c_{n}\sim \frac{4^{n}}{\sqrt{\pi n}(n+1)}(1-\frac{1}{8n})</math> | ||
| + | * [[점근 급수(asymptotic series)]] | ||
| − | + | ||
| − | * (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 | + | ==격자경로와 카탈란 수== |
| − | * (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 <math>y=x</math>를 넘지 않는 경우의 수< | + | ===증명의 아이디어=== |
| + | * (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로의 수 | ||
| + | :<math>{2n \choose n}</math> | ||
| + | * (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 <math>y=x</math>를 넘지 않는 경우의 수 (카탈란 수) | ||
| + | :<math>\frac{1}{n+1}{2n \choose n}</math> | ||
| + | * (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수를 구한 다음, 그 중에서 y=x를 넘어서 가는 방법의 수를 빼면 된다. 이 방법의 수가 얼마가 되겠느냐를 구하는 과정에서 일대일대응이 등장한다. | ||
| − | + | ||
| − | + | ===일단계=== | |
| + | (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수를 구해 보자. 이것은 매우 간단한 문제인데, 일대일대응을 통하여 문제를 풀어보자. 각 경로에서 x축으로 움직이는 것을 X로 표시하고 y축으로 움직이는 것을 Y로 표시하면, 각 경로는 X와Y를 n개 씩 쓴 문자열로 표현된다. 이것이 일대일 대응이다. 각각의 경로는 서로 다른 문자열로 표현될테고, 문자열은 또한 어떤 경로를 표현할테니까 말이다. 따라서 죽 늘어놓은 2n개 중에서 n개를 골라 X라고 써 놓으면 나머지 위치는 Y가 될 것이고 결정될 것이고, 그런 방법의 수는 <math>{2n \choose n}</math>이다. 즉, (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수는 <math>{2n \choose n}</math>이다. | ||
| − | + | ||
| − | + | ===이단계=== | |
| + | 이제 직선 <math>y=x</math>를 넘어서서 가는 경로의 수를 구하자. 경로는 반드시 <math>y=x+1</math>과 만나게 될 것이다. | ||
| − | + | [[파일:카탈란 수열(Catalan numbers)meeting.jpg]] | |
| − | + | 이 때, 이 경로의 <math>(0,0)</math>에서부터 <math>y=x+1</math>과 처음으로 만나는 점까지를 잘라서, <math>y=x</math>에 대칭시키자. | |
| − | ( | + | [[파일:카탈란 수열(Catalan numbers)Symmetrization.jpg]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
그리고 나머지 경로를 평행이동시켜 대칭이동된 경로에 갖다붙이자. | 그리고 나머지 경로를 평행이동시켜 대칭이동된 경로에 갖다붙이자. | ||
| − | + | [[파일:카탈란 수열(Catalan numbers)translation.jpg]] | |
| + | 그 결과는 <math>(0,0)</math>에서 출발하여 <math>(n+1,n-1)</math>에 도착하는 경로일 것이다. | ||
| + | [[파일:카탈란 수열(Catalan numbers)result.jpg]] | ||
| − | + | 위에서 한 작업은 서로 다른 두 경로의 집합 사이에 어떤 대응을 만들어 낸 것이다. 이 대응은 일대일 대응이다. 일대일대응임을 보이기 위해서는 두 가지를 생각해야 한다. 첫번째는, 서로 다른 것으로 대응되었는지를 살피고, 두번째는 공역의 모든 원소가 대응되었는지를 살피는 것이다. | |
| − | + | <math>y=x</math>를 넘어서서 가는 경로는 <math>(0,0)</math>에서 <math>(n+1,n-1)</math>까지 가는 경로와 일대일 대응되므로 그 개수는 <math>{2n \choose n+1}</math>이다. | |
| − | + | 따라서 처음에 제기했던 문제의 답은 다음과 같다 | |
| + | :<math>{2n \choose n}-{2n \choose n+1}=\frac{1}{n+1}{2n \choose n}</math> ■ | ||
| + | |||
| + | |||
| − | + | ||
| − | + | ==적분표현== | |
| − | + | * <math>c_n=\int_{0}^{1} 2^{2n+1}{\cos^{2n} \pi x}\, {\sin^2 \pi x}\,dx</math> | |
| − | |||
| − | |||
| − | + | ==역사== | |
| − | + | * [[수학사 연표]] | |
| + | |||
| + | |||
| − | + | ==메모== | |
| + | * [http://bomber0.byus.net/index.php/2008/05/10/643 일대일대응 그리고 카탈란의 수(Catalan Numbers)] | ||
| − | + | ||
| − | + | ==관련된 항목들== | |
| + | * [[정다각형의 삼각화]] | ||
| + | * [[Dyck 경로]] | ||
| + | * [[Associahedron]] | ||
| + | * [[모츠킨 수 (Motzkin number)]] | ||
| + | * [[격자 경로]] | ||
| + | |||
| − | |||
| − | + | ==매스매티카 파일 및 계산 리소스== | |
| + | * [http://www.research.att.com/%7Enjas/sequences/index.html The On-Line Encyclopedia of Integer Sequences] | ||
| + | ** https://oeis.org/A000108 | ||
| − | + | ||
| − | + | ==사전 형태의 자료== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* http://ko.wikipedia.org/wiki/ | * http://ko.wikipedia.org/wiki/ | ||
* http://en.wikipedia.org/wiki/Catalan_number | * http://en.wikipedia.org/wiki/Catalan_number | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | ==리뷰, 에세이, 강의노트== | ||
| + | * Pak, Igor. “History of Catalan Numbers.” arXiv:1408.5711 [math], August 25, 2014. http://arxiv.org/abs/1408.5711. | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | ==관련도서== | |
| − | + | * Thomas Koshy [http://www.amazon.com/exec/obidos/ASIN/019533454X/ref=nosim/addallbooksearch Catalan Numbers with Applications], Oxford University Press, USA, 2008 | |
| − | + | [[분류:조합수학]] | |
| + | [[분류:수열]] | ||
| − | + | ==메타데이터== | |
| − | + | ===위키데이터=== | |
| − | * | + | * ID : [https://www.wikidata.org/wiki/Q270513 Q270513] |
| − | + | ===Spacy 패턴 목록=== | |
| − | + | * [{'LOWER': 'catalan'}, {'LEMMA': 'number'}] | |
| − | * [ | ||
2021년 2월 17일 (수) 05:01 기준 최신판
개요
- 조합수학에서 빈번하게 등장하는 수열의 하나
- (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 \(y=x\)를 넘지 않는 경우의 수
- \(n\geq 0 \)에 대하여 다음과 같이 주어짐\[c_n = \frac{1}{n+1}{2n\choose n} = \frac{(2n)!}{(n+1)!\,n!}\]
- 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012,…
점화식
- 다음의 점화식이 성립한다
\(c_{n+1}=c_0c_n+c_1c_{n-1}+\cdots+c_nc_0 \label{rec}\)
\[ (n+2)c_{n+1}+(-4 n-2)c_{n}=0 \]
생성함수
- 기본적인 내용에 대해서는 생성함수 항목을 참조
- 카탈란 수열의 생성함수는 다음과 같이 주어짐
\[G(x)= c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots=\frac{1-\sqrt{1-4x}}{2x}\]
증명
생성함수를 다음과 같이 두자 \[G(x)= c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots\] 다음을 얻을 수 있다 \[x G(x)^2= (c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n + \cdots)^2=c_0^2x+(c_0c_1+c_1c_0)x^2+(c_0c_2+c_1c_1+c_2c_0)x^3+\cdots=G(x)-1\] 여기에 \ref{rec} 을 이용하면, \[x G(x)^2-G(x)+1=0\] 따라서 \[G(x)= \frac{1-\sqrt{1-4x}}{2x}\]■
점근 급수
- 멱급수 \((1-x)^{-1/2}=\sum_{n=0}^{\infty} a_n x^n\)의 계수는 다음과 같은 점근 급수를 갖는다
\[ a_n \sim \frac{1}{\sqrt{\pi n}}\left(1-\frac{1}{8 n}+\frac{1}{128 n^2}+\frac{5}{1024 n^3}+O(\frac{1}{n^4})\right) \]
- 카탈란 상수는 다음을 만족한다
\[ c_n=\frac{4^n}{n+1}a_n \sim \frac{4^n}{(n+1)\sqrt{\pi n}}\left(1-\frac{1}{8 n}+\frac{1}{128 n^2}+\frac{5}{1024 n^3}+O(\frac{1}{n^4})\right) \]
- 스털링 공식 을 이용하여 다음을 증명할 수 있다
\[c_{n}\sim \frac{4^{n}}{\sqrt{\pi n}(n+1)}(1-\frac{1}{8n})\]
격자경로와 카탈란 수
증명의 아이디어
- (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로의 수
\[{2n \choose n}\]
- (0,0)에서 (n,n)까지 격자점을 지나는 최단거리의 경로 중에서 직선 \(y=x\)를 넘지 않는 경우의 수 (카탈란 수)
\[\frac{1}{n+1}{2n \choose n}\]
- (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수를 구한 다음, 그 중에서 y=x를 넘어서 가는 방법의 수를 빼면 된다. 이 방법의 수가 얼마가 되겠느냐를 구하는 과정에서 일대일대응이 등장한다.
일단계
(0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수를 구해 보자. 이것은 매우 간단한 문제인데, 일대일대응을 통하여 문제를 풀어보자. 각 경로에서 x축으로 움직이는 것을 X로 표시하고 y축으로 움직이는 것을 Y로 표시하면, 각 경로는 X와Y를 n개 씩 쓴 문자열로 표현된다. 이것이 일대일 대응이다. 각각의 경로는 서로 다른 문자열로 표현될테고, 문자열은 또한 어떤 경로를 표현할테니까 말이다. 따라서 죽 늘어놓은 2n개 중에서 n개를 골라 X라고 써 놓으면 나머지 위치는 Y가 될 것이고 결정될 것이고, 그런 방법의 수는 \({2n \choose n}\)이다. 즉, (0,0)에서 (n,n)까지 갈 수 있는 모든 방법의 수는 \({2n \choose n}\)이다.
이단계
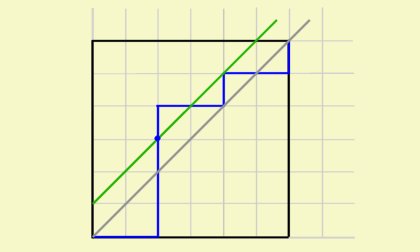
이제 직선 \(y=x\)를 넘어서서 가는 경로의 수를 구하자. 경로는 반드시 \(y=x+1\)과 만나게 될 것이다.
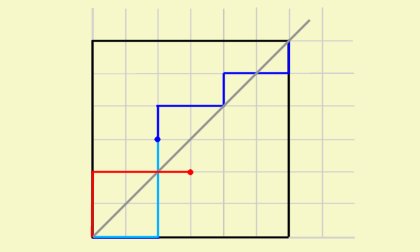
이 때, 이 경로의 \((0,0)\)에서부터 \(y=x+1\)과 처음으로 만나는 점까지를 잘라서, \(y=x\)에 대칭시키자.
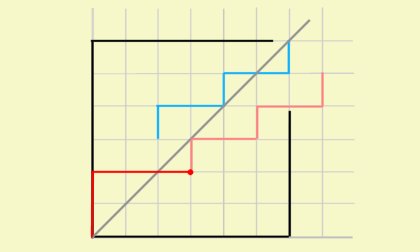
그리고 나머지 경로를 평행이동시켜 대칭이동된 경로에 갖다붙이자.
그 결과는 \((0,0)\)에서 출발하여 \((n+1,n-1)\)에 도착하는 경로일 것이다.
위에서 한 작업은 서로 다른 두 경로의 집합 사이에 어떤 대응을 만들어 낸 것이다. 이 대응은 일대일 대응이다. 일대일대응임을 보이기 위해서는 두 가지를 생각해야 한다. 첫번째는, 서로 다른 것으로 대응되었는지를 살피고, 두번째는 공역의 모든 원소가 대응되었는지를 살피는 것이다.
\(y=x\)를 넘어서서 가는 경로는 \((0,0)\)에서 \((n+1,n-1)\)까지 가는 경로와 일대일 대응되므로 그 개수는 \({2n \choose n+1}\)이다.
따라서 처음에 제기했던 문제의 답은 다음과 같다 \[{2n \choose n}-{2n \choose n+1}=\frac{1}{n+1}{2n \choose n}\] ■
적분표현
- \(c_n=\int_{0}^{1} 2^{2n+1}{\cos^{2n} \pi x}\, {\sin^2 \pi x}\,dx\)
역사
메모
관련된 항목들
매스매티카 파일 및 계산 리소스
사전 형태의 자료
리뷰, 에세이, 강의노트
- Pak, Igor. “History of Catalan Numbers.” arXiv:1408.5711 [math], August 25, 2014. http://arxiv.org/abs/1408.5711.
관련도서
- Thomas Koshy Catalan Numbers with Applications, Oxford University Press, USA, 2008
메타데이터
위키데이터
- ID : Q270513
Spacy 패턴 목록
- [{'LOWER': 'catalan'}, {'LEMMA': 'number'}]