"패리 수열(Farey series)"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
(피타고라스님이 이 페이지에 Farey_Sequence.png 파일을 등록하셨습니다.)
 
(사용자 3명의 중간 판 43개는 보이지 않습니다)
1번째 줄: 1번째 줄:
 +
==개요==
  
 +
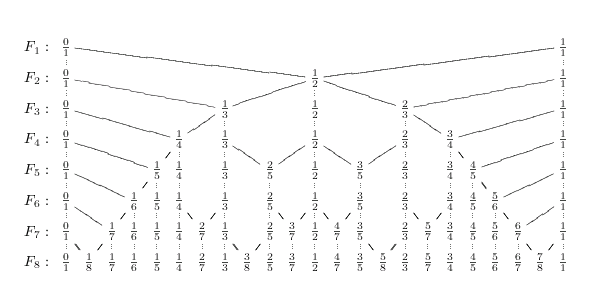
*  Fn 은 0부터 1사이의 분모가 n이하인 기약분수의 집합
 +
** F1 = {0⁄1, 1⁄1}
 +
** F2 = {0⁄1, 1⁄2, 1⁄1}
 +
** F3 = {0⁄1, 1⁄3, 1⁄2, 2⁄3, 1⁄1}
 +
** F4 = {0⁄1, 1⁄4, 1⁄3, 1⁄2, 2⁄3, 3⁄4, 1⁄1}
 +
** F5 = {0⁄1, 1⁄5, 1⁄4, 1⁄3, 2⁄5, 1⁄2, 3⁄5, 2⁄3, 3⁄4, 4⁄5, 1⁄1}
 +
** F6 = {0⁄1, 1⁄6, 1⁄5, 1⁄4, 1⁄3, 2⁄5, 1⁄2, 3⁄5, 2⁄3, 3⁄4, 4⁄5, 5⁄6, 1⁄1} 
 +
** F7 = {0⁄1, 1⁄7, 1⁄6, 1/5, 1/4, 2/7, 1⁄3, 2⁄5, 3⁄7, 1⁄2, 4⁄7, 3⁄5, 2⁄3, 5⁄7, 3⁄4, 4⁄5, 5⁄6, 6⁄7, 1⁄1}
 +
 +
[[파일:1984310-Farey_Sequence(1).png]]
 +
 +
*  두 분수에 대해 '초딩들의 꿈의 분수덧셈'을 다음과 같이 정의하면,:<math>\frac{a}{b}\oplus\frac{c}{d}=\frac{a+c}{b+d}</math>
 +
 +
*  주어진 order의 Farey series에 등장하는 연속된 세 수를 보면, 가운데 수는 언제나 그 옆에 있는 두 수의 ‘초딩들의 꿈의 분수덧셈’을 통해서 얻어지는 것을 관찰할 수 있다.
 +
** 이 관찰의 증명은 맨 아래의 '참고할만한 자료'에서 찾을 수 있음
 +
 +
 +
 +
 +
 +
==인접합 두 수가 만족하는 성질==
 +
* <math>F_n</math>의 인접한 두 분수, <math>\frac{b}{a} < \frac{d}{c}</math> 사이에는 다음과 같은 관계가 성립
 +
:<math>ad-bc=1</math>
 +
 +
 +
 +
 +
 +
오늘은 이것을 증명한다. 이것을 증명하면, 초딩들의 꿈의 분수덧셈이 왜 참인지 쉽게 알 수 있다.
 +
 +
 +
 +
이제 문제를 기하학적으로 해석해 보자. F5 = {0⁄1, 1⁄5, 1⁄4, 1⁄3, 2⁄5, 1⁄2, 3⁄5, 2⁄3, 3⁄4, 4⁄5, 1⁄1} 를 예를 들어 설명한다.
 +
 +
 +
 +
먼저 각각의 분수들에 대해, 좌표평면에다가 다음과 같은 방식의 대응관계를 찾아 점을 찍는다. 즉,
 +
:<math>
 +
0/1 \mapsto (1,0)\\
 +
1/5 \mapsto (5,1)\\
 +
1/4 \mapsto (4,1)\\
 +
\cdots \\
 +
3/4 \mapsto (4,3)\\
 +
4/5 \mapsto (5,4)\\
 +
1/1 \mapsto (1,1)\\
 +
</math>
 +
 +
 +
그러면 아래와 같은 그림이 얻어진다.
 +
 +
 +
 +
 +
 +
 +
 +
이 다음 각각의 좌표를 원점과 잇는 선분을 그린다.
 +
 +
 +
 +
 +
 +
 +
 +
각각의 분수들은 이와 같이 얻어진 직선의 기울기와 같다는 것을 알 수 있다. 인접한 두 분수는 인접한 두 직선으로 나타나고 있다.
 +
 +
 +
 +
이제 왜 인접한 <math>\frac{b}{a} < \frac{d}{c}</math>, 가 <math>ad-bc=1</math>를 만족시키는가를 이해해 보자. 예를 들어, 1/2와 3/5는 인접해 있는데, 2×3-1×5=1을 만족시키고 있다. 이 상황을 기하학적으로 이해하자.
 +
 +
 +
 +
좌표평면 상에서 (0,0), (a,b), (c,d)이 그리는 격자삼각형을 생각해보자. ( (0,0),(2,1), (5,3) 의 경우를 구체적으로 생각해보라)
 +
 +
 +
 +
'''세 점을 이어서 삼각형을 그리게 되면, 이 삼각형은 그 내부와 경계에 (0,0), (a,b), (c,d)를 제외한 다른 격자들을 가지고 있지 않다.''' 이 관찰이 매우 중요하므로, 이것이 왜 참인지, <math>F_n</math>의 정의를 가지고 곰곰이 생각해보면 좋겠다.
 +
 +
 +
 +
이제 [[픽의 정리(Pick's Theorem)]]에 의해, 삼각형의 넓이는 <math>\frac{1}{2}</math>가 된다. (I=0,B=3 인 경우) 픽의 정리는
 +
 +
 +
 +
 +
 +
 +
를 말한다.한편 좌표평면 상에, 원점과 (a,b), (c,d) 세 점이 결정하는 삼각형의 넓이는 다음과 같이 주어진다.
 +
:<math>\frac{|ad-bc|}{2}</math>
 +
따라서 ad-bc가 양수라면, ad-bc=1이 성립해야만 한다.
 +
 +
 +
==패리 산수==
 +
 +
<blockquote>
 +
<math>\frac{a}{b}\oplus\frac{c}{d}=\frac{a+c}{b+d}</math>
 +
</blockquote>
 +
 +
이제 목표했던 대로,
 +
 +
<blockquote>
 +
주어진 order의 Farey series에 등장하는 연속된 세 수를 보면, 가운데 수는 언제나 그 옆에 있는 두 수의 ‘초딩들의 꿈의 분수덧셈’을 통해서 얻어진다.
 +
</blockquote>
 +
 +
를 증명한다. 지난 번 글에서는 다음 결과를 증명했다.
 +
 +
<blockquote>
 +
<math>F_n</math>의 인접한 두 분수,
 +
 +
<math>\frac{b}{a} < \frac{d}{c}</math>
 +
 +
사이에는 다음과 같은 관계가 성립한다.
 +
 +
<math>ad-bc=1</math>
 +
</blockquote>
 +
 +
이제 이 결과를 이용해서, 초딩들의 꿈이 왜 참이 되는지를 증명한다.
 +
 +
<math>F_n</math>의 인접한 세 수를
 +
 +
<blockquote>
 +
<math>\frac{b}{a} <\frac{x}{y} < \frac{d}{c}</math>
 +
</blockquote>
 +
 +
라고 하면, 다음 식들을 얻게 된다.
 +
 +
<blockquote>
 +
<math>ax-by=1</math>:<math>dy-bx=1</math>
 +
</blockquote>
 +
 +
두 식을 서로 뺀다.
 +
 +
<blockquote>
 +
<math>(ax-by)-(dy-cx)=0</math>
 +
</blockquote>
 +
 +
즉
 +
 +
<blockquote>
 +
<math>(a+c)x-(b+d)y=0</math>
 +
</blockquote>
 +
 +
따라서,
 +
 +
<blockquote>
 +
<math>\frac{x}{y}=\frac{b+d}{a+c}</math>
 +
</blockquote>
 +
 +
따라서 초딩들의 꿈의 덧셈은 참이다.
 +
 +
;주의
 +
분수덧셈 배우는 초딩들 헷갈리는 사태가 발생할 수 있으므로, 초등학교에서는 교육을 권장하지 않음
 +
 +
 +
 +
==F_n의 크기==
 +
 +
 +
 +
 +
 +
==메모==
 +
 +
* http://www3.telus.net/ldh/math/farey_hurwitz.pdf
 +
* http://scimath.unl.edu/MIM/files/MATExamFiles/AmenGreenSchmidt_MAT_Exam_Expository%20Paper.pdf
 +
 +
 +
 +
 +
 +
==관련된 단원==
 +
*  정수
 +
** 약수와 배수
 +
** 서로소
 +
 +
 +
 +
==관련된 항목들==
 +
 +
* [[픽의 정리(Pick's Theorem)]]
 +
* [[포드 원 (Ford Circles)]]
 +
* [[콕세터 프리즈]]
 +
 +
 +
 +
 +
 +
==관련된 대학 수학==
 +
 +
* [[초등정수론]]
 +
* [[추상대수학]]
 +
** 유한체 - Freshman's dream
 +
* [[모듈라 군, j-invariant and the singular moduli|The modular group, j-invariant and the singular moduli]]
 +
** [[모듈라 군(modular group)|modular group]]
 +
 +
 +
 +
 +
 +
==매스매티카 파일 및 계산 리소스==
 +
 +
* https://docs.google.com/file/d/0B8XXo8Tve1cxYmI3ZWJkNDItYWNiZi00OThlLTg4NTYtNTkzNWNiY2U0NmFk/edit
 +
 +
 +
 +
==사전 형태의 자료==
 +
* http://en.wikipedia.org/wiki/John_Farey,_Sr.
 +
 +
==관련논문==
 +
* Short, Ian, and Mairi Walker. “Even-Integer Continued Fractions and the Farey Tree.” arXiv:1508.01373 [math], August 6, 2015. http://arxiv.org/abs/1508.01373.
 +
* Lagarias, Jeffery, and Harsh Mehta. ‘Products of Farey Fractions’. arXiv:1503.00199 [math], 28 February 2015. http://arxiv.org/abs/1503.00199.
 +
* Neville, E. H. 1949. “The structure of Farey series”. <em>Proceedings of the London Mathematical Society. Second Series</em> 51: 132–144.
 +
 +
 +
 +
 +
 +
==블로그==
 +
* [http://bomber0.byus.net/index.php/2008/04/18/594 초딩들의 꿈 - Farey Series] (피타고라스의 창)
 +
* [http://bomber0.byus.net/index.php/2008/04/23/613 초딩들의 꿈 - Farey Series (2)] (피타고라스의 창)
 +
* [http://bomber0.byus.net/index.php/2008/05/08/642 초딩들의 꿈 - Farey Series (3)] (피타고라스의 창)
 +
* [http://bomber0.byus.net/index.php/2008/07/28/698 오늘의 퀴즈 : Farey series의 크기]
 +
** 피타고라스의 창, 2008-7-28
 +
 +
 +
 +
==더 읽을 거리==
 +
 +
* [http://navercast.naver.com/science/math/1049 바보셈에서 페리수열]
 +
** 네이버 오늘의 과학, 2009년 9월 8일, 이광연
 +
[[분류:정수론]]
 +
[[분류:수열]]
 +
 +
==메타데이터==
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q355803 Q355803]
 +
===Spacy 패턴 목록===
 +
* [{'LOWER': 'john'}, {'LEMMA': 'Farey'}]

2021년 2월 17일 (수) 05:05 기준 최신판

개요

  • Fn 은 0부터 1사이의 분모가 n이하인 기약분수의 집합
    • F1 = {0⁄1, 1⁄1}
    • F2 = {0⁄1, 1⁄2, 1⁄1}
    • F3 = {0⁄1, 1⁄3, 1⁄2, 2⁄3, 1⁄1}
    • F4 = {0⁄1, 1⁄4, 1⁄3, 1⁄2, 2⁄3, 3⁄4, 1⁄1}
    • F5 = {0⁄1, 1⁄5, 1⁄4, 1⁄3, 2⁄5, 1⁄2, 3⁄5, 2⁄3, 3⁄4, 4⁄5, 1⁄1}
    • F6 = {0⁄1, 1⁄6, 1⁄5, 1⁄4, 1⁄3, 2⁄5, 1⁄2, 3⁄5, 2⁄3, 3⁄4, 4⁄5, 5⁄6, 1⁄1}
    • F7 = {0⁄1, 1⁄7, 1⁄6, 1/5, 1/4, 2/7, 1⁄3, 2⁄5, 3⁄7, 1⁄2, 4⁄7, 3⁄5, 2⁄3, 5⁄7, 3⁄4, 4⁄5, 5⁄6, 6⁄7, 1⁄1}

1984310-Farey Sequence(1).png

  • 두 분수에 대해 '초딩들의 꿈의 분수덧셈'을 다음과 같이 정의하면,\[\frac{a}{b}\oplus\frac{c}{d}=\frac{a+c}{b+d}\]
  • 주어진 order의 Farey series에 등장하는 연속된 세 수를 보면, 가운데 수는 언제나 그 옆에 있는 두 수의 ‘초딩들의 꿈의 분수덧셈’을 통해서 얻어지는 것을 관찰할 수 있다.
    • 이 관찰의 증명은 맨 아래의 '참고할만한 자료'에서 찾을 수 있음



인접합 두 수가 만족하는 성질

  • \(F_n\)의 인접한 두 분수, \(\frac{b}{a} < \frac{d}{c}\) 사이에는 다음과 같은 관계가 성립

\[ad-bc=1\]



오늘은 이것을 증명한다. 이것을 증명하면, 초딩들의 꿈의 분수덧셈이 왜 참인지 쉽게 알 수 있다.


이제 문제를 기하학적으로 해석해 보자. F5 = {0⁄1, 1⁄5, 1⁄4, 1⁄3, 2⁄5, 1⁄2, 3⁄5, 2⁄3, 3⁄4, 4⁄5, 1⁄1} 를 예를 들어 설명한다.


먼저 각각의 분수들에 대해, 좌표평면에다가 다음과 같은 방식의 대응관계를 찾아 점을 찍는다. 즉, \[ 0/1 \mapsto (1,0)\\ 1/5 \mapsto (5,1)\\ 1/4 \mapsto (4,1)\\ \cdots \\ 3/4 \mapsto (4,3)\\ 4/5 \mapsto (5,4)\\ 1/1 \mapsto (1,1)\\ \]


그러면 아래와 같은 그림이 얻어진다.




이 다음 각각의 좌표를 원점과 잇는 선분을 그린다.




각각의 분수들은 이와 같이 얻어진 직선의 기울기와 같다는 것을 알 수 있다. 인접한 두 분수는 인접한 두 직선으로 나타나고 있다.


이제 왜 인접한 \(\frac{b}{a} < \frac{d}{c}\), 가 \(ad-bc=1\)를 만족시키는가를 이해해 보자. 예를 들어, 1/2와 3/5는 인접해 있는데, 2×3-1×5=1을 만족시키고 있다. 이 상황을 기하학적으로 이해하자.


좌표평면 상에서 (0,0), (a,b), (c,d)이 그리는 격자삼각형을 생각해보자. ( (0,0),(2,1), (5,3) 의 경우를 구체적으로 생각해보라)


세 점을 이어서 삼각형을 그리게 되면, 이 삼각형은 그 내부와 경계에 (0,0), (a,b), (c,d)를 제외한 다른 격자들을 가지고 있지 않다. 이 관찰이 매우 중요하므로, 이것이 왜 참인지, \(F_n\)의 정의를 가지고 곰곰이 생각해보면 좋겠다.


이제 픽의 정리(Pick's Theorem)에 의해, 삼각형의 넓이는 \(\frac{1}{2}\)가 된다. (I=0,B=3 인 경우) 픽의 정리는




를 말한다.한편 좌표평면 상에, 원점과 (a,b), (c,d) 세 점이 결정하는 삼각형의 넓이는 다음과 같이 주어진다. \[\frac{|ad-bc|}{2}\] 따라서 ad-bc가 양수라면, ad-bc=1이 성립해야만 한다.


패리 산수

\(\frac{a}{b}\oplus\frac{c}{d}=\frac{a+c}{b+d}\)

이제 목표했던 대로,

주어진 order의 Farey series에 등장하는 연속된 세 수를 보면, 가운데 수는 언제나 그 옆에 있는 두 수의 ‘초딩들의 꿈의 분수덧셈’을 통해서 얻어진다.

를 증명한다. 지난 번 글에서는 다음 결과를 증명했다.

\(F_n\)의 인접한 두 분수,

\(\frac{b}{a} < \frac{d}{c}\)

사이에는 다음과 같은 관계가 성립한다.

\(ad-bc=1\)

이제 이 결과를 이용해서, 초딩들의 꿈이 왜 참이 되는지를 증명한다.

\(F_n\)의 인접한 세 수를

\(\frac{b}{a} <\frac{x}{y} < \frac{d}{c}\)

라고 하면, 다음 식들을 얻게 된다.

\(ax-by=1\)\[dy-bx=1\]

두 식을 서로 뺀다.

\((ax-by)-(dy-cx)=0\)

즉

\((a+c)x-(b+d)y=0\)

따라서,

\(\frac{x}{y}=\frac{b+d}{a+c}\)

따라서 초딩들의 꿈의 덧셈은 참이다.

주의

분수덧셈 배우는 초딩들 헷갈리는 사태가 발생할 수 있으므로, 초등학교에서는 교육을 권장하지 않음


F_n의 크기

메모



관련된 단원

  • 정수
    • 약수와 배수
    • 서로소


관련된 항목들



관련된 대학 수학



매스매티카 파일 및 계산 리소스


사전 형태의 자료

관련논문

  • Short, Ian, and Mairi Walker. “Even-Integer Continued Fractions and the Farey Tree.” arXiv:1508.01373 [math], August 6, 2015. http://arxiv.org/abs/1508.01373.
  • Lagarias, Jeffery, and Harsh Mehta. ‘Products of Farey Fractions’. arXiv:1503.00199 [math], 28 February 2015. http://arxiv.org/abs/1503.00199.
  • Neville, E. H. 1949. “The structure of Farey series”. Proceedings of the London Mathematical Society. Second Series 51: 132–144.



블로그


더 읽을 거리

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'john'}, {'LEMMA': 'Farey'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=패리_수열(Farey_series)&oldid=52525"